矩阵的LU分解法——Python实现
理论参考:
LU分解、LDLT分解和Cholesky分解 https://blog.csdn.net/zhouliyang1990/article/details/21952485
Doolittle分解法(LU分解)详细分析以及matlab的实现 https://blog.csdn.net/lol_IP/article/details/78491457
在线性代数中,LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积)。LU分解主要应用在数值分析中,用来解线性方程、求反矩阵或计算行列式。
LU分解在本质上是高斯消元法的一种表达形式。实质上是将A通过初等行变换变成一个上三角矩阵,其变换矩阵就是一个单位下三角矩阵。这正是所谓的杜尔里特算法(Doolittle algorithm):从下至上地对矩阵A做初等行变换,将对角线左下方的元素变成零,然后再证明这些行变换的效果等同于左乘一系列单位下三角矩阵,这一系列单位下三角矩阵的乘积的逆就是L矩阵,它也是一个单位下三角矩阵。这类算法的复杂度一般在(三分之二的n三次方) 左右。
伪代码:
算法 LU Decomposition
//输入矩阵A[1…n,1…n],并且A的所有顺序主子式都不为0
//输出下三角矩阵L和上三角矩阵U
L←n阶zero矩阵 //初始化一个n阶zero矩阵
U←n阶zero矩阵
for i ← 1 to n do
L[i][i] ← 1 //L的主对角线元素全为1
if i==0 do //分别利用A的第一行元素第一列元素,确定L的第一列元素和U的第一行元素
U[0][0] ← A[0][0]
for j ← 1 to n do
U[0][j] ←A[0][j]
L[j][0] ←A[j][0]/U[0][0]
else
for j ← i to n do //计算矩阵U
for k ← 1 to i-1 do
temp ←L[i][k] * U[k][j]
U[i][j] ←A[i][j]-temp
for j ← i+1 to n do //计算矩阵L
for k ← 1 to i-1 do
temp ←L[j][k] * U[k][i]
L[j][i] ← (A[j][i] - temp)/U[i][i]
代码实现:
import numpy as np
import pandas as pd
np.random.seed(2)
def LU_decomposition(A):
n=len(A[0])
L = np.zeros([n,n])
U = np.zeros([n, n])
for i in range(n):
L[i][i]=1
if i==0:
U[0][0] = A[0][0]
for j in range(1,n):
U[0][j]=A[0][j]
L[j][0]=A[j][0]/U[0][0]
else:
for j in range(i, n):#U
temp=0
for k in range(0, i):
temp = temp+L[i][k] * U[k][j]
U[i][j]=A[i][j]-temp
for j in range(i+1, n):#L
temp = 0
for k in range(0, i ):
temp = temp + L[j][k] * U[k][i]
L[j][i] = (A[j][i] - temp)/U[i][i]
return L,U
if __name__ == '__main__':
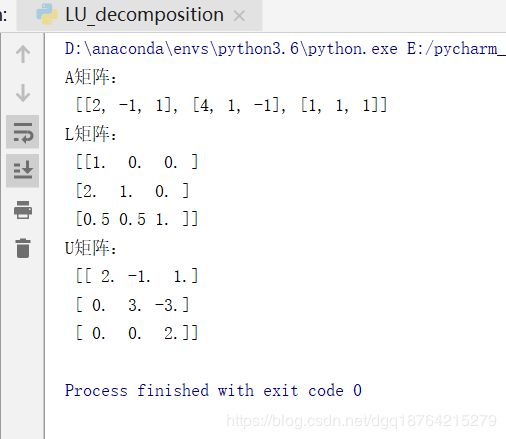
#A=np.random.randint(1,10,size=[3,3]) #注意A的顺序主子式大于零
A=[[2,-1,1],[4,1,-1],[1,1,1]] #举一个例子
L,U=LU_decomposition(A)
print(L,'\n',U)实验结果:
改进1:
在相同的输入情况下,LU分解法比Gauss消去法、列主元素消去法两者效率更高。因为一旦得到了LU矩阵无论右边是什么样的B向量,都可以用AX=B来求解。同时LU分解不是非得需要额外的存储空间,我们把U的非零部分存储到A的上三角部分,把L的非零部分存储到A的下三角部分,可以如下:
import numpy as np
import pandas as pd
def LU_decomposition(A):
n=len(A[0])
for i in range(n):
if i==0:
for j in range(1,n):
A[j][0]=A[j][0]/A[0][0]
else:
for j in range(i, n):#U
temp=0
for k in range(0, i):
temp = temp+A[i][k] * A[k][j]
A[i][j]=A[i][j]-temp
for j in range(i+1, n):#L
temp = 0
for k in range(0, i ):
temp = temp + A[j][k] * A[k][i]
A[j][i] = (A[j][i] - temp)/A[i][i]
return A
if __name__ == '__main__':
#A=np.random.randint(1,10,size=[3,3])
A=[[2,-1,1],[4,1,-1],[1,1,1]]
A=LU_decomposition(A)
print(A)但是,上面并没有给出LU分解的前提,也就是当n阶矩阵A的顺序主子式都非零的时候存在唯一的Doolittle分解,如果出现顺序主子式为零的时候则会出错,如下:
因此在此之前应该对A的顺序主子式进行判别。最终版完整代码如下:
import numpy as np
import pandas as pd
#np.random.seed(2)
def det(A): #求A的行列式
if len(A) <= 0:
return None
elif len(A) == 1:
return A[0][0]
else:
s = 0
for i in range(len(A)):
n = [[row[a] for a in range(len(A)) if a != i] for row in A[1:]] # 这里生成余子式
s += A[0][i] * det(n) * (-1) ** (i )
return s
def Master_Sequential(A,n): #判断A的k阶顺序主子式是否非零,非零满足LU分解的条件
for i in range(0,n):
Master = np.zeros([i+1,i+1])
for row in range(0,i+1):
for a in range(0,i+1):
Master[row][a]=A[row][a]
if det(Master)==0:
done=False
return done
def LU_decomposition(A):
n=len(A[0])
L = np.zeros([n,n])
U = np.zeros([n, n])
for i in range(n):
L[i][i]=1
if i==0:
U[0][0] = A[0][0]
for j in range(1,n):
U[0][j]=A[0][j]
L[j][0]=A[j][0]/U[0][0]
else:
for j in range(i, n):#U
temp=0
for k in range(0, i):
temp = temp+L[i][k] * U[k][j]
U[i][j]=A[i][j]-temp
for j in range(i+1, n):#L
temp = 0
for k in range(0, i ):
temp = temp + L[j][k] * U[k][i]
L[j][i] = (A[j][i] - temp)/U[i][i]
return L,U
if __name__ == '__main__':
n=3
#A=[[2,-1,1],[4,1,-1],[1,1,1]]
#A = np.random.randint(1, 10, size=[n, n])
A=[[5,9,3],[5,9,1],[5,1,9]]
print('A矩阵:\n',A)
if Master_Sequential(A,n) != False:
L,U=LU_decomposition(A)
print('L矩阵:\n',L, '\nU矩阵:\n',U)
else:
print('A的k阶主子式不全非零,不满足LU分解条件。')
本文来自CSDN博客,转载请标明出处:https://blog.csdn.net/dgq18764215279/article/details/89201238