Gym - 101492I- Protecting the Great Wall 费用流
I - Protecting the Great Wall
China has a very rich history, with written records since 1,500BC. One of the cities that contributes a lot to this history is the capital city of Peking. It is visited yearly by many tourists seeking to get to places such as the Temple of Heaven, the Lugou Bridge, the Yinshan Pagoda Forest, or the Forbidden City. One of the most imposing tourist attractions is the Great Wall, for its history and sheer size.
Peking will host the ACM ICPC World Finals 2018, and one of the chosen group activities is to visit the Great Wall. The event organizers in China want to make these one of the best World Finals ever. They have been planning activities with great care for the safety of all participants throughout the city. For this reason, they charged Marcel "the optimizer" Saito with the job of securing the visit to the Great Wall.
The organizers can hire agents from N security teams, numbered from 1 to N. They may hire any number of agents (possibly none) from each team. The organizers assigned each of these teams a security value, that is, each agent in the i-th team adds Bi points to the security score. Marcel's goal is to come up with a hiring plan for agents so as to maximize the total security score, which is the sum of the security values of the hired agents.
On the other hand, the organizers informed Marcel that each group has its special workflow which may cause conflicts. For this reason, the hiring plan must satisfy a set of M constraints. The j-th constraint is defined by three integers Lj, Rj, and Cj, with the following meaning: the sum of the number of agents hired from the teams from Lj to Rj must be no more than Cj.
Now Marcel has all the data to find an optimal hiring plan and keep his reputable epithet. This looks like an interesting problem, so we want you to solve it as well.
input
The first line contains two integers, N and M. The second line has N integers, B1, B2, ..., BN, where Bi is the security value of the agents in the i-th group. The next M lines contain information about each one of the constraints. The j-th of these M lines contains three integers, Lj, Rj, and Cj. Consider that each team appears in at least one of the M constraints.
1 ≤ N ≤ 200.
1 ≤ M ≤ 4000.
0 ≤ Bi ≤ 2000.
1 ≤ Lj ≤ Rj ≤ N.
0 ≤ Cj ≤ 106.
1 ≤ M ≤ 4000.
0 ≤ Bi ≤ 2000.
1 ≤ Lj ≤ Rj ≤ N.
0 ≤ Cj ≤ 106.
example
Input
4 5
5 12 10 6
2 4 1
1 4 1
3 4 1
1 1 1
1 2 1
4 5
5 12 10 6
2 4 1
1 4 1
3 4 1
1 1 1
1 2 1
Output
12
12
题意:
给你N个数,M个限制,L,R,C,意思是在【L,R】内最多拿C个数,问你满足所有限制,我可以拿到的最大的价值。
思路:
其实这题我和我队友在比赛中是没有看的,因为卡题了,emmmm。对于这题首先想到的是区间dp,确实有大佬是用区间dp做的,但是我不会。太菜了!其实也还可以用网络流的思想做,说到网络流关键就是建图,怎么建图呢?
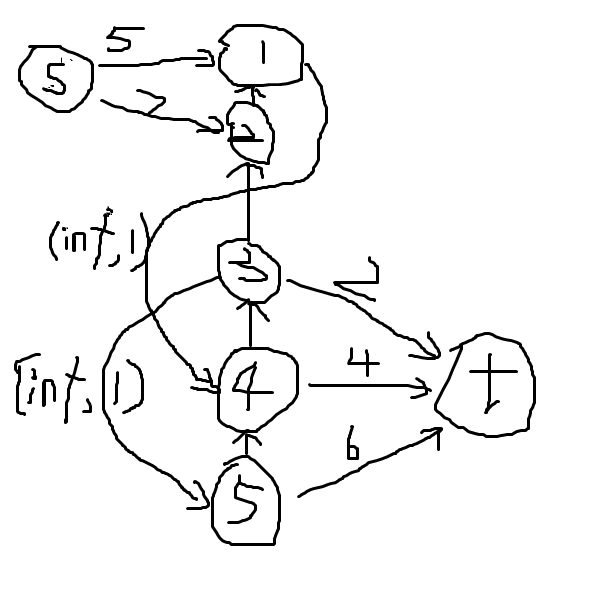
给一组数据:
4 2
5 12 10 6
1 3 1
3 4 1
说明一下,没有标费用的边费用都是0,没有标流量的边流量都是inf。
建完跑一下发现就是答案~~~,更详细的请看代码注释。
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define inf 0x3f3f3f3f
typedef long long ll;
using namespace std;
const int maxn=300;
const int maxm=10005;
struct node
{
int t,f,c,next;
}e[maxm*2];
int a[maxn];
int head[maxn],dis[maxn],vis[maxn];
int pre[maxn];
int cnt,s,t;
void add(int s,int t,int c,int f)
{
e[cnt].t=t;
e[cnt].c=c;
e[cnt].f=f;
e[cnt].next=head[s];
head[s]=cnt++;
e[cnt].t=s;
e[cnt].c=0;
e[cnt].f=-f;
e[cnt].next=head[t];
head[t]=cnt++;
}
void intt()
{
cnt=0;
s=0;t=250;
memset(head,-1,sizeof(head));
}
int spfa()
{
queueque;
for(int i=0;i0&&dis[u]+e[i].f=2;i--)
//多源汇点建图方法
add(i,i-1,inf,0);
for(int i=n+1;i>=1;i--)
{
int temp=a[i]-a[i-1];
if(temp<0)
{
add(i,t,-temp,0);
}
else add(s,i,temp,0);
/*利用差分的思路从最后一个点建图,如果大于0连源点,小于0连汇点*/
}
printf("%lld\n",mincost());
}
还有一个要注意的,一定要是所有点都要被覆盖(题目已经保证了),保证整幅图的连通性,如果这个点没有被覆盖就不能连这条边,连了答案就错了。