SLAM特指:特指搭载传感器的主体,在没有环境先验的信息情况下,在运动过程中建立环境模型,通过估计自己的运动。
SLAM的目的是解决两个问题:1、定位 2、地图构建
也就是说,要一边估计出传感器自身的位置,一边要建立周围环境的模型
最终的目标:实时地,在没有先验知识的情况下进行定位和地图重建。
当相机作为传感器的时候,我们要做的就是根据一张张连续运动的图像,从中估计出相机的运动以及周围环境中的情况
需要大体了解的书籍:
1、概率机器人
2、计算机视觉中的多视图几何
3、机器人学中的状态估计
需要用的Eigen、Opencv、PCL、g2o、Ceres
安装Kdevelop
http://blog.163.com/beichen2012@126/blog/static/16793820820122224332943/
一些常见的传感器



单目(Monocular)、双目(Stereo)、深度相机(RGB-D)
深度相机能够读取每个像素离相机的距离
单目相机 只使用一个摄像头进行SLAM的做法叫做单目SLAM(Monocular SLAM),结构简单,成本低。
照片拍照的本质,就是在相机平面的一个投影,在这个过程当中丢失了这个场景的一个维度,就是深度(距离信息)

单目SLAM 估计的轨迹和地图,与真实的轨迹和地图之间相差一个因子,这就是所谓的尺度(scale)由于,单目SLAM无法凭借图像来确定真实的尺度,又称为尺度不确定
单目SLAM 的缺点:1、只有平移后才能计算深度 2、无法确定真实的尺度。
双目相机:

双目相机和深度相机的目的是,通过某种手段测量物体离我们之间的距离。如果知道这个距离,场景的三维结构就可以通过这个单个图像恢复出来,消除了尺度不确定性。
双目相机是由于两个单目相机组成,这两个相机之间的距离叫做基线(baseline)这个基线的值是已知的,我们通过这个基线的来估计每个像素的空间位置(就像是人通过左右眼的图像的差异,来判断物体的远近)
但是计算机双目相机需要大量的计算才能估计出每个像素点的深度。双目相机的测量到的深度范围与基线相关,基线的距离越大,能够检测到的距离就越远。双目的相机的缺点是:配置和标定都比较复杂,其深度测量和精度受到双目的基线和分辨率的限制,而且视差的计算非常消耗计算机的资源。因此在现有的条件下,计算量大是双目相机的主要问题之一。
深度相机是2010年左右开始兴起的一种相机,他的最大的特点就是采用红外结构光或者(Time-of-Flight)ToF原理,像激光传感器那样,主动向物体发射光并且接受返回的光,测量出物体离相机的距离。这部分并不像双目那样通过计算机计算来解决,而是通过物理测量的手段,可以节省大量的计算量。目前RGBD相机主要包括KinectV1/V2, Xtion live pro,Realsense,目前大多数的RGBD相机还存在测量范围小,噪声大,视野小,易受到日光干扰,无法测量透射材质等诸多问题。
经典视觉SLAM框架
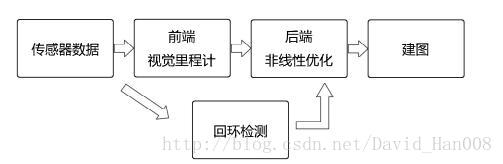
视觉slam的路程分成以下几步:
1、传感器信息的读取。
2、视觉里程计(Visual Odometry,VO)视觉里程计的任务是,估算相邻图像之间相机的运动,以及局部地图。VO也称为前端(Front End).
3、后端优化(Optimization)后端是接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息。(Back End)
4、回环检测(loop Closing)。回环检测是判断机器人是否或者曾经到达过先前的位置。如果检测到回环,它会吧信息提供给后端进行处理
5、建图(Mapping),他根据估计出的轨迹,建立与任务要求的对应的地图。
视觉里程计
视觉里程计关心的是,相邻图像之间相机的移动,最简单的情况就是计算两张图像之间的运动关系。
为了定量的估计相机的运动,必须了解相机与空间点的几何关系。
如果仅仅用视觉里程计来轨迹轨迹,将不可避免的出现累计漂移,注意,这个地方说的是累计漂移,
 ,
,
为了解决漂移问题。我们还需要两种检测技术:后端优化和回环检测的。回环检测负责吧“”机器人回到原来的位置“”这件事情给检测出来。而后端优化则是根据这个信息,优化整个轨迹形状
后端优化
后端优化主要是指在处理SLAM噪声问题,虽然我希望所有的数据都是准确的,但是在现实当中,再精确的传感器也是有一定噪声的。后端只要的考虑的问题,就是如何从带有噪声的数据中,估计出整个系统的状态,以及这个状态估计的不确定性有多大(最大后验概率(MAP))
视觉里程计(前端)给后端提供待优化的数据。
后端负责整体的优化过程,后端面对的只有数据,并不关系数据到底是来自哪个传感器。
在视觉SLAM当中,前端和计算机视觉领域更为相关,例如:图像的特征提取与匹配。后端只要是滤波和非线性优化算法。
回环检测
回环检测(闭环检测(Loop Closure Detection))主要是解决位置估计随时间漂移的问题。为了实现回环检测,我们需要让机器人具有识别曾经到达过场景的能力。通过判断图像之间的相似性,来完成回环检测。如果回环检测成功,可以显著地减小累计误差。所以视觉回环检测,实际上是一种计算图像数据相似性的算法。
建图
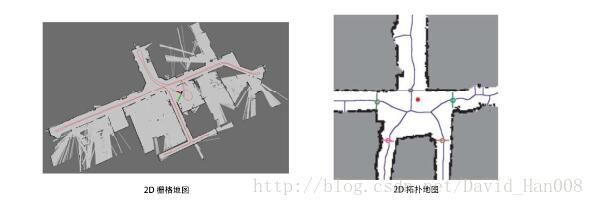
建图(Mapping)是指构建地图的过程。地图是对环境的描述,但是这个描述并不是固定。(如果是激光雷达的地图,就是一个二维的地图,如果是其他视觉slam 三维的点云图)
地图可以分成度量地图和拓扑地图两种。
1、度量地图(Metric Map)
度量地图强调的是精确表示出地图中物体的位置关系,通常我们用稀疏(Sparse)与稠密(Dense)对他们进行分类。稀疏地图进行了一定程度的抽象,并不需要表达所有物体。例如:我们需要一部分有代表意义的东西(简称为路标landmark),
这里的稀疏地图,就是又路标组成的地图。
相对于稀疏地图而言,稠密地图将建模所看到的所有的东西

对于定位而言:稀疏的路标地图就足够了。而要用于导航,我们往往需要稠密地图。
稠密地图通常按照分辨率,由许多个小块组成。二维的度量地图是许多小格子(Grid),三维则是许多小方块(Voxel)。一般而言,一个小方块,有占据,空闲,未知三种状态,来表达这个格子内是不是有物体。
一些用于视觉导航的算法 A*, D*,算法这种算法需要地图能够存储每个格点的状态,浪费了大量的存储空间。而且大多数情况下,地图的很多细节是无用的。另外,大规模度量地图有的时候回出现一致性问题。很小的一点转向误差,可能会导致两间屋子之间的墙出现重叠,使得地图失效。
2、拓扑地图(Topological Map)
相比于度量地图的精准性,拓扑地图则更强调了地图元素之间的关系。拓扑地图是一个图。这个图是由节点和边组成,只考虑节点间的连通性。它放松了地图对精确位置的需要,去掉了地图的细节问题,是一种更为紧凑的表达方式。
如何在拓扑图中,进行分割形成结点和边,如何使用拓扑地图进行导航和路径规划。
slam 的数学表述
通常机器人会携带一个测量自身运动的传感器,比如说码盘,或者惯性传感器。运动方程可以表示为:


与运动方程相互对应的观测方程。

假设机器人在平面中运动,他的位姿由两个位置和一个转角来描述,也就是![]()
同时如果运动传感器能够检测到机器人每两个时间间隔位置和转角的变换量![]() 那么此刻的运动方程就可以具体化:
那么此刻的运动方程就可以具体化:

这是比较理想的状态下。现实是,并不是所有的传感器都可以直接测量出位置和角度的变化。
假如机器人携带的是一个二维的激光雷达。我们知道激光传感器观测一个2D路标是时候,能够测量到两个量,一个是路标边到机器人之间的距离r 另一个是夹角![]() ,那么我们写出的观测方程就是:
,那么我们写出的观测方程就是:

在考虑视觉SLAM时候,观测方程就是“对路标点拍摄后,得到了图像中的像素”的过程。
针对不同的传感器,这两个方程有不同的参数化。如果我们保持通用性,吧他们们抽象成通用的抽象形式,那么SLAM过程可总结为两个基本过程:

将SLAM问题建模成一个状态估计问题。状态估计问题的求解,与这个两个方程的具体的形式有关,以及噪声服从那种分布有关。我们按照运动和观测方程是否为线性,噪声是否服从高斯分布,分成线性/非线性和高斯/非高斯系统。其中线性高斯系统(Line Gaussian,LG系统)是最简单的,他的无偏的最优估计可以由卡尔曼滤波器给出。而在非线性,非高斯的系统中,我们会使用扩展卡尔曼滤波器(EKF)和非线性优化两大类方法求解它。直到21世纪早期,以EKF为主,占据了SLAM的主导地位。到今天视觉SLAM主要都是以图优化来进行状态估计
机器人一般都是6自由度,三维空间的运动由三个轴以及绕这个三个轴的旋转量组成。一共有6个自由度。
CMakeLists.txt
#“#”表示注释
#声明要求cmake的最低的版本
cmake_minimum_required(VERSION 2.8)
#声明一个工程
project(HelloSlam)
#添加一个可执行文件
#语法
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 1
- 2
- 3
- 4
- 5
- 6
- 7
第三讲 三维空间的刚体运动



什么叫旋转向量:使用一个向量,他的方向和旋转轴一致,长度等于旋转角。(任意的一个旋转,都可以用旋转轴和旋转角来表示)这就是轴角Axis-Angle
Eigen::Matrix3d R = Eigen::AngleAxisd(M_PI/2, Eigen::Vector3d(0,0,1)).toRotationMatrix();
- 1
- 1
任意的旋转都可以使用角轴来描述,那么前面的这个参数表示的旋转的角度,后面的这个参数旋转向量
然后我们现在已知了旋转矩阵,通过![]() 公式求得特殊正交群。
公式求得特殊正交群。
在代码中是这样写的
Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从旋转矩阵构造 由旋转矩阵得到的
- 1
- 1
当然还有以下几种写法
Sophus::SO3 SO3_R(R); // Sophus::SO(3)可以直接从旋转矩阵构造 由旋转矩阵得到的
Sophus::SO3 SO3_v( 0, 0, M_PI/2 ); // 亦可从旋转向量构造
Eigen::Quaterniond q(R); // 或者四元数 这里是将R变成一个四元数
Sophus::SO3 SO3_q( q );
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
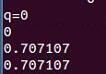
如何输出一个四元数
cout<<"q="<.coeffs()<;
- 1
- 1
这里coeffs输出的顺序是(x,y,z,w)前面的x,y,z为虚部 w是实部
Eigen::Vector3d t(1,0,0); // 沿X轴平移1
Sophus::SE3 SE3_Rt(R, t); // 从R,t构造SE(3)
Sophus::SE3 SE3_qt(q,t); // 从q,t构造SE(3)
cout<<"SE3 from R,t= "<<endl<<SE3_Rt<<endl;
cout<<"SE3 from q,t= "<<endl<<SE3_qt<<endl;
cout<<"se3 hat = "<<endl<<Sophus::SE3::hat(se3)<<endl;
cout<<"se3 hat vee = "<<Sophus::SE3::vee( Sophus::SE3::hat(se3) ).transpose()<<endl;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 1
- 2
- 3
- 4
- 5
- 6
- 7
一个刚体在三维空间中的运动是如何描述的。
平移是比较好描述的,旋转这件事比较困难。如何来描述旋转,我们使用:旋转矩阵、四元数、欧拉角
刚体:有位置信息,还需要有自身的姿态(姿态:就是相机的朝向)
结合起来:相机为与空间上(0,0,0)处,面朝正前方
这是关于坐标系,我们通过坐标系来描述一个向量。

外积就是将外积表达式拆开成为第2个式子,然后再a拆开,b表示列向量就变成a^b
a^表示把a这个向量变成一个矩阵,这个矩阵是a的反对称矩阵,
反对称矩阵就是 矩阵a的转置等于-a
这里a与b的外积是一个行列式,
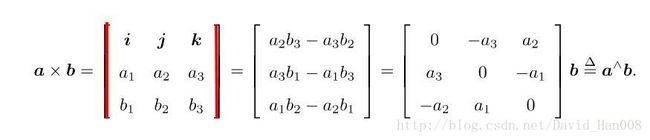
外积的物理意义是a和b组成的平行四边形的的面积
现在存在一个问题,同一个向量在不同的坐标系里面坐标该怎么表示?
在机器人运动过程中,我们设定的是惯性坐标系(世界坐标系),可以认为它是固定不动的
ZW,XW,YW是世界坐标系,ZC,XC,YC是相机的坐标系,P在相机坐标系中的坐标是PC,在世界坐标系中的坐标是PW,首先我们得到在相机坐标系中的 pc 然后通过变换矩阵T 来变换到PW
正交矩阵就是逆等于转置
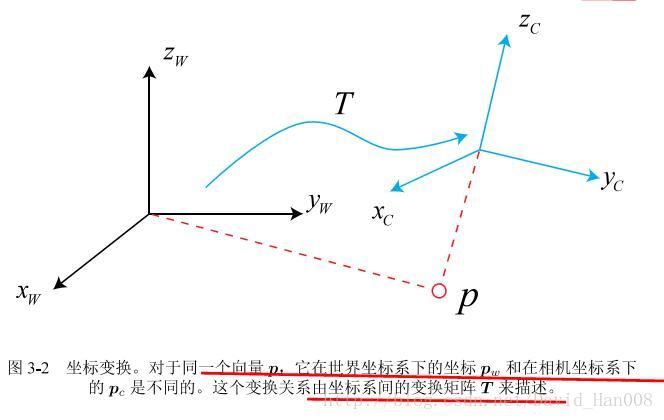
什么叫欧式变换?就是说同一个向量,在各个坐标系下的长度和夹角都不会发生改变。
欧式变换由一个旋转和一个平移两个部分组成(前提是刚体)
可以用旋转矩阵,来描述相机的旋转,旋转矩阵是一个行列式为1的正交矩阵。我们可以吧所有的旋转矩阵的集合定义如下:
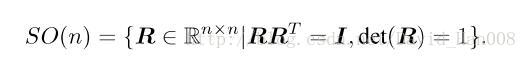
SO(n)是特殊正交群,这个集合由n维空间旋转矩阵组成,其中SO(3)就是三维空间的旋转,根据正交矩阵的性质,正交矩阵的逆和转置是一样的。
因此欧式空间的坐标变换可以写成:(一次旋转+一次平移)
![]()
但是这个表达式是非线性的,因此我们需要重写
1、引入齐次坐标(也是用4个数来表达三维向量的做法)

在三维向量的末尾添加1,成为4维向量,称为齐次坐标
这里要区分特殊欧式群和特殊正交群

实践部分,添加eigen的库
#include_directories("/usr/include/eigen3")
- 1
- 1
不需要加入target_link
声明部分
Eigen只需要关心前面3个参数,分别是:数据类型,行,列
声明一个2行3列的float类型的矩阵
Eigen::Matrix<float,2,3>matrix_23;
声明一个3行1列的向量 这里的d表示double
Eigen::Vector3d v_3d;
声明一个double类型的3*3的矩阵,并且初始化为零
Eigen::Matrix3d matrix_33=Eigen::Matrix3d::zero();
当不确定矩阵的大小的时候,可以申请动态矩阵
Eigen::Matrix<double,Eigen::Dynamic,Eigen::Dynamix> matrix_dynamc;
同样,可以表示为:
Eigen::MatrixXd matrix_x;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
赋值部分
为矩阵赋值
matrix_23<<1,2,3,4,5,6;
- 1
- 2
- 3
- 1
- 2
- 3
访问矩阵内部存储的数值
for(int i=0;i<2;i++){
for(int j=0;j<3,j++){
cout<"\t";
}
cout<
- 1
- 2
- 3
- 4
- 5
- 6
- 1
- 2
- 3
- 4
- 5
- 6
矩阵的四则运算
v_3d<<3,2,1;
vd_3d<<4,5,6;
矩阵的类型是一样
Eigen::Matrix<double,2,1>result=matrix_23.cast<double>()*v_3d;//输入想要改变矩阵的类型
在一个矩阵的后面 .cast<double>() 将原来的float转化的double类型
Eigen::Matrix<float,2,1>result2=matrix_23*vd_3d;//默认条件下矩阵的类型
- 1
- 2
- 3
- 4
- 5
- 6
- 1
- 2
- 3
- 4
- 5
- 6
矩阵的性质
产生随机数矩阵
matrix_33=Eigen::Matrix3d::Random();
求这个矩阵的转置
cout<cout<cout<cout<10<cout<cout< eigen_solver(matrix_33);
cout<cout<double, MATRIX_SIZE, MATRIX_SIZE > matrix_NN;
matrix_NN = Eigen::MatrixXd::Random( MATRIX_SIZE, MATRIX_SIZE );
Eigen::Matrix< double, MATRIX_SIZE, 1> v_Nd;
v_Nd = Eigen::MatrixXd::Random( MATRIX_SIZE,1 );
clock_t time_stt=clock();//用来计时
第一种方法:直接求逆
Eigen::Matrix<double,MATRIX_SIZE,1> x = matrix_NN.inverse()*v_Nd;
然后输出计算的时间
cout <<"time use in normal invers is " << 1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC << "ms"<< endl;
第二种方法:使用QR分解来求解
time_stt = clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout <<"time use in Qr compsition is " <<1000* (clock() - time_stt)/(double)CLOCKS_PER_SEC <<"ms" << endl;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
当矩阵的规模庞大的时候,使用QR分解更加高效
QR分解也叫做正交三角分解,把矩阵分解成一个正交矩阵与一个上三角矩阵的积。通常用来求解线性最小二乘法的问题
QR求解的方法:
- Givens变换求矩阵的QR分解
- Householder变换又称为反射变换或者镜像变换
- Gram-Schmidt正交化
由于旋转矩阵是用9个量来描述旋转的,并且有正交性约束和行列式值约束
我们希望能够一种更加紧凑的方式来系统的描述旋转和平移
因此,我们换了一种方式进行比较,就是需旋转轴和旋转角因此我们使用一个向量,这个向量的方向和旋转轴一致,长度等于旋转角,这种向量,称为旋转向量(或者轴角,Axis-Angle),也可以叫做角轴, 这种方法的优势在于,只需要一个三维的向量,就可以描述旋转。
作为一个承上启下的部分,旋转向量和旋转矩阵是如何转化呢?假设有一个旋转轴为n,角度为A,那么他对应的旋转向量是An,由轴角到旋转矩阵的过程由于罗德里格斯公式表明:

因此 旋转矩阵到轴角的表示方法:


欧拉角
优势:直观
欧拉角使用的三个分离的转角,把一次旋转分解成三次绕不同的轴的旋转
其中较为常用的ZYX轴旋转
欧拉角会出现奇异值(万向锁问题)
- 物体绕Z轴旋转之后得到偏航角yaw
- 绕Y轴之后得到俯仰角pitch
- 绕X轴旋转之后得到滚动角roll
因此我们可以使用[r,p,y]来表示任意的旋转 rpy角的旋转顺序是ZYX
RPY的参考链接:
http://blog.csdn.net/heroacool/article/details/70568858
缺陷:这种方法会碰到万向锁的问题,在俯仰角pitch为+- 90度的时候,第一次旋转和第三次旋转使用的同一个轴,使得系统丢失一个自由度。也成为万向锁
由于这个问题,欧拉角不适合用于插值和迭代,往往只是用于人机交互中,同样也不会在滤波和优化中使用欧拉角来表达旋转(因为具有奇异性)
四元数
旋转矩阵用9个量,来描述3自由度的旋转,具有冗余性,而欧拉角和旋转向量具有奇异性
在工程当中使用的四元数来存储机器人轨迹和旋转
例如,当我们想要用二维的量来表示地球表面的时候,必然会出现奇异性,例如,经纬度在+-90度的地方,毫无意义,因此想要表示三维的刚体的时候,我们就打算用四元数。四元数的优势在于1、紧凑,2、没有奇异性
一个四元数拥有一个实部和3个虚部 本质上是一种扩展复数,描述3维的量,用四元数



如何用四元数来表示三维刚体的旋转
假设,某个旋转是绕单位向量

结论在四元数中,任意旋转都可以有两个互为相反数的四元数来表示。
四元数到旋转矩阵的变换方式

反之,由旋转矩阵到四元数的变换如下:假设矩阵R={mij},其对应的四元数是:

相似、仿射、射影变换
这三种变换都会改变原来物体的外形
相似变换比欧式变换对了一个自由度,它允许物体进行均匀的缩放,其矩阵表示为:
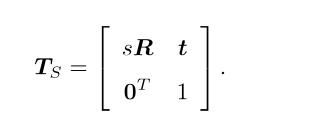
其中旋转矩阵部分多了一个缩放因子s,可以将x,y,z在三个坐标轴上面进行缩放
仿射变换
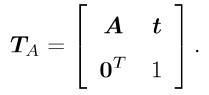
A只是要求是一个可逆矩阵,不要求是正交矩阵,仿射变换后的立方体就不再是方的买单时各个面仍然是平行四边形。
射影变换
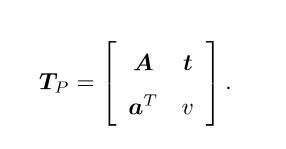
这是一个最一般的形式,一个正方形经过射影变换,最后变成一个规则的四边形
总结:

从真实世界到相机照片变换的过程就是一个射影变换。如果相机的焦距为无穷远的时候,那么这个变换是仿射变换。
实践部分:Eigen的几何模块
首先添加头文件#include<Eigen/Geometry>
Eigen/Geometry提供了各种旋转和平移的表示
声明一个3维的旋转矩阵
Eigen::Matrix3d rotation_matrix=Eigen::Matrix3d::Identity();
声明旋转向量,并且沿Z轴旋转45度
Eigen::AngleAxisd rotation_vecotr (M PI/4,Eigen::Vector3d(0,0,1));
cout .precision(3);//输出返回3位有效数字
cout<<rotation_vector.matrix()<<endl;
将旋转向量赋值给另外一个向量
rotation_matrix=rotation_vector.toRotationMatrix();
通过跟一个向量相乘从而进行坐标变换
Eigen::Vector3d v(1,0,0);
Eigen::Vector3d v_rotated=rotation_vector *v;
cout<<v_rotated.transport()<<endl;//将(0,0,1)旋转之后的向量转置输出
将一个向量(1,0,0)使用旋转矩阵之后的输出
v_rotated=rotation_matrix*v;//其实说白了,就是让这个旋转矩阵和这个向量相乘,然后重视[3*3]*[3*1]最后输出的结果就是3*1
cout<<v_rotated.transport()<<endl;//将(0,0,1)旋转之后的向量转置输出
可以将旋转矩阵直接转化成欧拉角,其实欧拉角存在的意义,只是为了方便人们理解,在程序当中,我们处理问题一般是用的四元数
Eigen::Vector3d euler_angles=rotation_matrix.eulerAngles(2,1,0);//这是输出的默认的数据是roll pitch yaw
如果逆向输出的顺序是yaw pitch roll,那么
cout<<"yaw pitch roll"<<euler_angles.transport()<<endl;
欧式变换阵 使用Eigen::Isometry
说的是三维空间下的变换Isometry3d
Eigen::Isometry T=Eigen::Isometry3d::Identity();
T.rotate(rotation_vector);//按照rotation_vector的方式进行旋转
T.pretranslate(Eigen::Vector3d(1,3,4));//吧这个向量进行平移
cout<<T.matrix()<<endl;
几种坐标变换的方式:1、用变换矩阵进行坐标变换
Eigen::Vector3d v_transformed=T*v;
关于四元数
Eigen::Quaterniond q=Eigen::Quaterniond(rotation_vector);
cout<<q.coeffs()<<endl;//这里coeffs输出的顺序是(x,y,z,w)前面的x,y,z为虚部 w是实部
同样也可以把旋转矩阵赋给他
q=Eigen::Quateriond(rotation_matrix)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
visualize_Geometry
#include
- 1
- 1
这个头文件对cin和cout这种操作符进行控制,例如可以控制输出位数,左对齐,右对齐等。
#include
- 1
- 1
pangolin是SLAM可视化的openGL的库
第四讲 李群李代数
由于相机的位姿是未知的,我们需要解决什么样的相机位姿最符合当前关键数据这样的问题
通过李群李代数之间的转换关系,我们希望把位姿估计变成无约束的优化问题。
特殊正交群SO(3),是由三维旋转矩阵构成的;特殊欧式群SE(3)是变换矩阵构成的
特殊正交群SO(3)就是,3*3的矩阵,然后正交,行列式为1,其定义是:
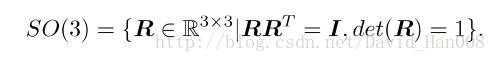
特殊欧式群SE(3),是在这个3*3矩阵基础上,转化成一个齐次的矩阵,为了避免非齐次带来的不便,其定义如下
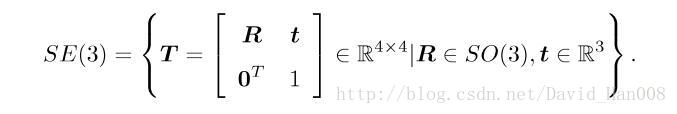
加法的封闭性a属于集合A,b也属于集合A,如果a+b也是属于集合A的话,这就叫做加法的封闭性
但是旋转矩阵和变换矩阵是没有加法封闭性的,但是他们的乘法是封闭的,也就是说

两个旋转矩阵相乘表示做了两次旋转。对于这种只有一个运算的集合,我们把他叫做群。
群
群是一种集合加上一种集合运算的代数结构,我们把集合记作A,运算符号记作 · ,那么一个群可以记作 G=(A, ·),群这种运算要求满足以下几个条件:
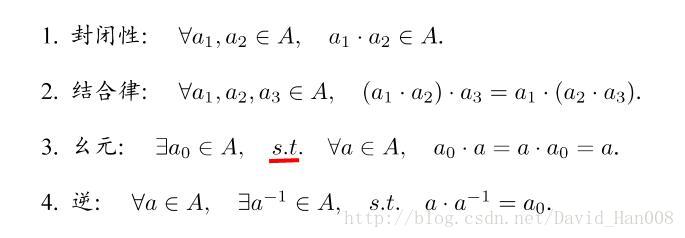
s.t.表示约束条件
总结:旋转矩阵和矩阵的乘法运算构成旋转矩阵群;变换矩阵和矩阵乘法构成变换矩阵群
李群 Lie Group
李群,是指的具有连续(光滑)性质的群,SO(n),SE(n)是李群。因为每个李群都有对应的李代数因此,我们先引出李代数so(n)
李代数的引出
我们每次想要求一个旋转矩阵的导数,就可以左乘一个矩阵![]() 即可,
即可,
我们根据导数的定义,在R(t)的0附近进行一阶泰勒展开式
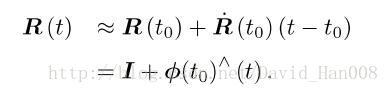
他是推到了,如果一个导数等于他本身,那么这个导数就是e^x这个函数,即:

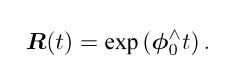
每个李群都对应一种李代数
由于每个李群都有李代数,李代数描述了李群的局部性质。
李代数由一个集合V,一个数域F,和一个二以下元运算[,]组成,如果他们满足以下几条性质,称(V,F,[,])为一个李代数,记作 g
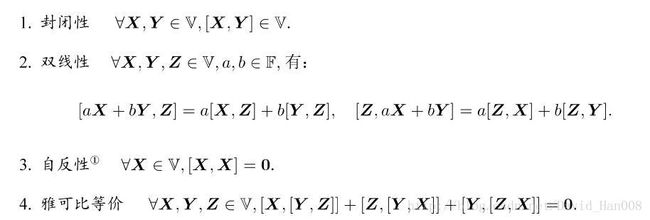
[ ]这个运算符叫做李括号,要求元素和自己做李括号这种运算之后为0,也即是[x,x]=0,李括号直观上来讲是表达了两个元素之间的差异
李代数so(3)
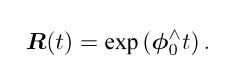 在这个式子总的
在这个式子总的![]() 就是SO(3)对应的李代数,记作so(3)
就是SO(3)对应的李代数,记作so(3)
so(3)是一个三维的向量组成的集合,每个向量都对应着一个反对称的矩阵,来表达旋转矩阵的导数
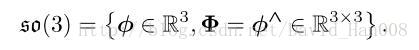
SO(3)和so(3)之间的映射关系是:
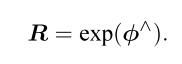
同理:SE(3)也是有对应的李代数的se(3)
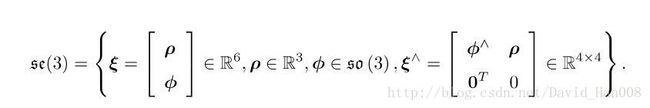
他是一个6维的向量,前三维表示平移,记作![]() ,后面三维表示旋转,记作:
,后面三维表示旋转,记作:![]() ,
,
![]()
SO(3)上的指数映射的物理意义就是旋转向量
为什么我们要有李代数,因为我们需要解决李群上面只有乘法没有加法这个问题。
利用BCH线性近似,来推导so(3)和se(3)上的导数和扰动波形,通常情况下,扰动模型比较简洁,更加常用。
实践部分:使用sophus库
编译部分:到高博的3rdparty,然后解压sophus,然后mkdir build cd build cmake .. make 就可以了。
cmake .. 编译的时候出现这幅图是正常的。当还以为有问题呢?看来是多虑的

视觉SLAM第5讲

opencv各个版本的github上的链接:
https://github.com/opencv/opencv/releases
安装opencv3.1.0遇到的问题:
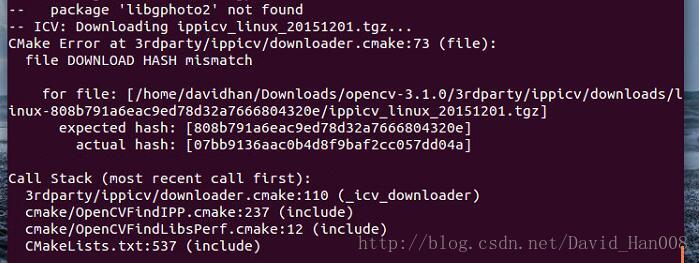
找到的解决方案:
http://blog.csdn.net/huangkangying/article/details/53406370
然后
// 关于 cv::Mat 的拷贝
// 直接赋值并不会拷贝数据
cv::Mat image_another = image;
// 修改 image_another 会导致 image 发生变化
image_another ( cv::Rect ( 0,0,100,100 ) ).setTo ( 0 ); // 将左上角100*100的块置零
cv::imshow ( "image", image );
cv::waitKey ( 0 );
// 使用clone函数来拷贝数据
cv::Mat image_clone = image.clone();
image_clone ( cv::Rect ( 0,0,100,100 ) ).setTo ( 255 );
cv::imshow ( "image", image );
cv::imshow ( "image_clone", image_clone );
cv::waitKey ( 0 );
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
第一种方式,拷贝数据的话是浅拷贝,就是说,你如果该数据,那么原始的数据也会改变。
第二种方式,在拷贝数据的时候用image.clone()那么这样不会修改原始的数据。
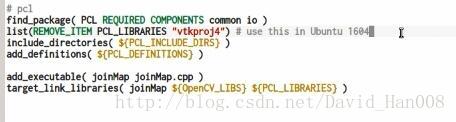
Ubuntu16.04须知:
安装pcl
sudo apt-get install libpcl-dev pcl-tools
- 1
- 1
并且在使用的时候,cmakelist需要这么写:
joinMap.cpp
用来读写文件的
#include
- 1
- 1
将图像都放到一个容器当中,<这里面试数据类型>
vector
- 1
- 2
- 1
- 2
利用fin来读取txt当中的参数
ifstream fin("./pose.txt");//导入相机的位置和姿态的数据
- 1
- 1
为了使用boost::format
#include
- 1
- 1
boost::format格式化字符串
boost::format fmt( "./%s/%d.%s" ); //图像文件格式
- 1
- 1
容器的基本使用:http://blog.csdn.net/ws_20100/article/details/50829327
这里.push_back是在这个容器的尾部插入、push_back(图片)
colorImgs.push_back( cv::imread( (fmt%"color"%(i+1)%"png").str() ));
depthImgs.push_back( cv::imread( (fmt%"depth"%(i+1)%"pgm").str(), -1 )); // 使用-1读取原始图像
- 1
- 2
- 1
- 2
这里用来遍历data的
double data[7] = {0};//初始化
for ( auto& d:data )
fin>>d;
- 1
- 2
- 3
- 1
- 2
- 3
参考链接:c++11 for http://blog.csdn.net/hackmind/article/details/24271949
将图像的外参
for ( int i=0; i<5; i++ )
{
boost::format fmt( "./%s/%d.%s" ); //图像文件格式
colorImgs.push_back( cv::imread( (fmt%"color"%(i+1)%"png").str() ));
depthImgs.push_back( cv::imread( (fmt%"depth"%(i+1)%"pgm").str(), -1 )); // 使用-1读取原始图像
//将相机的外参数,都给了T
double data[7] = {0};
for ( auto& d:data )
fin>>d;//将上面的每个图片的外参都给了d
Eigen::Quaterniond q( data[6], data[3], data[4], data[5] );
Eigen::Isometry3d T(q);//定义一个欧式变换矩阵,
T.pretranslate( Eigen::Vector3d( data[0], data[1], data[2] ));
poses.push_back( T );//将这里的数据,添加的相机的位子当中,进行重新的排序
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
在点云拼接部分:
opencv当中颜色通道是bgr的顺序
cv::Mat color = colorImgs[i];
cv::Mat depth = depthImgs[i];
Eigen::Isometry3d T = poses[i];
for ( int v=0; v<color.rows; v++ )
for ( int u=0; u<color.cols; u++ )
{
unsigned int d = depth.ptr ( v )[u]; // 深度值
if ( d==0 ) continue; // 为0表示没有测量到
Eigen::Vector3d point; //声明一个3维的列向量
point[2] = double(d)/depthScale;
point[0] = (u-cx)*point[2]/fx;
point[1] = (v-cy)*point[2]/fy;
Eigen::Vector3d pointWorld = T*point;
//XYZRGB,在opencv当中,
PointT p ;
p.x = pointWorld[0];
p.y = -pointWorld[1];
p.z = pointWorld[2];
p.b = color.data[ v*color.step+u*color.channels() ];
p.g = color.data[ v*color.step+u*color.channels()+1 ];
p.r = color.data[ v*color.step+u*color.channels()+2 ];
pointCloud->points.push_back( p );
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
opencv当中的 .step参数表示的实际像素的宽度 .channel()表示的是,通道的提取
关于图像上下翻转问题,是因为opencv定义的坐标系和pcl_viewer显示坐标系不同,opencv是x右y下,而pcl显示是x右y上。解决方法:找到群主程序函数中,把计算点空间坐标的公式的p.y值添加负号,这样y方向就可以正常显示了,so easy。(或许还有别的方法)

最后保存文件
cout<<"点云共有"<<pointCloud->size()<<"个点."<<endl;
pcl::io::savePCDFileBinary("map.pcd", *pointCloud );
- 1
- 2
- 1
- 2
视觉SLAM和激光SLAM的区别在于,观测模型不同。(他们的运动模型是相同的)
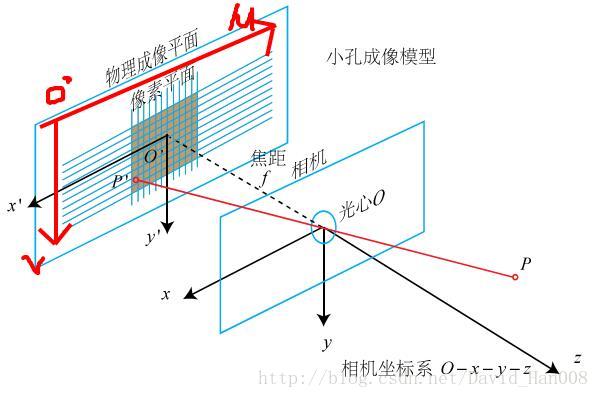
观测模型当中最常用的就是针孔相机模型
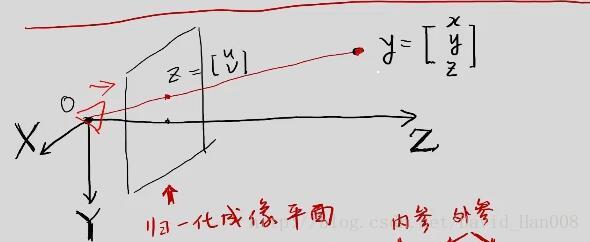
相机能够将三维世界中的坐标点(单位米)映射到二维图像平面(单位像素)的过程用一个几何模型进行讨论。
针孔相机模型
针孔相机模型,就是利用了相似三角形的知识

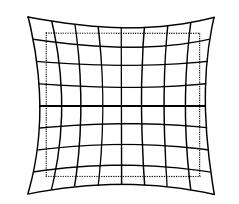
径向畸变由透镜形状引起的畸变,就是径向畸变
主要分成两大类:桶性畸变和枕形畸变
桶形畸变是由于图像放大率随着离光轴的距离的增加而减小
枕形畸变是图像的放大率随着光轴距离的增加而增加
切向畸变:相机在组装的过程中由于 透镜和成像平面不是严格平行的 导致的切向畸变
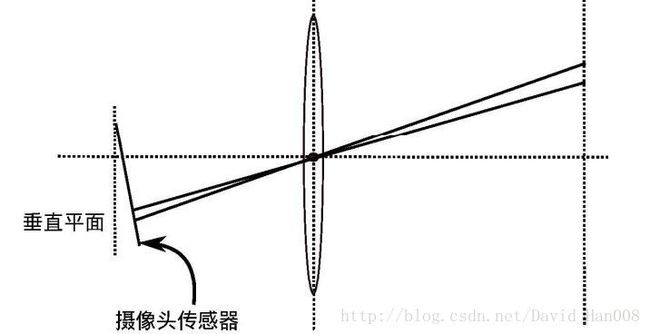
像素坐标系的定义:
像素坐标系与成像平面之间的差别:
相差了一个缩放和原点的平移

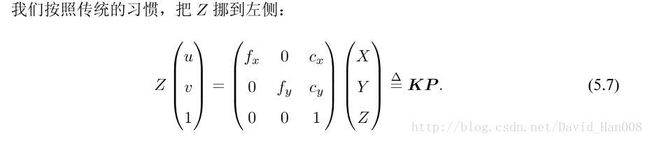
通常我们把中间的量组成的矩阵称为相机的内参数矩阵K。通常认为相机在内参在出厂之后是固定不变的,有的却没有,这个时候就是需要标定一下,但是我觉得标定这件事
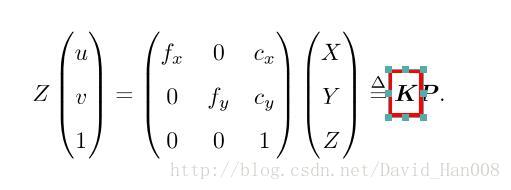

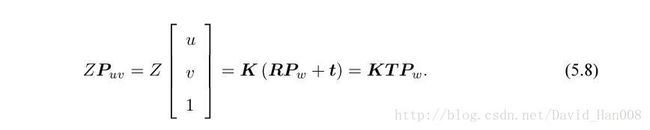

畸变
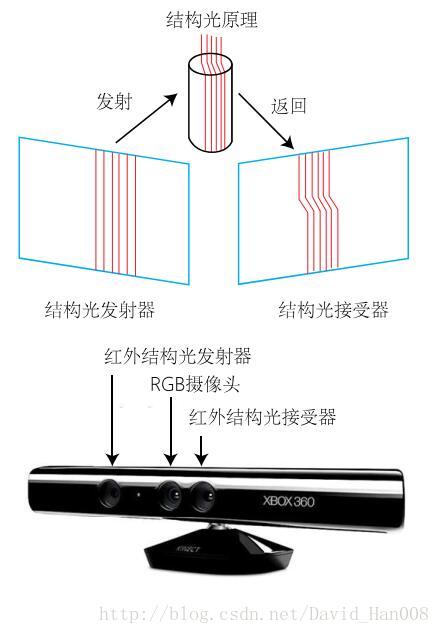
RGB-D相机模型
目前的RGB-D相机按照原理可以分成两类
1、通过红外光结构(structured light)来测量像素的距离,例如:Kinect1 Project Tango1、Intel Realsense
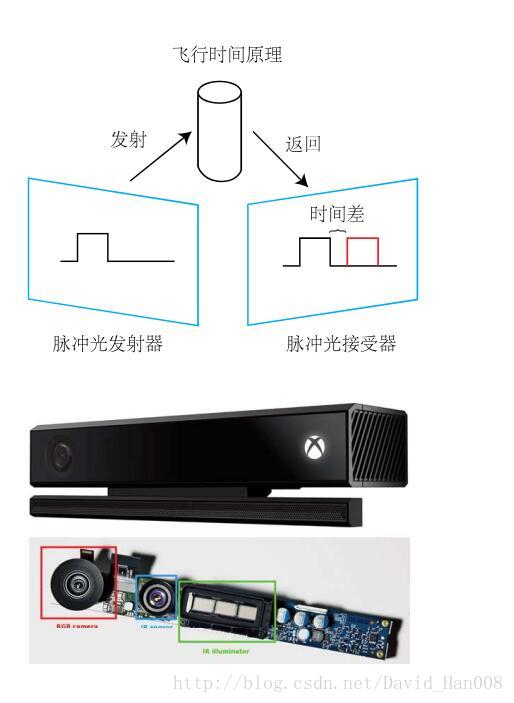
2、通过飞行时间法(Time-of-light,ToF)原理来测量像素的的距离。例如有KInect2和一些Tof传感器
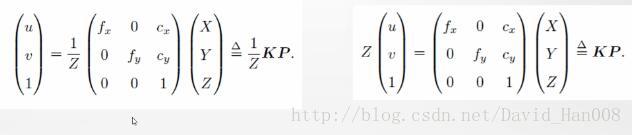
标定K就是相机的内参
视觉SLAM第6讲状态估计的问题
总结




安装g2o使用的是高博的slambook中的g2o
安装了依赖项之后编译好顺利啊
sudo apt-get install libeigen3-dev libsuitesparse-dev libqt4-dev qt4-qmake
然后cd 进g2o
mkdir build
cd build
cmake ..
make -j8
sudo make install
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 1
- 2
- 3
- 4
- 5
- 6
- 7
安装cerse
sudo apt-get install liblapack-dev libsuitesparse-dev libcxsparse3.1.2 libgflags-dev libgoogle-glog-dev libgtest-dev
然后cd 进cerse
mkdir build
cd build
cmake ..
make -j8
sudo make install
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 1
- 2
- 3
- 4
- 5
- 6
- 7
实践部分,我们已知带有噪声的x,y, 我们想要求得参数a,b,c
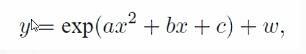
// 代价函数的计算模型
struct CURVE_FITTING_COST
{
CURVE_FITTING_COST ( double x, double y ) : _x ( x ), _y ( y ) {}
// 残差的计算 初始化
template <typename T>
bool operator() (
const T* const abc, // 模型参数,有3维
T* residual ) const // 残差
{
residual[0] = T ( _y ) - ceres::exp ( abc[0]*T ( _x ) *T ( _x ) + abc[1]*T ( _x ) + abc[2] ); // y-exp(ax^2+bx+c) 这就是误差
return true;
}
const double _x, _y; // x,y数据
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
ceres::Problem problem;
for ( int i=0; i// 向问题中添加误差项
// 使用自动求导,模板参数:误差类型,输出维度,输入维度,维数要与前面struct中一致
new ceres::AutoDiffCostFunction1, 3> (
new CURVE_FITTING_COST ( x_data[i], y_data[i] )
),
nullptr, // 核函数,这里不使用,为空
abc // 待估计参数
);
}
// 配置求解器
ceres::Solver::Options options; // 这里有很多配置项可以填
options.linear_solver_type = ceres::DENSE_QR; // 增量方程如何求解 指定QR分解
options.minimizer_progress_to_stdout = true; // 输出到cout
ceres::Solver::Summary summary; // 优化信息
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
ceres::Solve ( options, &problem, &summary ); // 开始优化
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_castdouble>>( t2-t1 );
cout<<"solve time cost = "<" seconds. "<// 输出结果
cout<cout<<"estimated a,b,c = ";
for ( auto a:abc ) cout<" ";
cout<return 0;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
输出结果
Ceres Solver Report: Iterations: 22, Initial cost: 1.824887e+04, Final cost: 5.096854e+01, Termination: CONVERGENCE
estimated a,b,c = 0.891943 2.17039 0.944142
- 1
- 2
- 1
- 2
迭代了22次,最开始的误差是Initial cost: 1.824887e+04
最后的误差是:inal cost: 5.096854e+01,最后收敛的原因是,Termination: CONVERGENCE,函数收敛了。
最后得出a,b,c的数值是estimated a,b,c = 0.891943 2.17039 0.944142
优化处理噪声数据
sfm : 就是从很多副图像中进行三维重建 struct of motion
想要跟高博一样,画出比价好看的图,写论文。
data=load('C:\Users\Administrator\Desktop\d0.txt');
x=data(:,1);
y=data(:,2);
scatter(x,y,10,'o')
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
scatter用于画散点图、
X和Y是数据向量,以X中数据为横坐标,以Y中数据位纵坐标描绘散点图,点的形状默认使用圈。、
scatter(x,y,10,’filled’)
scatter3(x,y,z)描述的三维图像
其实简单点:
plot(x,y,'o')
- 1
- 1
将点状图和曲线拟合图结合起来
data=load('C:\Users\Administrator\Desktop\d0.txt');
x=data(:,1);
y=data(:,2);
a=0.891943;
b=2.17039;
c=0.944142;
y1=exp(a*x.^2+b*x+c);%注意这里是点乘,相当于把矩阵中每个数字都平方。不能用* ,因为*表示的矩阵的乘法
figure(1)
plot(x,y,'o',x,y1)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
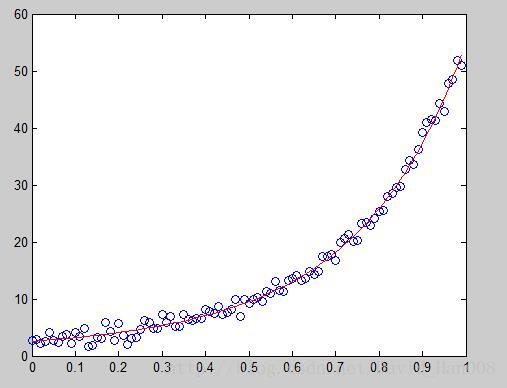
总结:其实有用的数据就是要求的a,b,c三个参数,然后我带迭代的次数,和如何迭代说明一下,就可以了
关于g2o求解同样的问题:
将优化问题用图的方式表示出来。一个图有若干个顶点(Vertex),以及连接这些节点的边(Edge),我们用顶点表示需要优化的变量,用边表示误差项。求最短路径,和无向图,就是找关于最短路径的边,是的求解问题最简单
g2o实现
// 构建图优化,先设定g2o
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; // 每个误差项优化变量维度为3,误差值维度为1
Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器
Block* solver_ptr = new Block( linearSolver ); // 矩阵块求解器
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
// 梯度下降方法,从GN, LM, DogLeg 中选
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );
// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );
// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm( solver ); // 设置求解器
optimizer.setVerbose( true ); // 打开调试输出
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 1
- 2
- 3
- 4
- 5
- 6
- 7
// 往图中增加顶点
CurveFittingVertex* v = new CurveFittingVertex();
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );
- 1
- 2
- 3
- 4
- 5
- 1
- 2
- 3
- 4
- 5
// 往图中增加边
for ( int i=0; inew CurveFittingEdge( x_data[i] );
edge->setId(i);
edge->setVertex( 0, v ); // 设置连接的顶点
edge->setMeasurement( y_data[i] ); // 观测数值
edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge( edge );
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
// 执行优化
cout<<"start optimization"<<endl;
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.initializeOptimization();
optimizer.optimize(100);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );
cout<<"solve time cost = "<<time_used.count()<<" seconds. "<<endl;
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
// 输出优化值
Eigen::Vector3d abc_estimate = v->estimate();
cout<<"estimated model: "<<abc_estimate.transpose()<<endl;
- 1
- 2
- 3
- 1
- 2
- 3
class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
virtual void setToOriginImpl() // 重置
{
_estimate << 0,0,0;
}
virtual void oplusImpl( const double* update ) // 更新
{
_estimate += Eigen::Vector3d(update);
}
// 存盘和读盘:留空
virtual bool read( istream& in ) {}
virtual bool write( ostream& out ) const {}
};
// 误差模型 模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差
void computeError()
{
const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
_error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;
}
virtual bool read( istream& in ) {}
virtual bool write( ostream& out ) const {}
public:
double _x; // x 值, y 值为 _measurement
};
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
视觉slam第7讲视觉里程计1
ICP是指,利用点云的匹配关系,来求解相机的三维运动。
PNP是利用已知的三维结构与图像的对应关系,来求解相机的三维运动。
对极几何,利用对极几何的约束,恢复出图像之间的相机的三维运动。
视觉里程计,分成特征提取和不提取特征,特征提取运行稳定,对光照,动态物体不敏感。
我们就是用图像的特征来代表这个图像。特征点在相机运动后保持稳定。图像的角点就是图像的特征。
角点的局限:例如:从远处上看上去是角点的地方,当相机走近后,可能就是角点了。或者,当旋转相机的时候,角点的外观会发生变换。
进而,我们提出了SIFT,SURF,ORB特征。
特征点:关键点(key-point)和描述子组成。
当我们谈论SIFT特征的时候,是指的提取SIFT关键点,并且计算SIFT描述子。关键点是指的特征点在图像中的位置,有些特征点具有朝向和大小的等信息。描述子通常是一个向量,这个向量是人为设计的,描述了该关键点周围像素的信息。
描述子是按照:外观相似的特征应该具有相似的描述子的原则设计的。
因此,只要两个特征点的描述子在向量空间上的距离相近,就可以认为他们是同样的特征点。
**FAST只有关键点,是没有描述子的。**ORB特征则是目前最具有代表性的实时图像特征,他改进了FAST检测子不具有方向性的问题。并且采用速度极快的二进制描述子BRIEF,使得整个图像的特征提取环节大大加速。
ORB特征也是采用的关键点和描述子两部分组成。*他的关键点是“Oriented FAST”是一种改进的FAST角点。他的描述子是BRIEF。*
FAST是一种角点,主要检测局部像素灰度变化明显的地方。他的思想是:如果一个像素与他的邻域内的像素差别较大,过亮或者过暗,那么他就是角点。FAST只需要比较像素的大小,因此十分快捷。
FAST角点提取:提取出FAST角点,计算了特征点的主方向。

FAST是一种角点,他的思路是:
1、在图像中选取像素p,假设他的亮度是IP
2、设置一个阈值T,例如T=IP*20%
3、以像素p为中心,选取半径为3的圆上的16个像素点, 这里的3应该是三个像素框
4、如果在选取的圆上面,有连续N个点的亮度值大于IP+T(1.2*IP))或者小于IP-T(0.8*IP),那么像素p通常可以被认为是特征点(N通常取12,FAST-12,通常n取9和11,的时候,称为FAST-9和FAST-11)
FAST-12算法中为了能够更加高效的提取特征点,添加一个预测试的技术,能够快速地排除大多数不是角点的元素,对于每个像素,直接检测在邻域圆上的第1,5,9,13个像素的亮度,只有当这四个像素当中有三个同时大于IP+T或者小于IP-T的时候,当前像素才有可能是是角点。FAST特征点的计算,仅仅是比较像素间亮度的差异,速度非常快,但是也存在一些问题:FAST特征点的数量很多,并且不是确定,而大多数情况下,我们希望能够固定特征点的数量。
在ORB当中,我们可以指定要提取的特征点数量。对原始的FAST角点分别计算Harris的响应值,然后选取前N个点具有最大相应值的角点,作为最终角点的集合。
FAST角点不具有方向信息,由于他取自半径为3的圆,存在尺度问题:从远处看是角点,但是近看却不是角点(就像是图像的金字塔)。因此ORB当中添加了尺度和旋转的描述。尺度不变性构建的图像的金字塔,并且从每一层上面来检测角点。旋转性是由灰度质心法实现。
质心是指以图像块灰度值作为权重的中心。(目标是为找找到方向)
1、在一个小的图像块B中,定义图像块的矩为:
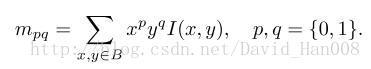
2、通过矩找到图像块的质心
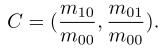
3、连接图像块的几何中心o与质心C,得到一个oc的向量,把这个向量的方向定义特征点的方向
![]()
**总结:**Oriented FAST的方向就是几何中心指向质心的方向
在尺度不变的问题上,采用图像金字塔,进行非极大值抑制。
BRIEF描述子
我们在提取到 Oriented FAST关键点后,我们需要对每个关键点计算其描述子。
BRIEF是二进制描述子,它的描述向量是由许多个0和1组成,这里的0和1编码了关键点附近的两个像素p和q的大小关系,如果P>Q,则取1 ;如果P
#include detector=ORB::create();
Ptr matcher=ORB::create();
//使用这个detect去检测两个图像,然后返回值是一个keyPoint类型的数组 提取角点的位置
detector->detect(img_1,keypoints_1);
detector->detect(img_2,keypoints_2);
//根据角点的位置,计算BRIEF描述子
descripiton->compute(img_1,keypoint_1,description_1);
description->compute(img_2,keypoint_2,description_2);
//然后使用huigui模块,将特征点画出来
Mat outimg1;
drawKeypoints(img_1,keypoints_1,outimg1,Scalar::all(-1),DrawMatchesFlags::DEFAULT);
imshow(outimg1);
//对两幅图片的BRIEF描述子进行匹配,使用hamming距离,返回的matches.
vectordouble dist=matches[i].distance;//获取当前点的距离,注意这里min的初始10000,max的初始值是0
if(distif(dist>max_dist) max_dist=dist;
}
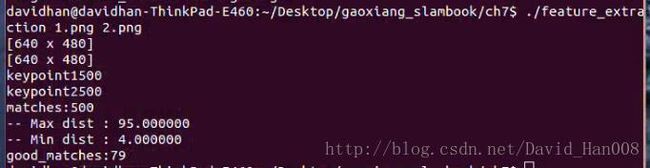
//高博的输出结果是:最近的两个量的匹配的距离是4,最远的匹配距离是95
//当描述子距离大于两倍的最小距离时,即认为有误匹配。这是工程经验
//但是最小距离会非常小,设置一个经验值30作为下限
//这里初始化汉明距离
Ptr matcher=DescriptiorMatcher::create("BruteForce-Hamming");
std::vectorif(matches[i].distance<=max(2*min_dist,30))
{
good_matches.push_back(matches[i]);
}
}
//最后将这些点都画出来
Mat img_goodmatch;
drawMatches(img_1,keypoint_1,img_2,keypoint_2,good_matches,img_goodmatch);
imshow("good_matches".img_goodmatch);
waitKey(0);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
我想想要查看在描述子不同额清下,经过某种手段对描述子进行筛选,
想要知道描述字的大小:
std::cout<.size()<<std::endl;
- 1
- 1
想要输出图片的信息
cout<.size()<;
- 1
- 1
附录:
ORB::creat() 资料参考链接:
http://blog.csdn.net/xizero00/article/details/43216727
智能指针只有三个:
auto_ptr unique_ptr shared_ptr
从上面的结果当中,我们可以发现,如果没有筛选匹配结果,那么提取的特征有大量的无匹配。因此,我们筛选的依据:汉明距离小于最小距离的两倍,并且大于30.(这是工程经验)
对描述子的构造传入的string类型
![]()
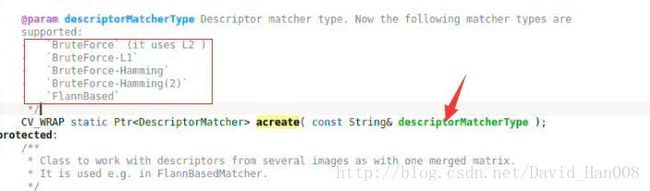
L1是1范数,就是绝对值的差
L2是2范数,也就是欧式距离
可以在这里修改成200个特征点 ORB默认的500个特征点
![]()

如果得到的是两个单目图像,得到就是2D-2D之间的对应关系 –使用对极几何
如果得到的是帧和地图,得到就是3D-2D之间的对应关系 –使用对极几何
如果得到的是RGBD图像,得到就是3D-3D之间的对应关系 –使用对极几何
总结:

注意:这里的s1和s2分别表示特征点1和特征点2的深度。
#include detector=ORB::create();
Ptrdescriptor=ORB::create();
Ptr matcher=Descriptor::create("BruteForce-Hamming");
detector->detect(img_1,keypoints_1);
detector->detect(img_2,keypoints_2);
descriptor->compute(img_1,keypoints_1,descriptors_1);
descriptor->compute(img_2,keypoints_2,descriptors_2);
vectorif(match[i].distance2*min_dist,30))
{
matches.push_back(match[i]);
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
//使用归一化坐标系
Point2d pixel2cam(const Point2d& p,const Mat& K);
{
return Point2d
(
(p.x-K.at<double>(0,2))/k.at<double>(0,0),
(p.y-K.at<double>(1,2))/k.at<double>(1,1))
)
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
void pose_estimation_2d2d(
std::vector的形式
vector//计算本质矩阵需要相机光心和相机的焦距
Point2d principal_point(325.1,249.7);//相机光心
double focal_length=521;//相机焦距
Mat essential_matrix;
essential_matrix=finEssentialMat(points1,points2,focal_length,principal_point);
cout<<"essential_matrix="<//单应矩阵,单应矩阵针对当是一个平面,需要针对初始化
Mat homography_matrix;
homography_matrix=findHomography(points1,points2,RANSAC,3);
cout<<"homography_matrix="<//从本质矩阵恢复旋转和平移
recoverPose(essential_matrix,points1,points2,R,t,focal_length,principal_point);
cout<cout<
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
points1.push_back(keypoints_1[matches[i].queryIdx].pt);
points2.push_back(keypoints_2[matches[i].trainIdx].pt);
- 1
- 2
- 1
- 2
在图像匹配的时候有两种图像的集合,查找集(Query set)和训练集(Train set)

总这份图片当中可以看出,是一个int类型。
funfamental_matrix=findFundamentalMat(points1,points2,CV_FM_8POINT)
- 1
- 1
int main(int argc,char **argv)
{
Mat img_1=imread(argv[1],CV_LOAD_IMAGE_COLOR);
Mat img_2=imread(argv[2],CV_LOAD_IMAGE_COLOR);
vector//估计相机运动
Mat R,t;
pose_estimation_2d2d(keypoints_1,keypoints_2,matches,R,t);
//验证:E=t^R*scale
Mat t_x=(Mat_<double>(3,3)<<
0, -t.at<double>(2,0),t.at<double>(1,0),
t.at<double>(2,0),0,-t.at<double>(0,0),
-t.at<double>(1,0),t.at<double>(0,0),0);
cout<<"t^R"<//验证对极约束
Mat K=(Mat_<double>(3,3)<<520.9,0,325.1,0,521.0,249.7,0,0,1);
for(DMatch m:matches)
{
Point2d pt1=pixel2cam(keypoints_1[m.queryIdx].pt,K);
Mat y1=(Mat<double>(3,1)<1);
Point2d pt2=pixel2cam(keypoints_2[m.trainIdx].pt,K);
Mat y2=(Mat<double>(3,1)<1);
Mat d=y2.t()*t_x*R*y1;
cout<<"epipolar constraint ="<return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
本质矩阵和基础矩阵之间的差别,基础矩阵多了一个相机的内参K。
由于尺度的不确定性。在程序中输出的t的第一维是是0.822,但是这个0.822的单位到底是0.822米,还是0.822厘米。我们是没有办法确定的。因为t乘以任意比例常数之后,对极约束仍然成立。
单目相机的初始化,不能只有纯旋转,必须要有一定程度的平移
多于8对点的情况下当给定的点数8对(例如上面这个例子当中找到了79对),我们可以计算一个最小二乘解。在存在误匹配的情况下,我们会更倾向于使用随机采样一致性(Random Sample Concensus,RANSAC)来求,而不是用最小二乘。RANSAC是一种通用的做法,适用于有很多误匹配的情况下。
三角测量(Triangulation)或者三角化
我们上一步当中,使用对极几何约束估计了相机的运动。下一步我们需要用相机的运动估计特征点的空间位置。在单目SLAM当中,由于我们无法通过单张图像获得相机的深度,因此我们通过三角测量的方法来估计地图点的深度。
三角测量是指:通过两处观察同一个点的夹角。来确定该点的距离。我们使用三角化来估计像素点距离。

因此我们可以通过最小二乘法来求解。
void triangulation(
std::vectorfloat>(3,0);
Point3d P(
x.at<float>(0,0),
x.at<float>(1,0),
x.at<float>(2,0)
);
points.push_back(p);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
//三角化
vector//第一张图片
Point2d pt1_cam=pixel2cam(keypoints_1[matches[i].queryIdx].pt,K);
Point2d pt1_cam_3d(
points[i].x/points[i].z,
points[i].y/points[i].z
);
cout<<"point in the first camera"<cout<<"point project from 3D"<//第二张图片
Point2f pt2_cam=pixel2cam(keypoints_2[mathces[i].trainIdx].pt,K);
Mat pt2_trans=R*(Mat_<double>(3,1)<double>(2,0);
cout<<"point in second camera"<cout<<"point reprojected from second frame"<
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
三角测量是由平移得到的,有平移才会有对极几何中的三角形。
在纯旋转的情况下无法使用三角测量。因为在纯旋转的情况下,对极约束永远满足。
当平移很小的时候,像素上的不确定性将导致较大的深度的不确定性。想要增加三角化的精度,其一就是提高特征点的提取精度,也就是提高图像的分辨率,另一种方法,是的平移量增大。总而言之,增大平移会使得匹配失效,而平移太小,则三角化的精度不够。
PnP(Perspective-n-Point)是求解3D到2D点对运动的方法。这种方法,描述了当我知道n个3D空间的点,以及它的投影位置的时候,如何来估计相机所在的位姿。
2D-2D的对极极化方法需要8个或者8个以上的点,且存在初始化,纯旋转和尺度的问题
在双目或者RGBD的视觉里程计中,特征点的位置,可以由三角化(双目),或者RGBD的深度图确定,那么我们可以直接进行pnp。而在单目相机中,必须进行初始化,才能进行pnp。
3D-2D的方法,不需要对极约束,同时可以在很少的匹配点中获得较好的运动估计,因此是一种十分重要的姿态估计的方法。
pnp问题又很多求解方法,例如 针对三对点的P3P ; 直接线性变换 DLT ; EPnP(Efficient);UPnP。此外还可以有非线性优化的方式构造最小二乘问题并迭代求解,也就是Bundle Adjustment.
DLT直接线性变换

p3p
仅仅使用三对匹配点,对数据要求较少
在SLAM问题中,通常都是先通过P3P等方法来估计相机的位姿,然后构建最小二乘问题进行Bundle Adjustment.
SVD奇异值分解
ICP求解。在唯一解的情况下,只要能找到极小值解,那么这个极小值就是全局最优值,这也就意味着ICP可以任意选定初始值 在RGBDslam当中,由于一个像素的深度数据可能是测不到。所有我们可以混合使用pnp和ICP。对于深度已知的特征点,对3D-3D建模误差。对于深度未知的特征点,建模3D-2D的重投影误差。
在实际方面,可以用eigen库直接求出。
扩展:参考冯兵的博客 实现一个简单的视觉里程计
视觉里程计的就是通过分析处理图像来确定机器人当前的位姿
输入:视频流+相机的内参
输出:每一帧相机的位姿
基本过程:
1、获取图像
2、对图像进行处理
3、通过FAST算法对图像进行特征检测,通过KLT跟踪图像的特征,如果跟踪的特征有所丢失,特征数小于某个阈值,那么重新特征检测。
4、通过RANSAC的5点算法来估计出两幅图像的本质矩阵。
5、通过本质矩阵进行估计R和t
6、对尺度信息进行估计,最终确定旋转矩阵和平移向量
实现视觉里程计


实现的过程
![]()
这里 定义相机图片宽度和高,焦距和相机饿中心点。


枚举名:FrameStage
如果枚举没有初始化, 即省掉”=整型常数”时, 则从第一个标识符开始,依次赋给标识符0, 1, 2, …。但当枚举中的某个成员赋值后, 其后的成员按依次 加1的规则确定其值。
向这个文件中输出数据
std::ofstream out("position.txt");
- 1
- 1
int font_face=cv::FONT_HERSHEY_PLAIN;
- 1
- 1
FONT_HERSHEY_PLAIN的值就是1
cv::namedWindow("abc",cv::WINDOW_AUTOSIZE);
- 1
- 1
自动调节窗口的大小。这里只是定义了窗口的名字,但是并没有把他显示出来。
cv::Mat::zeros(600,600,CV_8UC3)
- 1
- 1
CV_8UC3使用的Unsigned 8bits RGB3
Mat::zero返回指定大小的零数组
这里就是返回600*600的零数组,数组的类型是无符号类型的8bit RGB3类型
std::setw(6)填充6个空格
std::setfill(‘0’)填充0字符
// 导入图像
std::stringstream ss;
ss << "C:/dataset/00/image_1/"
<< std::setw(6) << std::setfill('0') << img_id << ".png";
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
cv::Mat img(cv::imread(ss.str().c_str(), 0));
- 1
- 1
将导入的图片转换成mat类型
这个ss.str().c_str(),
assert(!img.empty());
- 1
- 1
如果没有图像的话,就跳出循环
我第一次有这种感触,有的CPP文件,就像是一个大的存储容器,用来存储各种各样,在头文件当中没有办法实现的东西。但是你在看源码的过程当中,还是要从mian函数,从线程 的角度去看这些文件。
void addImage(const cv::Mat & img, int frame_id);
指的记住的东西就是 const cv::Mat &img.
/// 提供一个图像
void VisualOdometry::addImage(const cv::Mat& img, int frame_id)
{
//对添加的图像进行判断
if (img.empty() || img.type() != CV_8UC1 || img.cols != cam_->width() || img.rows != cam_->height())
throw std::runtime_error("Frame: provided image has not the same size as the camera model or image is not grayscale");
// 添加新帧
new_frame_ = img;
bool res = true;//结果状态
if (frame_stage_ == STAGE_DEFAULT_FRAME)
res = processFrame(frame_id);
else if (frame_stage_ == STAGE_SECOND_FRAME)
res = processSecondFrame();
else if (frame_stage_ == STAGE_FIRST_FRAME)
res = processFirstFrame();
// 处理结束之后将当前帧设为上一处理帧
last_frame_ = new_frame_;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
这里要抛出一个异常
throw std::runtime_error("sdfdff")
- 1
- 1
然后判断一下
if (frame_stage_ == STAGE_DEFAULT_FRAME)
res = processFrame(frame_id);
else if (frame_stage_ == STAGE_SECOND_FRAME)
res = processSecondFrame();
else if (frame_stage_ == STAGE_FIRST_FRAME)
res = processFirstFrame();
- 1
- 2
- 3
- 4
- 5
- 6
- 1
- 2
- 3
- 4
- 5
- 6
bool VisualOdometry::processFrame(int frame_id)
{
double scale = 1.00;//初始尺度为1
featureTracking(last_frame_, new_frame_, px_ref_, px_cur_, disparities_); //通过光流跟踪确定第二帧中的相关特征
cv::Mat E, R, t, mask;
E = cv::findEssentialMat(px_cur_, px_ref_, focal_, pp_, cv::RANSAC, 0.999, 1.0, mask);
cv::recoverPose(E, px_cur_, px_ref_, R, t, focal_, pp_, mask);
scale = getAbsoluteScale(frame_id);//得到当前帧的实际尺度
if (scale > 0.1) //如果尺度小于0.1可能计算出的Rt存在一定的问题,则不做处理,保留上一帧的值
{
cur_t_ = cur_t_ + scale*(cur_R_*t);
cur_R_ = R*cur_R_;
}
// 如果跟踪特征点数小于给定阈值,进行重新特征检测
if (px_ref_.size() < kMinNumFeature)
{
featureDetection(new_frame_, px_ref_);
featureTracking(last_frame_, new_frame_, px_ref_, px_cur_, disparities_);
}
px_ref_ = px_cur_;
retur
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
void VisualOdometry::featureTracking(cv::Mat image_ref, cv::Mat image_cur,
std::vector
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
KLT属入光流法。就是将上一个帧的图像和这一帧的图像对比,发现图像序列在时间域上的变换。
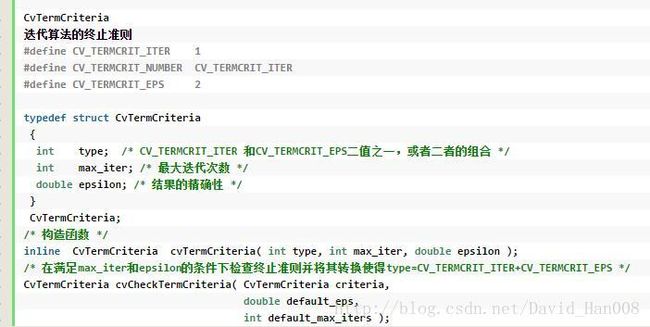
![]()
从这里可以看出,最大的迭代次数 和 结果的精准度,其实就是误差容限。这里其实就是实例化了一个对象,然后
赋予了初值。
这部分的例程可以参考这篇博客:
http://blog.csdn.net/liyuqian199695/article/details/49121525
cv::TermCriteria termcrit(cv::TermCriteria::COUNT+cv::TermCriteria::EPS, klt_max_iter, klt_eps);
- 1
- 1
我们只用关系这个klt_max_iter和klt_eps这两个参数,其他的参数不需要关注
cv::calcOpticalFlowPyrLK(image_ref, image_cur,
px_ref, px_cur,
status, error,
cv::Size2i(klt_win_size, klt_win_size),
4, termcrit, 0);
- 1
- 2
- 3
- 4
- 5
- 1
- 2
- 3
- 4
- 5
image_ref表示参考帧的(也就是上一帧的图像)
image_cur表示表示当前帧的图像 数据类型就是Mat类型
px_ref表示表示参考帧的特征点的光流 数据类型就是:std::vector
px_cur表示当真帧的特征点的光流
status表示 如果有特征流被发现,那么向量的元素都置为1,否则为0,那么这样的 他的数据类型是;std::vector
error表示输出错误的向量,数据类型std::vector
klt_win_size每个金字塔水平搜索窗口的尺寸 double类型 但是真正传递参数的时候,直接把他变成一个int类型,其实就cv::size2i(21.0,21.0),这么做的话其实就是,是一个矩形
下面这个4表示的是图像金字塔最大的层数是4层。
然后termcrit就是刚刚在上面实例化和初始化的参数,他表示的时判定准侧。
最后一个0表示的是标志位,
还有一个隐藏的数据,就是话精度的阈值是e^-4
通过这个函数,返回的话,可以直接找打KLT光流法的特征点
接下来,准备设置开始迭代
std::vector
- 1
- 2
- 1
- 2
将一个向量
disparities就是将所有的原来容器当中东西进行清除
disparities.clear();
- 1
- 1
下一条就是强制改变这个容器的大小
disparities.reserve(px_cur.size);
- 1
- 1
我觉他是要通过比较参考帧和当前帧的差异,然后通过这样的差异,来判断像素的位移。
然后然后现在开始循环
for (size_t i = 0; px_ref_it != px_ref.end(); ++i)
{
if (!status[i])
{
px_ref_it = px_ref.erase(px_ref_it);
px_cur_it = px_cur.erase(px_cur_it);
continue;
}
disparities.push_back(norm(cv::Point2d(px_ref_it->x - px_cur_it->x, px_ref_it->y - px_cur_it->y)));
++px_ref_it;
++px_cur_it;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
如果当前的状态不是1的话,,那么就从这两个容器中删除这些不相互匹配的元素
然后continue,继续执行
然后对每个像素都这么执行,
然后就是对每个disparities进行
然后就是这个里面的函数,进行平方,举个例子norm(3,4)=25,也就是说3的平方+4的平方=25
这样就实现了一个完整的跟随,从当真帧和参考帧当中
顺便看一个特征点的提取
void VisualOdometry::featureDetection(cv::Mat image, std::vector
- 1
- 1
可以看出输入的图像,和特征点
,
可以看出,这个视觉里程计利用使用的FAST进行提取的焦点
std::vector
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
然后将找到的特征点,给了这个时候输入的图像,也就是px_vec
cv::KeyPoint::convert(keypoints, px_vec);
- 1
- 1
然后我
bool VisualOdometry::processFrame(int frame_id)
{
double scale = 1.00;//初始尺度为1
featureTracking(last_frame_, new_frame_, px_ref_, px_cur_, disparities_); //通过光流跟踪确定第二帧中的相关特征
cv::Mat E, R, t, mask;
E = cv::findEssentialMat(px_cur_, px_ref_, focal_, pp_, cv::RANSAC, 0.999, 1.0, mask);
cv::recoverPose(E, px_cur_, px_ref_, R, t, focal_, pp_, mask);
scale = getAbsoluteScale(frame_id);//得到当前帧的实际尺度
if (scale > 0.1) //如果尺度小于0.1可能计算出的Rt存在一定的问题,则不做处理,保留上一帧的值
{
cur_t_ = cur_t_ + scale*(cur_R_*t);
cur_R_ = R*cur_R_;
}
// 如果跟踪特征点数小于给定阈值,进行重新特征检测
if (px_ref_.size() < kMinNumFeature)
{
featureDetection(new_frame_, px_ref_);
featureTracking(last_frame_, new_frame_, px_ref_, px_cur_, disparities_);
}
px_ref_ = px_cur_;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
featureTracking(last_frame_, new_frame_, px_ref_, px_cur_, disparities_); //通过光流跟踪确定第二帧中的相关特征
- 1
- 1
找本质矩阵,以及从本质矩阵中,恢复出R和t。
E = cv::findEssentialMat(px_cur_, px_ref_, focal_, pp_, cv::RANSAC, 0.999, 1.0, mask);
cv::recoverPose(E, px_cur_, px_ref_, R, t, focal_, pp_, mask);
- 1
- 2
- 1
- 2
输入当前帧的Id
double VisualOdometry::getAbsoluteScale(int frame_id)
- 1
- 1
double VisualOdometry::getAbsoluteScale(int frame_id)
{
std::string line;
int i = 0;
std::ifstream ground_truth("C:/dataset/00/00.txt");
double x = 0, y = 0, z = 0;
double x_prev, y_prev, z_prev;
// 获取当前帧真实位置与前一帧的真实位置的距离作为尺度值
if (ground_truth.is_open())
{
while ((std::getline(ground_truth, line)) && (i <= frame_id))
{
z_prev = z;
x_prev = x;
y_prev = y;
std::istringstream in(line);
for (int j = 0; j < 12; j++) {
in >> z;
if (j == 7) y = z;
if (j == 3) x = z;
}
i++;
}
ground_truth.close();
}
else {
std::cerr<< "Unable to open file";
return 0;
}
return sqrt((x - x_prev)*(x - x_prev) + (y - y_prev)*(y - y_prev) + (z - z_prev)*(z - z_prev));
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
这个函数的目的获取当前帧实际的尺度,我觉得是为了消除测量误差
输入这个文件
std::ifstream ground_truth("C:/dataset/00/00.txt");
- 1
- 1
将当前帧帧和前一帧实际位置的距离的尺度值
std::getline(ground_truth, line)) && (i <= frame_id)
- 1
- 1
用于读入字符 将你读入的字符存储到line当中,
如果geitline没有读入字符,将返回false,可用于判断文件结束
这里的i++肯定是对下一帧的图像进行循环
这里我也不清楚为什么要如果是是j=7,我看出来了,这是有两个循环。
返回的数值是一个误差尺度,就是就是一个的模值。
然后我们接着主线路走,在处理当前帧的时候,那么我已通过getsolutescale得到真实的尺度,如果这个尺度比0.1小的话,呢么可能这个数值是有问题的。那么我们就不要这个数值。然后这个值比0.1大的话,我们就更新一下现在的平移向量和旋转矩阵。


然后我们将当前帧赋值给参考帧,完成一次迭代更新。
最后我们回到主线程当中。也就是addImage当中,会发现,如果当前帧的状态等对
STAGE_DEFAULT_FRAME,那么我们就将这个处理的过程赋值给res。否则的话,我们就认为是其他帧。其实总共这里里面有3种帧。第一帧,第二帧,第一帧到第二帧都过渡帧,我们通过这个过渡帧,将第一帧和第二帧联系起来。
bool VisualOdometry::processSecondFrame()
{
featureTracking(last_frame_, new_frame_, px_ref_, px_cur_, disparities_); //通过光流跟踪确定第二帧中的相关特征
// 计算初始位置
cv::Mat E, R, t, mask;
E = cv::findEssentialMat(px_cur_, px_ref_, focal_, pp_, cv::RANSAC, 0.999, 1.0, mask);
cv::recoverPose(E, px_cur_, px_ref_, R, t, focal_, pp_, mask);
cur_R_ = R.clone();
cur_t_ = t.clone();
frame_stage_ = STAGE_DEFAULT_FRAME;// 设置状态处理默认帧
px_ref_ = px_cur_;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
然后我们分析一下第二帧。第二针当中。我们就是对frame_stage进行一种状态的赋值。他的数据类型是:FrameStage frame_stage_; //!< 当前为第几帧
cur_R_ = R.clone();
cur_t_ = t.clone();
frame_stage_ = STAGE_DEFAULT_FRAME;// 设置状态处理默认帧
px_ref_ = px_cur_;
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
将旋转矩阵做了替换
同时,我们看一下是如何处理第一帧的
bool VisualOdometry::processFirstFrame()
{
// 对当前帧进行特征检测
featureDetection(new_frame_, px_ref_);//第一帧计算出来的特征,为参考特征点
// 修改状态,表明第一帧已经处理完成
frame_stage_ = STAGE_SECOND_FRAME;
return true;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
在这里我们给图像的ID的最大值只是2000.现在我最好奇就是这里的文件,导入的路径。
我们通过addimge这个函数,将每一帧的图像和他对应ID匹配起来。
然后,通过设置不同的标志位,从而进行区分。
我们通过getCurrent来返回当真当前帧的平移量。
我们获得饿平移量。然后分别赋值给x,y,z

同时我们进行的输出,这样就知道平移量是怎么情况。
随后我们想要着这条路画出来。那么首先将这个x转化成int类型,然后这里的300和100表示的在像素中起始点的坐标,我们不希望将从一个平面当中的3来画出来。所有我们就移动了坐标轴。
circle这个,那么他的原理就是,第一个参数,表示要话的图像,第二个即使中心点,这个地方就是点饿坐标。然后就是点的半径,然后其实你可以选择用实心来画这个圆。然后选择线的颜色,选的线宽。然后就是一些默认饿参数,就可以了。
cv::Mat traj = cv::Mat::zeros(600, 600, CV_8UC3);// 用于绘制轨迹
从这个地方来看的,这个是一个空白的画布。就像是我们在视频当中看到黑色的画布。
我们在这里设置线的半径是1,线宽是2,颜色是红色。
然后我们接着画出一个矩形。准确的的说,就是一个实心的矩形,不就是一条直线么。然后我们输出一些文本,然后们就是通过sprintf输出一些东西。然后就是putText将一些文本弄出来,同时就是设置一些线宽什么乱七八糟的。哈哈。我们在将两个前面我们定义的namedwindow的东西输出出来。
然后我们将当时实例化的东西,释放到内存,同时关闭当当时打开的一些东西。并且将终端窗口用getchar()进行暂停。基本上这个这个视觉里程计的代码我就分析完毕了。
总体来看,就是的通过FAST进行焦点检测。然后通过光流法进行对特征点的提取和跟踪,然后通过处理帧,当前帧的参考帧,这三帧的相互配合,处理,在这个过程中我自己的收获,就是发现,原来看源码不是一个Cpp,一个cpp的看,而是通过一条清晰的主线,一条主线 ,一条主线的进行分析,然后当到进程和线程的一些东西的时候,顺着线程和进程的一条一条的走下去。然后很多人都是在头文件中声明很多东西,然后在cpp文件当中实现很多东西。
视觉slam第8讲 视觉里程计
特征点法的缺陷:
1、关键点的提取和描述子的计算都很耗时间
2、我们总是想用特征点来代替整个图像,导致很多图像的信息没有被使用。
3、相机运动的那么没有很多特征点的地方,例如白墙。
直接法 从大的方面 根据图像的灰度信息来计算相机的运动。
使用特征法估计相机运动的,我们是吧特征点看做固定在三维空间的不动点。根据他们在相机中的投影位置,通过最小化重投影误差(Reprojection error)来优化相机的运动。在直接法当中,我们是通过最小化光度误差(Photometric error)
光流(optical flow)
光流描述了像素在图像中的运动。计算部分像素称为稀疏光流,计算所有像素称为稠密光流。稀疏光流是以Lucas-Kanada光流为代表,并在SLAM当中用于跟踪特征点的位置。
灰度不变假设:同一个空间点的像素的灰度值,在各个图像中是固定不变的。在LK光流中,我们假设某一个窗口内的像素具有相同的运动。我感觉看下来,光流法还是提取特征。
直接法 完全依靠优化来求解相机的位姿。像素梯度引导着优化的方向。如果想要得到正确的优化结果,就必须保证大部分像素梯度能够把优化引导到正确的方向。
直接法的优点:
1、可以省去计算特征点和描述子的时间
2、只要求有像素的梯度就可以。
3、可以构建半稠密乃至稠密的地图
缺点:
1、非凸性,直接法完全依靠梯度搜索,降低目标函数来计算相机的位姿。
2、单个像素没有区分度
- 顶
- 1
- 踩
- 1
- 上一篇ROS学习笔记(四) 先锋机器人跟随
- 下一篇word备忘
- • MATLAB常用的快捷键
- • SLAM方法汇总
- • halcon中的分类器之GMM算子全讲解
- • 【分类器】常用的聚类算法-K-means
- • 浅谈 “矩”的概念
- • vslam: 扫盲之旅
- • 一起做RGB-D SLAM (4)
- • 增强现实技术漫谈(续)——研究内容全面解析
- • OpenCV学习笔记(14)利用Matlab查看双目视觉景深效果
- • 《Oracle编程艺术》学习笔记(29)-临时表和CBO
- 猜你在找
- 机器学习之概率与统计推断
- 机器学习之数学基础
- 机器学习之凸优化
- 机器学习之矩阵
- 响应式布局全新探索
- 探究Linux的总线、设备、驱动模型
- 深度学习基础与TensorFlow实践
- 深度学习之神经网络原理与实战技巧
- 前端开发在线峰会
- TensorFlow实战进阶:手把手教你做图像识别应用
















暂无评论