剑指offer题解（八）：c++&java

二叉树的镜像

题目描述

操作给定的二叉树，将其变换为源二叉树的镜像。

解题思路

c++

class Solution {
private:
    void swapfun(TreeNode *root)
    {
        TreeNode *t = root->left;
        root->left = root->right;
        root->right = t;
    }
public:
    void Mirror(TreeNode *pRoot) {
        if(pRoot == NULL)
            return;
        swapfun(pRoot);
        Mirror(pRoot->left);
        Mirror(pRoot->right);

    }
};

java

public void Mirror(TreeNode root) {
    if (root == null)
        return;
    swap(root);
    Mirror(root.left);
    Mirror(root.right);
}

private void swap(TreeNode root) {
    TreeNode t = root.left;
    root.left = root.right;
    root.right = t;
}

对称的二叉树

题目描述

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

解题思路

c++

class Solution {
private:
    bool duicheng(TreeNode* t1, TreeNode* t2)
    {
        if(t1==NULL&&t2==NULL)
            return true;
        if(t1==NULL||t2==NULL)
            return false;
        if(t1->val!=t2->val)
            return false;
        return duicheng(t1->left,t2->right)&&duicheng(t1->right,t2->left);


    }
public:
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(pRoot==NULL)
            return true;
        return duicheng(pRoot->left,pRoot->right);

    }

};

java

boolean isSymmetrical(TreeNode pRoot) {
    if (pRoot == null)
        return true;
    return isSymmetrical(pRoot.left, pRoot.right);
}

boolean isSymmetrical(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null)
        return true;
    if (t1 == null || t2 == null)
        return false;
    if (t1.val != t2.val)
        return false;
    return isSymmetrical(t1.left, t2.right) && isSymmetrical(t1.right, t2.left);
}

顺时针打印矩阵

题目描述

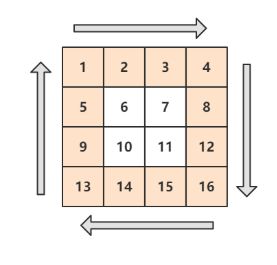
下图的矩阵顺时针打印结果为：1, 2, 3, 4, 8, 12, 16, 15, 14, 13, 9, 5, 6, 7, 11, 10

java

public ArrayList printMatrix(int[][] matrix) {
    ArrayList ret = new ArrayList<>();
    int r1 = 0, r2 = matrix.length - 1, c1 = 0, c2 = matrix[0].length - 1;
    while (r1 <= r2 && c1 <= c2) {
        for (int i = c1; i <= c2; i++)
            ret.add(matrix[r1][i]);
        for (int i = r1 + 1; i <= r2; i++)
            ret.add(matrix[i][c2]);
        if (r1 != r2)
            for (int i = c2 - 1; i >= c1; i--)
                ret.add(matrix[r2][i]);
        if (c1 != c2)
            for (int i = r2 - 1; i > r1; i--)
                ret.add(matrix[i][c1]);
        r1++; r2--; c1++; c2--;
    }
    return ret;
}

c++

class Solution {
public:
    vector<int> printMatrix(vector<vector<int>> matrix) {
        int row=matrix.size();
        int col=matrix[0].size();
        vector<int> result;
        if(row==0||col==0)
            return result;
        int left=0,right=col-1,top=0,btm=row-1;
        while(left<=right&&top<=btm)
            {
            for(int i=left;i<=right;i++)
                result.push_back(matrix[top][i]);
            if(topfor(int i=top+1;i<=btm;i++)
                    result.push_back(matrix[i][right]);
            if(topfor(int i=right-1;i>=left;i--)
                    result.push_back(matrix[btm][i]);
            if(top+1for(int i=btm-1;i>=top+1;i--)
                    result.push_back(matrix[i][left]);
            left++;right--;top++;btm--;
        }
        return result;
    }
};

包含 min 函数的栈

题目描述

定义栈的数据结构，请在该类型中实现一个能够得到栈最小元素的 min 函数。

c++

class Solution {
public:
    void push(int value) {
        st.push(value);
        if(smin.empty())
            smin.push(value);
        if(smin.top()>value)
            smin.push(value);
    }
    void pop() {
        if(smin.top()==st.top())
            smin.pop();
        st.pop();
    }
    int top() {
        return st.top();
    }
    int min() {
        return smin.top();
    }
    private:
    stack<int> st;
    stack<int> smin;
};

java

private Stack stack = new Stack<>();
private Stack minStack = new Stack<>();

public void push(int node) {
    stack.push(node);
    minStack.push(minStack.isEmpty() ? node : Math.min(minStack.peek(), node));
}

public void pop() {
    stack.pop();
    minStack.pop();
}

public int top() {
    return stack.peek();
}

public int min() {
    return minStack.peek();
}