R语言Box-Cox变换与多重共性线
Box-Cox
在做回归分析时,通常假设回归方程的残差具有有齐性,即等方差。如果残差不满足齐性,其结果会出现问题,前面介绍了一种加权的最小二乘法了,这里介绍数据变化方法。
在出现异方差的情况下(残差发散),做Box-Cox
变换可以回归方程残差保持齐性。

Box-Cox主要有两项工作,第一是做变换,第二是确定拉姆达的值。要用最大似然估计才能确定拉姆达的值,要加载(MASS)包)
Y人均购买量(元)与X为家庭人均收入(元)
##%% 输入数据, 作回归方程
X<-scan()
679 292 1012 493 582 1156 997 2189 1097 2078
1818 1700 747 2030 1643 414 354 1276 745 435
540 874 1543 1029 710 1434 837 1748 1381 1428
1255 1777 370 2316 1130 463 770 724 808 790
783 406 1242 658 1746 468 1114 413 1787 3560
1495 2221 1526
Y<-scan()
0.79 0.44 0.56 0.79 2.70 3.64 4.73 9.50 5.34 6.85
5.84 5.21 3.25 4.43 3.16 0.50 0.17 1.88 0.77 1.39
0.56 1.56 5.28 0.64 4.00 0.31 4.20 4.88 3.48 7.58
2.63 4.99 0.59 8.19 4.79 0.51 1.74 4.10 3.94 0.96
3.29 0.44 3.24 2.14 5.71 0.64 1.90 0.51 8.33 14.94
5.11 3.85 3.93
lm.sol<-lm(Y~X); summary(lm.sol)
Call:
lm(formula = Y ~ X)
Residuals:
Min 1Q Median 3Q Max
-4.1399 -0.8275 -0.1934 1.2376 3.1522
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.8313037 0.4416121 -1.882 0.0655 .
X 0.0036828 0.0003339 11.030 4.11e-15 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.577 on 51 degrees of freedom
Multiple R-squared: 0.7046, Adjusted R-squared: 0.6988
F-statistic: 121.7 on 1 and 51 DF, p-value: 4.106e-15
加载MASS程
library(MASS)
作图, 共4张
op <- par(mfrow=c(2,2), mar=.4+c(4,4,1,1), oma= c(0,0,2,0))
第1张, 残差与预测散点图
plot(fitted(lm.sol), resid(lm.sol),
cex=1.2, pch=21, col="red", bg="orange",
xlab="Fitted Value", ylab="Residuals")
第2张, 确定参数lambda
boxcox(lm.sol, lambda=seq(0, 1, by=0.1))
Box-Cox变换后, 作回归分析
lambda<- 0.55; Ylam<- (Y^lambda-1)/lambda
lm.lam<-lm(Ylam~X); summary(lm.lam)
第3张, 变换后残差与预测散点图
plot(fitted(lm.lam), resid(lm.lam),
cex=1.2, pch=21, col="red", bg="orange",
xlab="Fitted Value", ylab="Residuals")
第4张, 回归曲线和相应的散点
beta0<-lm.lam$coefficients[1]
beta1<-lm.lam$coefficients[2]
curve((1+lambda*(beta0+beta1*x))^(1/lambda),
from=min(X), to=max(X), col="blue", lwd=2,
xlab="X", ylab="Y")
points(X,Y, pch=21, cex=1.2, col="red", bg="orange")
mtext("Box-Cox Transformations", outer = TRUE, cex=1.5)
par(op)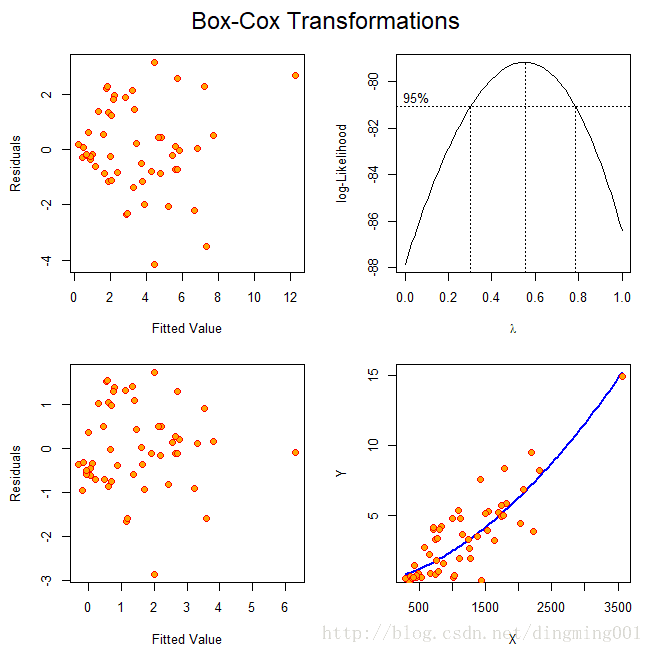
从第一张图可以看出,原始数据的残差图成喇叭口,属于异方差情况,要做Box-Cox变换,在变换前先得到参数lambda
从第二张图可以看出,lambda = 0.55,对数似然函数达到最大值
从第三张图可以看出,进行变换之后,在做残差分析,画出残差分布图,喇叭口有很大改善。
第四张图给出曲线图和对应的散点图
Y = (1+lambda*b +lambda*b1*X)^1/lambda多重共线性
当自变量彼此相关时,估计的效应会用于模型中其它的自变量而改变值,甚至符号。故在分析时,了解自变量关系的影响很重要,这一问题称为共性或者多重共线性。
进口总额Y与三个自变量:国内生产总值x,存储量X2,总消费X3的关系
france<-data.frame(
x1 = c(149.3, 161.2, 171.5, 175.5, 180.8, 190.7,
202.1, 212.4, 226.1, 231.9, 239.0),
x2 = c(4.2, 4.1, 3.1, 3.1, 1.1, 2.2, 2.1, 5.6, 5.0,
5.1, 0.7),
x3 = c(108.1, 114.8, 123.2, 126.9, 132.1, 137.7,
146.0, 154.1, 162.3, 164.3, 167.6),
y = c(15.9, 16.4, 19.0, 19.1, 18.8, 20.4, 22.7,
26.5, 28.1, 27.6, 26.3)
)
lm.sol<- lm(y~1+x1+x2+x3, data=france)
lm.sum<-summary(lm.sol)
coef(lm.sum)
Estimate Std. Error t value Pr(>|t|)
(Intercept) -10.12798816 1.21215996 -8.3553231 6.899183e-05
x1 -0.05139616 0.07027999 -0.7313058 4.883443e-01
x2 0.58694904 0.09461842 6.2033274 4.438135e-04
x3 0.28684868 0.10220811 2.8025157 2.627710e-02虽然方程的系数通过了检验,但发现并不合理,Y代表进口量,x1代表国内生产总值,两者应该是正相关,出现负号的原因是,三者存在多重共性线的关系。用程序检验。
X<-as.matrix(france[1:3])
min(eigen(cor(X))$values)
[1] 0.002690889说明三个自变量存在多重共线性关系
岭估计
当矩阵存在多重共线性关系时,最小二乘估计的性质不够理想。k>0为选参数,称为岭参数和偏差数。k=0为最小二乘估计,最小二乘估计是岭估计中的一个估计。
library(MASS)
lm.rid<-lm.ridge(y~1+x1+x2+x3, data=france,
lambda=seq(0, 0.2, length=50))
par(mai=c(0.9, 0.9, 0.2, 0.2))
plot(lm.rid)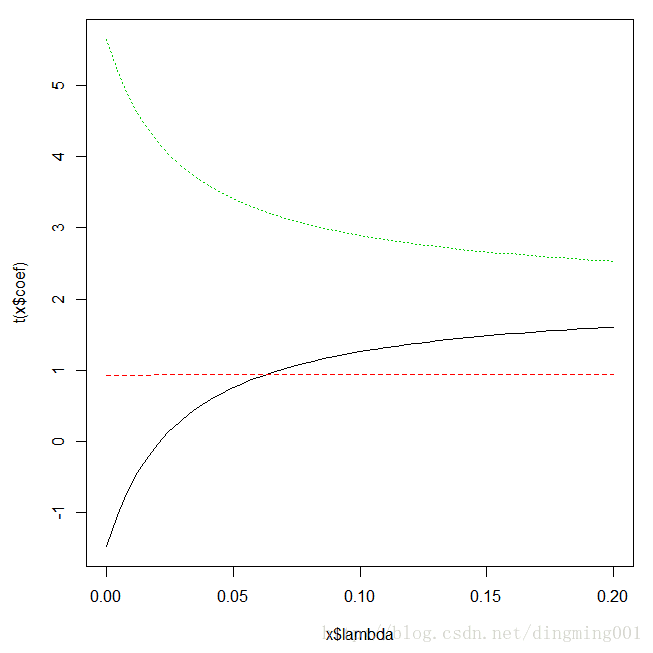
法国经济分析岭迹曲线
lamda取值大于0,这样才有“惩罚”的意义。一般选取的lamda值为岭迹线从陡峭转为平缓的位置,但依据实际问题而定。取k=0.04
lm.ridge(y~1+x1+x2+x3, data=france, lambda=0.04)
x1 x2 x3
-9.4956573 0.0198393 0.5976872 0.182875 三个系数都为正,此模型合理一些。