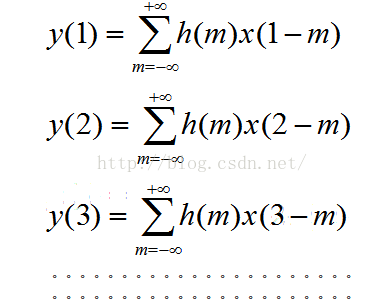FIR滤波器的DSP实现
试看数字滤波如何规避硬件设计
一,实践意义
我想这绝对是一个让人眼前一亮的例子,为什么这么讲?因为但凡搞过硬件的人都知道一个事实,硬件滤波器做起来是一件很麻烦的事情。可以说5000系列DSP从这一刻起开始突显它的真正的价值了。很多同学问我DSP学起来到底有什么用,如果非要有一个开始的话,我想数字滤波便是它的第一个非常有用的功能。至少这次实验课让我心潮澎湃,终于见识到了软件滤波的庐山真面目和它神奇的功效。以一言蔽之,软件滤波的出现是一件具有划时代意义的事情,因为它的出现让我们规避了复杂而又功能不完美的硬件滤波器的设计。
二,实验概述
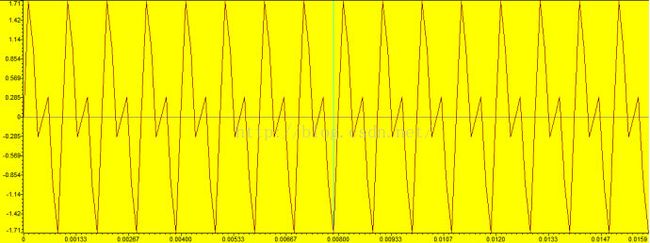
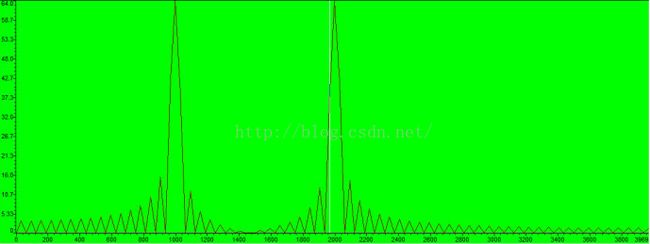
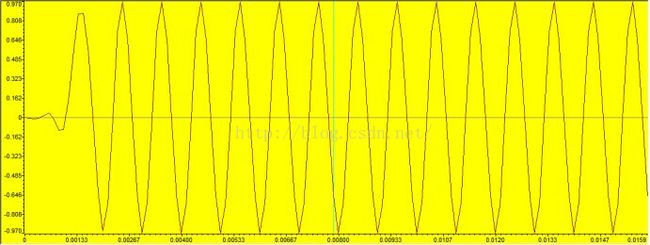
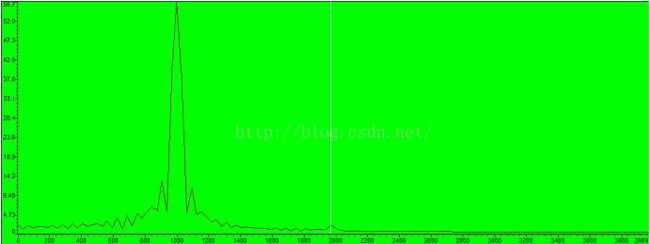
本次实例采用一个利用Matlab生成的FIR数字低通滤波器系数表直接应用与DSP程序中,我们将在DSP程序里面用已知的输入信号,输入信号包含两个频率成分,1000Hz,2000Hz。让输入信号经过一个截止频率为1500Hz的FIR低通滤波器,然后观察输入输出波形和频谱。整个过程不会涉及到实体滤波器的任何东西,但是最终会发现,利用算法实现的这个信号软处理过程完全实现了滤波的功效。
三,实验步骤
1. 假定我们已经利用Matlab设计好了一个20阶的FIR低通滤波器,此低通滤波器的截止频率为1500Hz。滤波器系数表如下:
FIR_LPF[21]={
-0.001806524723551,-0.003360662865095,2.461716477557e-18, 0.011364134676,
0.01497353758673, -0.01319873582525, -0.05446122716448, -0.03301236910014,
0.1029885989805, 0.288399704569, 0.3762270877324, 0.288399704569,
0.1029885989805, -0.03301236910014, -0.05446122716448, -0.01319873582525,
0.01497353758673, 0.011364134676,2.461716477557e-18,-0.003360662865095,
-0.001806524723551
};
关于这个FIR系数表的产生方法详见我在Matlab栏的文章---FDATOOL设计滤波器一文中的介绍,这里不再赘述。
2. 在CCS建立工程,编译,装载,运行。这个过程也不再赘述,详见文章后面附录中的主程序,cmd文件,当然本工程还是不能缺少rts55.lib这个库文件。
3. 观察输入信号input[128]数组的时域波形如下:
四,数字滤波的原理
也许这正是数字滤波的魅力所在吧,数字滤波通过软件程序对数字信号处理的过程完全规避了硬件。
整个处理过程有一个比较关键的地方在于,我们是如何通过DSP的程序来实现输入信号经过滤波器这个过程的呢?习惯了频域分析的我们知道信号经过滤波器的过程实际上是频域特性相乘的关系,而在这个地方因为已经知道了FIR滤波器的系数表,输入信号的时间采样值,所以我们采用的是离散信号线性卷积的过程。这个过程可以用C语言嵌套for循环很轻松的实现。
离散信号线性卷积的公式如下:
把这一过程拆开,具体到输出信号的每一个点,即n值具体化:
一般来讲,我们要处理的两个信号都是有限点数。并且我们是以数组形式来存放他们的数值的,所以脚标引用一般都不会有负值,最小起点都是0。
为了便于理解这个离散卷积的高级语言实现,我建议最好不要死扣《信号与系统》里面的翻转,叠加过程,直接从上面表达式入手,注意上面表达式还可以接着把求和负号拆开,这样以来计算过程便很明了。
假定h(n)的长度为N1,x(n)的长度为N2。利用外层循环控制n,内层循环控制m的思路可以把上面的卷积过程表示成如下的C代码。
s=0;
for(n=0;n
好了,这样的代码就实现了信号x(n)和h(n)的卷积过程了。请仔细体会上面第二层for循环的控制条件,它非常有助于理解这个卷积过程。
五,总结
数字滤波器在DSP内部的实现机制其实是很简单的,利用高级程序语言将已知的时域信号采样值和滤波器的系数进行卷积即可。只是这个过程确实为信号处理带来了非常大的方便,因为它告别了传统的硬件滤波器,所以这必定是个非常有用的技能。
六,程序清单
//1. 主程序FIR.c
#include
#include
#define order 21
#define N 128
#define pi 3.14159265358979323846
float FIR_LPF[order] = {
-0.001806524723551,-0.003360662865095,2.461716477557e-18, 0.011364134676,
0.01497353758673, -0.01319873582525, -0.05446122716448, -0.03301236910014,
0.1029885989805, 0.288399704569, 0.3762270877324, 0.288399704569,
0.1029885989805, -0.03301236910014, -0.05446122716448, -0.01319873582525,
0.01497353758673, 0.011364134676,2.461716477557e-18,-0.003360662865095,
-0.001806524723551
};
float s;
int i,n;
float input[N],output[N];
int fs=8000;
int f1=2000;
int f2=1000;
#define w1 2*pi*f1/fs
#define w2 2*pi*f2/fs
void wavein()
{
for(n=0;n VECT
.trcinit: {} > PROG
.gblinit: {} > PROG
frt: {} > PROG
.text: {} > PROG
.cinit: {} > PROG
.pinit: {} > PROG
.sysinit: {} > PROG
.bss: {} > DATA
.far: {} > DATA
.const: {} > DATA
.switch: {} > DATA
.sysmem: {} > DATA
.cio: {} > DATA
.MEM$obj: {} > DATA
.sysheap: {} > DATA
.stack: {} > DATA
.sysstack {} > DATA
}