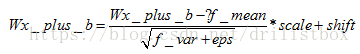TensorFlow入门深度学习--02.构建神经网络训练算法的步骤

文章列表
1.TensorFlow入门深度学习–01.基础知识. .
2.TensorFlow入门深度学习–02.基础知识. .
3.TensorFlow入门深度学习–03.softmax-regression实现MNIST数据分类. .
4.TensorFlow入门深度学习–04.自编码器（对添加高斯白噪声后的MNIST图像去噪）.
5.TensorFlow入门深度学习–05.多层感知器实现MNIST数据分类.
6.TensorFlow入门深度学习–06.可视化工具TensorBoard.
7.TensorFlow入门深度学习–07.卷积神经网络概述.
8.TensorFlow入门深度学习–08.AlexNet（对MNIST数据分类）.
9.TensorFlow入门深度学习–09.tf.contrib.slim用法详解.
10.TensorFlow入门深度学习–10.VGGNets16（slim实现）.
11.TensorFlow入门深度学习–11.GoogLeNet（Inception V3 slim实现）.
…

TensorFlow入门深度学习–02.构建神经网络训练算法的步骤

Tensflow训练神经网络可分为3个步骤：加载数据、设计网络模型、训练模型及评价模型。需要注意的是，Tensflow中定义的公式只是计算图(Computation Graph)，在执行代码时，计算还没有发生，只有等调用run方法并且feed数据后计算才真正执行。比如cross_entropy、train_step、accuracy等都是计算图中的节点，并不是数据结果，可以通过调用run方法执行这些节点或者说运算操作来获取结果。

2.1 加载数据

2.1.1 预加载数据

在TensorFlow图中定义常亮或变量来保存数据

x = tf.variable([3.0],tf.float32)
y = tf.constant([5.0],tf.float32)
z = tf.add(x,y)

预加载的数据直接嵌在数据图中，当训练数据很大是，很容易消耗内存

2.1.2 填充数据

利用会话run函数的参数填充数据。

x = tf.variable([3.0],tf.float32)
y = tf.placeholder(tf.float32) #占位符变量没有定义大小，因此在run中可以输入任意大小的数据
z = tf.add(x,y)
with tf.Session as sess:
    print(sess.run(feed_dict={y:[6.0]}))
    print('c=', sess.run(c,feed_dict={b:[1.0, 2.0]}))
    print('c=', sess.run(c,feed_dict={b:[[1.0, 2.0],[3.0, 4.0]]}))
    print('c', sess.run(c,feed_dict={b:np.array([[1.0, 2.0],[3.0, 4.0]])}))

填充方式也有数据量大、消耗内存的缺点，并且数据类型转换等中间环节也需要开销，这时可通过在队列中定义好文件读取的方法，让TensorFlow自己从文件中读取数据，并解码成可使用的样本集。

2.1.3 从文件读取数据

首先将样本数据写入TFRecords二进制文件，然后再从队列中读取数据。
读入数据并将其写入TFRecords

# -*- coding: utf-8 -*-
import os 
import tensorflow as tf 
from PIL import Image  
_int64_feature = lambda value: tf.train.Feature(int64_list=tf.train.Int64List(value=[value]))  
_bytes_feature = lambda value: tf.train.Feature(bytes_list=tf.train.BytesList(value=[value])) 
#图片路径
cwd = 'C:\\Users\\Administrator\\Pictures\\new\\'
#tfrecord文件保存路径
filepath = 'C:\\Users\\Administrator\\Pictures\\tfrecord\\'
#第几个图片
num = 0
#tfrecords格式文件名
ftrecordfilename = ("traindata.tfrecords-%.3d" % 0)
writer= tf.python_io.TFRecordWriter(filepath+ftrecordfilename)
#exampleNum = tf.train.Example(features=tf.train.Features(feature={
#    'imageNum': _int64_feature(3)
#})) 
#writer.write(exampleNum.SerializeToString())  #序列化为字符串
for img_name in os.listdir(cwd): 
    num=num+1
    img_path = cwd+img_name #每一个图片的地址
    img=Image.open(img_path,'r')
    size = img.size
    print(size)
    img_raw=img.tobytes()#将图片转化为二进制格式
    example = tf.train.Example(features=tf.train.Features(feature={
        'label'     : _int64_feature(1),
        'img_raw'   : _bytes_feature(img_raw),
        'img_width' : _int64_feature(size[0]),
        'img_height': _int64_feature(size[1])
    })) 
    writer.write(example.SerializeToString())  #序列化为字符串
writer.close()

从队列中读取数据

# -*- coding: utf-8 -*-
import tensorflow as tf 
from PIL import Image  
import matplotlib.pyplot as plt
_int64_feature = lambda value: tf.train.Feature(int64_list=tf.train.Int64List(value=[value]))  
_bytes_feature = lambda value: tf.train.Feature(bytes_list=tf.train.BytesList(value=[value])) 

#写入图片路径
swd = 'C:\\Users\\Administrator\\Pictures\\out\\'
#TFRecord文件路径
data_path = 'C:\\Users\\Administrator\\Pictures\\tfrecord\\traindata.tfrecords-000'
# 获取文件名列表
data_files = tf.gfile.Glob(data_path)
print(data_files)
# 文件名列表生成器
filename_queue = tf.train.string_input_producer(data_files,shuffle=True) 
reader = tf.TFRecordReader()
_, serialized_example = reader.read(filename_queue)   #返回文件名和文件
#从TFRecords文件中读取数据， 可以使用tf.parse_single_example解析器, 将Example协议内存块(protocol buffer)解析为张量。 
features = tf.parse_single_example(serialized_example, features={
                                       'label'     : tf.FixedLenFeature([], tf.int64),
                                       'img_raw'   : tf.FixedLenFeature([], tf.string),
                                       'img_width' : tf.FixedLenFeature([], tf.int64),
                                       'img_height': tf.FixedLenFeature([], tf.int64),
                                   })  #取出包含image和label的feature对象
#tf.decode_raw可以将字符串解析成图像对应的像素数组
image = tf.decode_raw(features['img_raw'], tf.uint8)
height = tf.cast(features['img_height'],tf.int32)
width = tf.cast(features['img_width'],tf.int32)
label = tf.cast(features['label'], tf.int32)
channel = 3
image = tf.reshape(image, [height,width,channel])
with tf.Session() as sess: #开始一个会话
    sess.run(tf.global_variables_initializer())
    coord=tf.train.Coordinator() #启动多线程
    threads= tf.train.start_queue_runners(coord=coord)
    for i in range(3):
        plt.imshow(image.eval())
        plt.show()
        single,l = sess.run([image,label])#在会话中取出image和label
        img=Image.fromarray(single, 'RGB')#这里Image是之前提到的
        img.save(swd+str(i)+'_''Label_'+str(l)+'.jpg')#存下图片
    coord.request_stop()
    coord.join(threads)

import tensorflow as tf
# 输入数据
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("./../../MNISTData", one_hot=True)

2.2 网络模型设计

2.2.1 超参数设置

在加载数据的过程中需定义模型的超参数（比如总迭代次数、学习率、小批量数据的大小、Dropout的概率等）、数据的输入（输入维度、分类问题中输出标记的维度）

# 定义网络的超参数
learning_rate = 0.001
training_iters = 200000
batch_size = 128
display_step = 5
# 输入及输出标记的维度、占位符等
n_input = 784 # 输入的维度 (img shape: 28*28)
n_classes = 10 # 标记的维度 (0-9 digits)
dropout = 0.75 # Dropout的概率，输出的可能性
x = tf.placeholder(tf.float32, [None, n_input])
y = tf.placeholder(tf.float32, [None, n_classes])
keep_prob = tf.placeholder(tf.float32) #dropout (keep probability)

2.2.1.1 以命令行参数的方式设置超参数

利用tf.app.flags可以实现指定参数的命令行设置，多说无益，直接上代码：
在untitled.py文件写入如下代码

import tensorflow  as tf  
FLAGS=tf.app.flags.FLAGS  
tf.app.flags.DEFINE_float('flag_float', 0.01, 'input a float')  
tf.app.flags.DEFINE_integer('flag_int', 400, 'input a int')  
tf.app.flags.DEFINE_boolean('flag_bool', True, 'input a bool')  
tf.app.flags.DEFINE_string('flag_string', 'yes', 'input a string')  
print(FLAGS.flag_float)  
print(FLAGS.flag_int)  
print(FLAGS.flag_bool)  
print(FLAGS.flag_string)

再在命令行中输入以下代码：

python untitled.py
python untitled.py --flag_int 1 --flag_bool True --flag_string 'sdfsdagsa' --flag_float 0.2

运行结果如下：

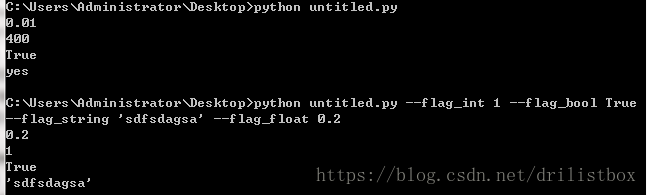
可见我们可以通过tf.app.flagsDEFINE_XXX来设定变量的值，并且该以这种方式定义的变量还可以通过命令行参数的方式来设置。当然定义好的变量可以直接通过赋值操作来改变其值，如：

FLAGS = tf.app.flags.FLAGS
FLAGS.flag_int = 5

2.2.2 激活函数

神经网络对非线性问题优异的解决能力来自于非线性激活函数，可以想象，如果激活函数全是线性的，那么层数再深的数神经网络也仅仅等价于单层网络。常见的激活函数有：阶跃激活函数、线性激活函数、tf.nn.sigmoid()、tf.nn.tanh()、tf.nn.relu()、Leaky ReLU、tf.nn.softmax()。

2.2.2.1 阶跃激活函数

阶跃激活函数用在感知机中：
• 由于该函数为二值输出，所以只能用于分类问题；
• 由于该函数不可导，使得感知机只能以误分类点个数为损失函数（详参https://blog.csdn.net/drilistbox/article/details/79341381），这也是感知机泛化能力较差的一个原因。

2.2.2.2 线性激活函数

线性激活函数用于简单的回归问题中，但用线性激活函数的话，深度学习中的多层就变得没有意义。

2.2.2.3 tf.sigmoid

sigmoid函数可表示为sigmoid(x) = 1/(1+exp(-x))：
优点：
• 由于sigmoid函数输出在0-1之间，符合概率输出的定义；
• sigmoid本身的非线性特性使其性能比线性激活函数y=x以及阶梯激活函数的功能要强很多，学习特征能力增强。
• 求导方便
缺点：
• 在饱和区内梯度较小
• 激活函数导数的最大值为0.25，使得网络层数较深时存在梯度消失问题。
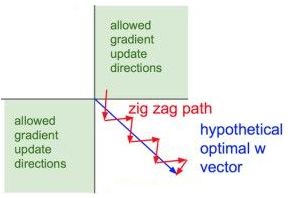
• 优化路径就很容易出现zigzag现象。由于sigmoid输出总是正数，对下图中的节点1和2求梯度，有：

式中x1和x2分别为节点1和2的输出，由于激活函数为sigmoid，所以x1和x2均大于0，结合上式知w1和w2的梯度同向，所以w1和w2的梯度向量只能在第1及第3象限，那么这时的优化路径就很容易出现zigzag现象（锯齿形波动）【详参斯坦福2017季CS231n深度视觉识别课程视频】。

tf.sigmoid的使用方法如下：
class=”python”>

import tensorflow as tf
Wx_plus_b = tf.Variable([[1,2],[3,4],[5,6]], dtype=tf.float64)
with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())
  print('output:', sess.run(tf.sigmoid(Wx_plus_b)))

别为：

2.2.2.4 tf.tanh

tf.tanh是tf.sigmoid的线性变换，所以sigmoid有的特性tanh都有。但由于tanh的输出在-1到+1之间，所以可以避免zigzag现象：
tf.tanh的使用方法同上，只要将其中的sigmoid改成tanh即可。tanh的形状与sigmoid类似，两者之间可通过平移及缩放而相互转换，例如另sigmoid(x) = 1/(1+exp(-x))，则tanh(x)= 2/(1+exp(-x*2))-1，tanh(x)输出区间在-1到1之间，所以可以避免zigzag现象，且其收敛速度比sigmoid快，但在饱和区内同样存在梯度较小的问题。

2.2.2.5 ReLU

其定义为f(x)=max(x,0)，tf.relu的使用方法同上，只要将其中的sigmoid改成relu即可。ReLU相对于sigmoid的好处主要有以下4点：
• 单侧抑制，ReLU有一半的可能性取值为0， 满足稀疏激活性（神经科学家分析大脑发现神经元编码的工作方式是稀疏的，推测大脑同时被激活的神经元只有1-4%）。
• 相对宽阔的兴奋边界（在输入大于0区间梯度都为1），减缓梯度消失现象
• 梯度计算更容易，Relu在输入小于0时硬饱和，在输入大于0时梯度为1，从而缓解了梯度消失问题。
缺点：
该函数在输入小于0的硬饱和可能导致对应的权重无法更新，从而进入“死忙区”。

2.2.2.6 Leaky ReLU

Leaky ReLU是为解决“ReLU死亡”问题的尝试。ReLU中当x<0时，函数值为0。而Leaky ReLU则是给出一个很小的负数梯度值，比如0.01。所以其函数公式为

有些研究者的论文指出这个激活函数表现很不错，但是其效果并不是很稳定。Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法PReLU，把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰。

2.2.2.7 Softplus

Softplus是ReLU的近似，其函数表达式为y=log(1+exp(x))，虽然softplus有单侧抑制，但是却没有稀疏的激活性。

2.2.2.8 SoftMax

softmax

2.2.3 全连接层

in_units = 784
h1_units = 300

2.2.3.1 输入项

x_fc = tf.placeholder(tf.float32, [None, 784])#输入数据的占位符

2.2.3.2 权重参数及偏置参数

(1)权重矩阵初始化为0
激活函数为sigmoid函数时，由于sigmoid函数在0附近最敏感，权重矩阵和偏置项可初始化为0
W_fc = tf.Variable(tf.zeros([h1_units, 10])) #第2层的权重矩阵
(2)权重矩阵,正太分布
W_fc = tf.Variable(tf.random_normal([in_units,hi_units],mean=0.0, stddev=0.1, dtype=tf.float32, seed=None, name=None))
(3)权重矩阵,带截断的正太分布
激活函数为ReLu时，需要使用正太分布给参数添加一点随机噪声，从而打破完全对称并避免0梯度
W_fc = tf.Variable(tf.truncated_normal([in_units, hi_units], stddev=0.1))
(1)0偏置项
激活函数为sigmoid函数时，由于sigmoid函数在0附近最敏感，权重矩阵和偏置项可初始化为0
b_fc = tf.Variable(tf.zeros([h1_units]))
(2)非0偏置项
激活函数为ReLu时，需给偏置项赋上小的非0值来避免死忙神经元(dead neuron)
b_ fc = tf.constant(0.1, shape=[in_channels])

2.2.3.3 激活函数及输出项

(1)o_fc = tf.nn.relu(tf.matmul(x_fc, W_fc) + bi) #激活函数为relu
(2)o_fc = tf.nn.softmax(tf.matmul(x_fc, W_fc) + b2) #激活函数为softmax
(3)o_fc = tf.nn.softmax(tf.matmul(x_fc, W_fc) + b2) #激活函数为softmax

2.2.4 卷积层

卷积层包含输入项、卷积核、激活函数及输出项，卷积核在图像上提取特征的动作称为padding，有same和valid这两种方式，卷积核移动步长stride不一定能整除输入项的维度，将不越过边缘的特征提取称为valid padding，提取出的特征维度小于输入项的维度；将越过边缘的特征提取称为same padding(越过的部分用0代替)，提取出的特征与输入项维度一致。

2.2.4.1 输入项

(1)

x = tf.placeholder(tf.float32, [None, 784])
x = tf.reshape(x, [-1, in_height, in_width, in_channels]) #前面的-1代表样本数量不定

(2)

 x = tf.placeholder(tf.float32, [batch, in_height, in_width, in_channels])#输入数据的占位符

2.2.4.2 卷积核定义

W = tf.truncated_normal([filter_height, filter_width, in_channels, out_channels], stddev=0.1)
b = tf.constant(0.1, shape=[in_channels])

2.2.4.3 节点输入

Net = tf.nn.conv2d (x, W, strides=[1, 1, 1, 1], padding='SAME') + b

式中b为偏执项，利用tf.nn.conv2d实现了二维卷积，其中x为输入图像，W为卷积核，strides=[]，padding有两种模式，即SAME和VALID，将不越过边缘的取样卷积称为VALID，此时输出尺寸=1+向下取整{(输入尺寸-卷积核宽度)/步长}；将越过边缘使得取样面积和输入图像面积一致的方式称为SAME，此时输出尺寸=向上取整(输入尺寸/步长)。

2.2.4.4 输出项定义

h_conv = tf.nn.relu(Net)

2.2.4.5 参数大小及所需算力FLOPS

Params = (filter_height*filter_width*in_channels + 1) *out_channels
FLOPS：每秒浮点运算次数，每秒峰值速度
FLOPS = out_height* out_width*Params
例如，某一卷积层输入图像大小为224*224*3，卷积核尺寸为11*11，步长为4，有96个卷积核，那么
Params = (11*11*3+1)*96/1000=34k
FLOPS = (224/4)* (224/4)* Params=102584384=102584384/100/100=105M

2.2.5 下采样层

h_pool = tf.nn.max_pool(x_ pool, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

由于深度神经网络包含许多全连接层、卷积层及下采样层，因此可以定义好相应层或系数的初始化函数以便重复使用。

2.2.6 分类函数

1. tf.nn.sigmoid_cross_with_logits(logits,targets,name=None)
   这个函数表示输出层的激活函数为sigmoid，损失函数为交叉熵。这样具有与输出误差呈线性关系的梯度项。由于其中包含了激活函数，所以在输出层中无需再次定义激活函数。
2. tf.nn.softmax(logits,dim=-1,name=None)
   计算：

2.2.7 技巧

2.2.7.1 网络深度的增加

深层网络可以逐层学习到原始数据的多种表达。网络深度的增加就是指隐藏层层数的增加，没有隐藏层的神经网络直接利用图像的像素点推断结果，没有特征抽象提取的过程。多层神经网络依靠隐藏层，每层隐藏层中的卷积核可以提取出各种形态的点、线等，然后更深的隐藏层可以将这些特征组合成更高阶的特征，从而实现精准的分类。而且这些高阶特征都是可以复用的，这样每一类的判别输出都共享这些高阶特征。
多个隐藏层的作用是逐层提取特征，比如第一层学习点和边的识别，第二层学习点和边的组合，从而获取轮廓、角等高阶特征，第3第4等更高层学习更高阶的具体物体识别特征。

2.2.7.2 权重初始化：Xavier初始化

权重初始化得太小会导致数据流在层间传递时逐渐缩小而难以产生作用，权重初始化得太大会导致数据流在层间传递时逐渐变大而导致发散和失效，而Xavier初始化的目的就是使得权重初始化值大小合适，其初始化得权重满足0均值，方差为2/(n_in+n_out)范围内的均匀分布或高斯分布

2.2.7.3 tf.nn.dropout

在训练时随机将部分节点置为0，可以制造随机性，防止过拟合；预测时保留全部数据来追求最好的预测性能

keep_prob = tf.placeholder(tf.float32)
hidden1_drop = tf.nn.dropout(hidden1, keep_prob)

2.2.7.4 L2正则化

在机器学习中，不论是分类还是回归任务，都可能因特征太多而导致过拟合，一般可以通过减少特征或者惩罚不重要特征的权重来缓解这个问题。但通常不知道如何设计合理的惩罚方法，正则化就是一种合理的惩罚特征权重的方法，即将特征权重的范数作为模型损失函数的一部分。
可以理解为，为了使用某个特征，需要付出损失函数的代价，除非这个特征非常有效，否则就被原有损失函数上增加的部分覆盖掉。具体地，用正则项表示使用特征付出的损失函数的代价，原有损失函数的大小表示当前特征的有效性，并用正则项系数来权衡两者之间的轻重，这样就可以筛选出有效的特征，减少无效的特征权重，从而防止过拟合。这也是奥卡姆剃刀法则，越简单的东西越有效。一般来说，L1正则会得到稀疏的特征权重，而L2正则会使特征的权重不会太大。
定义variable_with_weight_loss函数初始化权重矩阵，用shape定义权重矩阵维数，用stddev定义权重矩阵正太分布标准差，使用正则化系数wl控制正则项对损失函数的贡献，如果wl=0表示不对该层权重矩阵进行正则。利用tf.nn.l2_loss计算权重矩阵的L2范数，并利用tf.multiply获得考虑正则系数后的L2范数，最后利用tf.add_to_collection把weight_loss统一存到一个collection，并将该collection命名为weight_loss

def variable_with_weight_loss(shape, stddev, wl) : 
    var = tf.Variable( tf.truncated_normal(shape, stddev=stddev) ) 
    if wl is not None:
        weight_loss = tf.multiply( tf.nn.l2_loss(var), wl, name='weight_loss' )
        tf.add_to_collection( 'losses', weight_loss )
return var

卷积层权重矩阵初始化并对其正则化

weight1 = variable_with_weight_loss( shape=[5,5,3,64], stddev=5e-2, wl=0.0 )

全连接层权重矩阵初始化并对其正则化

weight4 = variable_with_weight_loss( shape=[384,192], stddev=0.04, wl=0.004 )

2.2.7.5 LRN（Local Response Normalization）

LRN最早见于Alex那篇用CNN参加ImageNet比赛的论文，Alex在论文中解释了LRN层模仿了生物神经系统的“侧抑制”机制，对局部神经元的活动创建竞争环境，使得其中响应比较大的值变得相对更大，并抑制其他反馈较小的神经元，增强了模型的泛化能力。Alex在ImageNet数据集上的实验表明，使用LRN后CNN在Top1的错误率可以降低1.4%，因此在其经典的AlexNet中使用了LRN层，LRN对ReLU这种没有上限边界的激活函数会比较有用，因为它会从附近的多个卷积核的响应中挑选比较大的反馈，但不适合Sigmoid这种有固定边界并能抑制过大值得激活函数。

norm1 = tf.nn.lrn( input, 4, bias=1.0, alpha=0.001/9.0, beta = 0.75, name=name )

ImageNet中的LRN层是按下述公式计算的：

但在后来的神经网络设计中，LRN已经几乎不再被用到。

2.2.7.6 数据扩展

2.2.7.7 标准化处理

主要用到了tf.nn.moments函数和tf.nn.batch_normalization函数，相应定义分别如下：

def moments(x, axes, name=None, keep_dims=False)

参数意义如下：
• x 可以理解为我们输出的数据，形如 [batchsize, height, width, kernels]
• axes 表示在哪个维度上求解，是个list
• name 变量名
• keep_dims 是否保持维度
函数输出有两个
• mean 就是均值啦
• variance 就是方差啦
比较常用的有卷积神经网络中输入标准化：

def batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None):

参数意义如下：
• x 可以理解为我们输出的数据，形如 [batchsize, height, width, kernels]
• mean为上面求得的均值
• variance为上面求得的方差
• offset 均值的偏移量
• scale 标准化处理后再对输出值进行线性缩放的系数
• variance_epsilon 防止均方差趋于0，给均方差加上一个微小量
• name 操作名称

2.2.7.7.1 卷积层输入图像数据标准化

img = tf.Variable(tf.random_normal([32, 227, 227, 3])) 
axis = list(range(len(img.get_shape()) - 1)) 
mean, variance = tf.nn.moments(img, axis)
out = tf.nn.batch_normalization(x, mean, var, 0, 1, 1e-5)

上面代码的意思表示输入图像数据为32批3通道的227*227的矩阵，我们对每个通道的32组数据分别做标准化处理，求得的mean和variance的长度均是3（示意如下），然后再进行标准化处理。

2.2.7.7.2 加权输入标准化

当输入落入sigmoid函数或tanh函数的饱和区时会发生梯度消失现象，通过对加权输入进行标准化处理可以避免这一现象。标准化处理通过规范化使得加权输入的均值为0、方差为1，从而使得加权输入落入sigmoid函数的线性区间，避免了梯度消失，并可获得较大的梯度，从而加速收敛；梯度变大也使得模型更容易跳出局部最小值；此外，标准化处理还破坏了原来的数据分布，一定程度上缓解过拟合。下面给出了利用tensorflow实现对加权输入Wx_plus_b的标准化。

#利用tf.nn.moments(Wx_plus_b, axes=[0])计算Wx_plus_b的均值和方差，其中axes=[0]表示想要标准化的维度。
f_mean,f_var = tf.nn.moments(Wx_plus_b, axes=[0])
scale = tf.Variable(tf.ones([out_size]))#缩放比例
shift = tf.Variable(tf.zeros([out_size]))#平移项
eps = 0.001
Wx_plus_b = tf.nn.batch_normalization(Wx_plus_b, f_mean, f_var, shift, scale, eps)

等价于：

也可以通过sklearn.preprossing中的StandardScaler这个类来进行标准化，首先利用训练数据来算得标准化所需的平移值及方差，然后在利用transform进行变换：

Import sklearn.preprossing as prep
Preprocessor = prep.StandardScaler().fit(X_train)
X_train = Preprocessor.transform(X_train)
X_test = Preprocessor.transform(X_test)

2.2.8 模型的存储与加载

模型的存储及加载有助于我们训练网络时中途停顿以及继续训练，也有助于我们利用已经训练好的模型参数来训练自己的模型或进行应用。
(1)首先定义Saver对象：

saver = tf.train.Saver(max_to_keep=2)

max_to_keep用来设置保存模型的个数，可通过计数方式来决定保存与否。
(2)创建完Saver对象后就可以保存模型

saver.save(sess, checkpoint_dir + 'model.ckpt', global_step=i+1)  

第二个参数设定模型文件保存的路径和名字，第三个参数将训练的次数作为后缀加入到模型名字中，每次会生成

XXX.ckpt-ind.data-00000-of-00001
XXX.ckpt-ind.index
XXX.ckpt-ind.meta

这3个文件。然后global_step还可省略：

saver.save(sess, checkpoint_dir + 'model.ckpt')  

此时生成的ckpt文件名中没有迭代步数后缀：

XXX.ckpt.data-00000-of-00001
XXX.ckpt.index
XXX.ckpt.meta

文件名也可以任意设定：

saver.save(sess, './save_ckpt/%s_%s.ckpt' % (generator_name, style_name), global_step=i+1)

(3)记录下模型文件后，就可以加载模型文件

saver.restore (sess, tf.train.latest_checkpoint(checkpoint_dir))

checkpoint_dir为文件路径，通过tf.train.latest_checkpoint(checkpoint_dir)找出路径checkpoint_dir下最新的模型文件，并通过saver.restore加载到sess会话中。具体实例如下：

import tensorflow as tf  
import numpy as np  
isTrain = False 
isTrain = True 
train_steps = 1000  
checkpoint_steps = 50  
checkpoint_dir = './'  
x = tf.placeholder(tf.float32, shape=[None, 1])  
y = 5 * x + 5  
w = tf.Variable(tf.random_normal([1], -1, 1))  
b = tf.Variable(tf.zeros([1]))  
y_predict = w * x + b  
loss = tf.reduce_mean(tf.square(y - y_predict))  
train = tf.train.GradientDescentOptimizer(0.5).minimize(loss)  
saver = tf.train.Saver(max_to_keep=2)  # defaults to saving all variables - in this case w and b  
x_data = np.reshape(np.random.rand(10).astype(np.float32), (10, 1))  
with tf.Session() as sess:  
    sess.run(tf.global_variables_initializer())  
    if isTrain:  
        for i in range(train_steps):  
            loss_, _ = sess.run([loss, train], feed_dict={x: x_data})  
            if (i + 1) % checkpoint_steps == 0:  
                saver.save(sess, checkpoint_dir + 'model.ckpt', global_step=i+1)  
        print(sess.run(w))  
        print(sess.run(b)) 
    else:  
        model_file=tf.train.latest_checkpoint(checkpoint_dir)
        saver.restore(sess,model_file)
        print(sess.run(w))  
        print(b.eval())
        #sess.run()在同一步中获取多个tensor中的值，使用Tensor.eval()在同一步中获取一个tensor值。

2.3 定义损失函数和优化器

定义优化器前需选定损失函数

2.3.1 损失函数

损失函数用来描述模型前向输出的精度，损失函数输出值越小，表示模型的分类或回归结果与真实值偏差越小。

2.3.1.1 无正则化

y_ = tf.placeholder(tf.float32, [None, 10]) #输出变量占位符
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1])) #交叉熵损失函数

2.3.1.2 L2正则化

def lossFcn( logits, labels ):
    labels = tf.cast( labels, tf.int64 )
    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits( logits=logits, labels=labels, name='cross_entropy_per_example' )
    cross_entropy_mean = tf.reduce_mean( cross_entropy, name = 'cross_entropy' )
    tf.add_to_collection( 'losses', cross_entropy_mean )
return tf.add_n( tf.get_collection( 'losses' ), name = 'total_loss' )
loss = lossFcn( logits, label_holder )

2.3.1.3 交叉熵损失函数

对于多分类问题，常用交叉熵来定义损失函数：

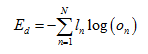
式中n为向量下标、N为向量维度、l为真实输出标签向量、o为输出向量。TensorFlow中的定义为：
cross_entropy = -tf.reduce_sum(l * tf.log(o), reduction_indices=1)
其中reduction_indices的取值与l及o的输出维度相关。如果使用MiniBatch来训练，损失函数可写为：

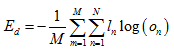
ensorFlow中的定义为：

cross_entropy = tf.reduce_mean(-tf.reduce_sum(l * tf.log(o), reduction_indices=[1]))

之所以这么用是因为对于随机小批量梯度下降法，l及o的维度为[batchsize, n_class]

2.3.1.4 tf.nn.softmax_cross_entropy_with_logits(logits, labels, name=None)

从字面意思可以看成，该损失函数为softmax与交叉熵损失函数的结合，其中参数logits为网络输出项，单样本的大小是n_class，按批训练的话样本大小为[batchsize, n_class]；参数labels为真实标签，维度同logits。该损失函数的具体计算流程为：先对输出logists做softmax处理，再利用第二个参数获取label表示的onehot向量，然后再计算交叉熵并返回交叉熵向量。由于该函数的返回值为交叉熵处理之后的输出向量之和，所以常常结合reduce_mean操作一同使用，以获得损失函数具体的值。

import tensorflow as tf
import numpy as np
sess = tf.Session();
logits_= np.array([[ 0.16623953, 0.14493713],[0.43981495,-0.13514614],[0.7059976, -0.40246272]])
labels_ = np.array([1,1,0])
sess.run(tf.global_variables_initializer())
a = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits_, labels=labels_)  
print('a:',sess.run(a))
c = tf.reduce_sum(-tf.multiply(tf.cast(tf.one_hot(labels_,2,1,0),tf.float64), tf.log(tf.nn.softmax(logits_))),1)
print('c:',sess.run(c))

下面来看tf.nn.sparse_softmax_cross_entropy_with_logits(_sentinel=None, labels=None, logits=None, name=None)
这个函数与上一个函数十分类似，唯一的区别在于labels。这个函数里要求labels的每一行为真实类别的索引。例如：

import tensorflow as tf
labels = [0,2]
logits = [[2,0.5,1], [0.1,1,3]]
result1 = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=labels, logits=logits)
with tf.Session() as sess:
    print sess.run(result1)
>>>[ 0.46436879  0.17425454]

2.3.2 定义优化器
TensorFlow技术解析与实战4.7节+http://blog.csdn.net/heyongluoyao8/article/details/52478715
(1)#设置学习速率为0.5，损失函数为cross_entropy

train_step = tf.train.GradientDescentOptimizer(0.3).minimize(cross_entropy) 

(2) #设置学习速率为0.3，损失函数为cross_entropy

train_step = tf.train.AdagradOptimizer(0.3).minimize(cross_entropy) 

(2) #设置学习速率为0.3，损失函数为loss

loss = lossFcn( logits, label_holder )
train_op = tf.train.AdamOptimizer( 1e-3 ).minimize( loss )

定义数据训练方式

2.4 训练模型和评估模型

2.4.1 全局参数初始化器

tf.global_variables_initializer().run()

2.4.2 训练模型

2.4.2.1 无放回的随机取得小批数据

Tensorflow实例中的MNIST数据集中已经定义好了随机获取无放回的小批数据的方法，但在自己定义的数据集中还需在定义一下，下面仿造了MNIST数据集中的next_batch函数给出了一种无放回的随机取得小批数据的函数定义。首先用fake_data判断是否生成虚假数据，如果不用虚假数据，由于上次读取的小批数据中的最后一个图片的位置为self._index_in_epoch-1，所以当前新小批数据的起始位置为self._index_in_epoch。新的起始位置+小批数据量batch_size得到新的小批数据结束位置self._index_in_epoch，如果self._index_in_epoch>所有数据个数self._num_examples，那么就进行新的一轮遍历，新的遍历开始之前，首先需从新生成用于数据读取的乱序，然后再读。

import numpy
def next_batch(self, batch_size, fake_data=False):
    if fake_data:
        fake_image = [1] * 784
        if self.one_hot:
            fake_label = [1] + [0] * 9
        else:
            fake_label = 0
        return [fake_image for _ in range(batch_size)], [fake_label for _ in range(batch_size)]
    start = self._index_in_epoch
    self._index_in_epoch += batch_size
    if self._index_in_epoch > self._num_examples: # epoch中的句子下标是否大于所有语料的个数，如果为True,开始新一轮的遍历
    # Finished epoch
        self._epochs_completed += 1
    # Shuffle the data
        perm = numpy.arange(self._num_examples) # arange函数用于创建等差数组
        numpy.random.shuffle(perm) # 打乱
        self._images = self._images[perm]
        self._labels = self._labels[perm]
        # Start next epoch
        start = 0
        self._index_in_epoch = batch_size
    assert batch_size <= self._num_examples
    end = self._index_in_epoch
    return self._images[start:end], self._labels[start:end]

2.4.2.2 采用小批量随机梯度下降法训练模型

for i in range(3000):                                 #迭代3000次
    batch_xs, batch_ys = mnist.train.next_batch(100)  #无放回的从训练数据中选取100条样本构成minibatch
#    train_step.run(feed_dict= {x: batch_xs, y_: batch_ys})       #喂（feed）给占位符(placeHolder)
    train_step.run(feed_dict= {x: batch_xs, y_: batch_ys, keep_prob: 0.75})

2.5 计算准确率

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))    #相同返回TRUE,否则返回FALSE，argmax中第2个参数1表示沿列这个维度比较大小（即比较每行数据的大小），从而返回每行中最大的数所在的位置
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))  #将bool值转换为float32, 计算准确率
print(accuracy.eval(feed_dict= {x: mnist.test.images, y_: mnist.test.labels}))