CS 188 | Introduction to Artificial Intelligence (1)

代理

    在人工智能中，目前的核心问题是创建一个理性的代理，它有一个目标，并试图执行一系列动作，为目标产生最佳预期结果。代理存在于一个环境中。作为一个非常简单的例子，西洋跳棋代理的环境是一个虚拟跳棋板，它与对手对决，棋子移动就是动作。环境和代理创造了一个世界。

    反射代理是一种不考虑其动作后果，而是基于当前的世界状况选择一种行为的反射代理。这些代理通常优于规划代理，它维护了一个世界模型，并使用这个模型来模拟执行各种动作。然后代理可以确定行为的假设结果，并可以选择最佳结果。这是模拟的“智慧”，即人类在试图确定最佳行动时所做的：在任何情况下做提前考虑。

状态 空间和搜索问题

    为了创建一个理性的规划代理，我们需要一种数学表达给定环境的方法,代理将存在于其中。要做到这一点，我们必须正式表达一个搜索问题:鉴于代理的当前状态（其在环境中的配置），如何才能达到满足其以最佳方式实现目标？

      制定这样一个问题需要四件事：

•状态空间-在给定世界中可能的所有状态的集合。

•后继函数-在一种状态和一种行动中承担并计算执行成本的函数 

•启动状态-代理最初存在的状态

•目标测试-将状态作为输入，并确定其是否为目标状态的函数。

      从根本上讲，搜索问题是先考虑开始状态，使用后继函数迭代计算各种状态的后继，直到达到目标状态，通过探索状态空间来解决的。在这一点上，我们将确定从开始状态到目标状态（通常称为计划）的路径。使用预先确定的策略确定状态被考虑的顺序，我们将涵盖类型策略和它们的实用性。

    在我们继续解决搜索问题之前，重要的是要注意世界状态和搜索状态的差异性。世界状态包含有关给定状态的所有信息，而搜索状态仅包含规划所需的世界信息（主要是为了提高空间利用率）。为了说明这些概念，我们将介绍本课程的Pacman示例。Pacman吃豆人的游戏很简单：吃豆人必须穿过迷宫，吃下所有（小）的食物颗粒，在迷宫里没有被恶毒的巡逻幽灵吃掉。如果吃了一个（大）能量弹丸，它在一段时间内为巡逻幽灵免疫，并获得点食幽灵的能力。

     让我们考虑一个游戏的变种，其中迷宫只包含吃豆人和食物颗粒。我们可以在这个场景中提出两个不同的搜索问题：

路径和吃所有点。试图解决的路径从迷宫中位置（x1，y1）到位置（x2，y2）的问题是最佳的，吃掉所有的点，试图在尽可能短的时间内解决迷宫中所有食物颗粒的消耗问题。

    下面列出了这两个问题的状态、操作、后续函数和目标测试：

• 路径

–状态：（X，Y）位置

-行动：北、南、东、西

–继任函数：仅更新位置

-目标测试：是否（x，y）=end？

•吃所有点

–状态：（X，Y）位置，点的布尔值

-行动：北、南、东、西

–继任函数：更新位置和布尔值

–目标测试：所有的点布尔值是否为False？

    注意，对于路径而言，其状态包含的信息比“吃所有点”的状态少，因为对于“吃所有点”的状态，我们必须保持与每个食物颗粒相对应的一系列布尔值，它是否被吃过。一个世界可能仍然包含更多的信息，如Pacman经过的总距离或者Pacman在当前位置（x，y）上访问的所有位置和点的布尔值。

状态空间大小

        在估计求解搜索的计算运行时经常出现的一个重要问题是状态空间的大小。这几乎完全是通过基本计数来完成的。其原理是如果给定世界中有n个变量对象，x1，x2，…，xn不同的值，则状态总数为x1·x2···Xn。

用Pacman来展示这个概念：

变量对象及其对应的可能性数如下：

•Pacman位置-Pacman可以位于120个不同的（X、Y）位置，并且只有一个Pacman

•Pacman方向-可以是北、南、东或西，总共有4种可能

•幽灵位置-有两个幽灵，每个幽灵可以位于12个不同的（x，y）位置

•食品颗粒配置-有30种食品颗粒，每种颗粒都可以食用或不食用。

根据基本计数原理，我们有120个Pacman位置，Pacman可以面向4个方向，12·12幽灵配置（每个幽灵12个），2·2·2·2=2^30个食品颗粒配置（每个在30个食物颗粒中，有两个可能的值——吃或不吃）。

这给了我们一个总的状态空间大小：

状态 空间 图和搜索树

    现在我们已经建立了状态空间的概念，将4个部分定义成1个。我们几乎准备好开始解决搜索问题，最后一个难题是状态空间、图表和搜索树。

    回想一下，图是由一组节点和一组连接不同节点对的边定义的。这些

边也可能有与其关联的权重。构造一个状态空间图，从一个状态到其后续状态之间存在有向边的节点。边代表动作，任何相关的权重代表执行相应操作的成本。通常，状态空间图太大，无法存储在内存中（即使上面的简单pacman示例也有≈10^13个可能的状态!!）但在解决问题的时候，最好在概念上记住它们。重要的是要注意在状态空间图中，每个状态都被精确地表示一次，根本不需要多次表示一个状态，这点在试图解释搜索时有很大帮助。

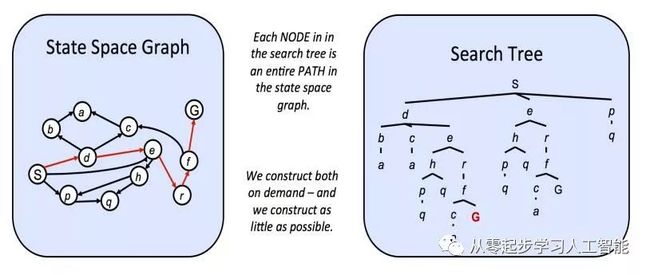
    与状态空间图不同，我们的下一个感兴趣的结构是搜索树，对一个状态可能出现的次数没有这样的限制。尽管搜索树也是一类以状态为节点的图，作为状态之间的边，每个状态/节点不仅对状态本身进行编码，而且 从开始状态到状态空间图中的给定状态对整个路径（计划）进行编码。  

     观察状态空间图对应的搜索树：

    给定状态空间图中突出显示的路径（s→d→e→r→f→g）表示为通过跟踪树中从开始状态s到突出显示的目标状态的路径来对应搜索树g。类似地，从开始节点到任何其他节点的每个路径在搜索树中都用从根到根的某个后代的路径，该后代对应于另一个节点。因为存在从一个状态到另一个状态的多种方法，状态往往在搜索树中出现多次。作为一个结果，搜索树的大小大于或等于其对应的状态空间图。我们已经确定了状态空间图本身的大小是巨大的，即使对于简单的问题。如果内存中数据很大我们如何对它们进行有用的计算呢？答案在于后继函数，我们只存储状态，使用相应的后续函数按需计算新的值。通常情况下，搜索问题是通过使用搜索树来解决的，存储一次要观察的选定节点，迭代地用它们的继承者替换节点，直到到达目标状态。

     各种各样的方法来决定执行搜索树节点迭代替换的顺序，如：

•  breadthFirstSearch  广度优先搜索

•  depthFirstSearch 深度优先搜索

•  aStarSearch 星际搜索算法

•  uniformCostSearch 一致代价搜索算法

欢迎关注微信公众号：“从零起步学习人工智能”。