tensorflow建立卷积神经网络

通过tensorflow来建立卷积神经网络。

要把一个算法彻底搞明白，需要明确以下几个概念1.算法的功能与适用条件2.算法的输入与输出分别是什么？3.算法的实现过程与组成部分。

ps: 此专题为AI领域经典算法书籍及论文解析与代码复现，AI算法讲解。欢迎关注知乎专栏《致敬图灵》
https://www.zhihu.com/people/li-zhi-hao-32-6/columns
微信公众号：‘致敬图灵’。

1.算法的功能：

对于图像的处理分类等应用具有很好的效果。

2.输入输出

首先是输入，在tensorflow中，需要将其定义为一个四维的张量，因为tensorflow中的conv2这个函数的输入规定输入为一个四维张量，我们可以通过如下语句进行定义：（x = tf.placeholder(“float”, shape = [None, 28,28,1])） ，这个四维张量的第一维是batch_size，也就是输入的样本的数量，第二维和第三维是图片的长和宽，第四维是颜色通道的数量。

而卷积运算的输出为可通过filter的定义来确定，W_conv1 = tf.Variable(tf.truncated_normal([5, 5, 1, 32], stddev=0.1))，最后生成的输出维32维的矩阵（这个矩阵是卷积运算后产生的）。

3.算法的组成部分

算法主要由三个部分组成。

3.1 filter

进行卷积操作的基本单元。

请见：https://www.cnblogs.com/hunttown/p/6830581.html。对卷积与池化进行了很好的解释。

3.2 非线性函数

进行filter卷积操作后，将每一个内积得到的值再进行传入非线性函数进行计算，如relu等。

3.3 池化层pool

如最大池化层，均值池化层等。

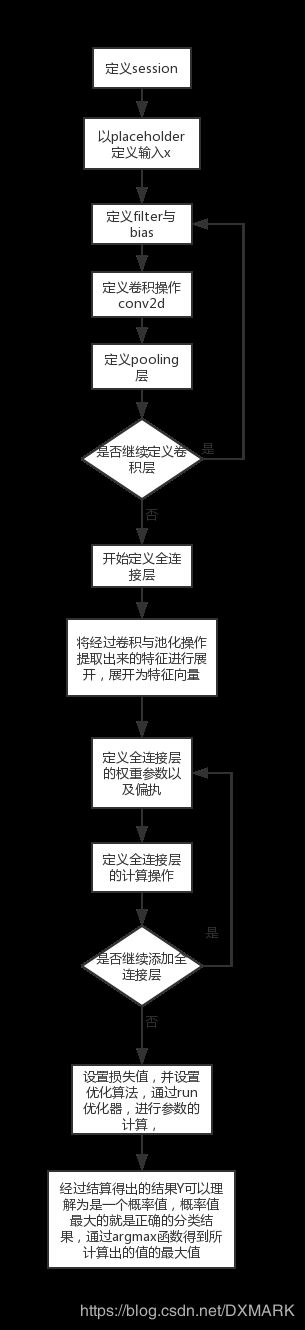
4.算法流程

import tensorflow as tf
import random
import numpy as np
import matplotlib.pyplot as plt
import datetime
%matplotlib inline

from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("data/", one_hot=True)

tf.reset_default_graph() 
sess = tf.InteractiveSession()
x = tf.placeholder("float", shape = [None, 28,28,1]) #shape in CNNs is always None x height x width x color channels 
#none 表示待定，根据具体传入的值进行改变。
y_ = tf.placeholder("float", shape = [None, 10]) #shape is always None x number of classes

W_conv1 = tf.Variable(tf.truncated_normal([5, 5, 1, 32], stddev=0.1))#shape is filter x filter x input channels x output channels 
#定义卷积中的filer，此filter的长宽为5*5，颜色通道数为1，输出的新特征为3D的，32层矩阵。
b_conv1 = tf.Variable(tf.constant(.1, shape = [32])) #shape of the bias just has to match output channels of the filter

h_conv1 = tf.nn.conv2d(input=x, filter=W_conv1, strides=[1, 1, 1, 1], padding='SAME') + b_conv1#进行卷积运算的函数
#此函数的参数，input，filter，strides，均为4维的，inputX每一维的含义由data_format决定，data_format默认格式为：[batchsize, height, width, channels]. batchsize为每一批的大小，一般设置批次为1，
#strides的第一个和最后一个参数规定一直取1，其第二和第三个参数表示每次进行滑动的步长，第二个表示横向滑动的步长，第三个表示纵向滑动的步长。


h_conv1 = tf.nn.relu(h_conv1) #
h_pool1 = tf.nn.max_pool(h_conv1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

def conv2d(x, W):
    return tf.nn.conv2d(input=x, filter=W, strides=[1, 1, 1, 1], padding='SAME')

def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

#Second Conv and Pool Layers
W_conv2 = tf.Variable(tf.truncated_normal([5, 5, 32, 64], stddev=0.1))
b_conv2 = tf.Variable(tf.constant(.1, shape = [64]))
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

#First Fully Connected Layer
W_fc1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1024], stddev=0.1))
b_fc1 = tf.Variable(tf.constant(.1, shape = [1024]))
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

#Dropout Layer
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

#Second Fully Connected Layer
W_fc2 = tf.Variable(tf.truncated_normal([1024, 10], stddev=0.1))
b_fc2 = tf.Variable(tf.constant(.1, shape = [10]))

#Final Layer
y = tf.matmul(h_fc1_drop, W_fc2) + b_fc2

crossEntropyLoss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels = y_, logits = y)) #p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量labels与logits的相似性
trainStep = tf.train.AdamOptimizer().minimize(crossEntropyLoss)
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

sess.run(tf.global_variables_initializer())

batchSize = 50
for i in range(1000):
    c = mnist.train.next_batch(batchSize)
    trainingInputs = batch[0].reshape([batchSize,28,28,1])
    trainingLabels = batch[1]
    if i%100 == 0:
        trainAccuracy = accuracy.eval(session=sess, feed_dict={x:trainingInputs, y_: trainingLabels, keep_prob: 1.0})
        print ("step %d, training accuracy %g"%(i, trainAccuracy))
    trainStep.run(session=sess, feed_dict={x: trainingInputs, y_: trainingLabels, keep_prob: 0.5})

step 0, training accuracy 0.14
step 100, training accuracy 0.94
step 200, training accuracy 0.96
step 300, training accuracy 0.98
step 400, training accuracy 0.96
step 500, training accuracy 1
step 600, training accuracy 0.98
step 700, training accuracy 0.98
step 800, training accuracy 1
step 900, training accuracy 0.98

可以看到结果还是不错的，进行100次迭代，准确率就已经可以达到0.9以上。

batchSize = 50
batch = mnist.train.next_batch(batchSize)
print(batch[0])
print(type(batch[0]))
print(batch[0].reshape([50,28,14,1,2,1,1,1,1,1,1]).shape) #通过reshape可以随意进行维度与形状的变换
print(batch[0].reshape([batchSize,28,14,2]))

​

​

​

​

​

​