网络流模板

网络流，顾名思义，是求网络中的流量。
这里的教程比较容易理解

主要性质：

• 容量限制 任何边的流量不能超过其流量。
• 斜对称 显然，若一条边的流量为w，即从u->v流量为w，可以看作是从v->u流量为-w。
• 流量守恒 网络中除原点，汇点以外，任何节点不储存流。这个也比较容易说明，因为如果某一时刻某个中间节点储存了流，则下一时刻它会储存更多。最后储存满了，这些满的流量不能流向汇点，就浪费了。

（lyd：网络流模型可以形象的描述为：在不超过流量限制的前提下，“流”从原点不断产生，流经整个网络，最终全部归于汇点。）

Edmonds-Karp算法

增广路：如果一条从起点到终点的路径上剩余流量都大于零，则最大流可以加上这条边流量的瓶颈，即这条路径上的最小剩余流量。EK的思想就是不断寻找增广路，直到找不到增广路为止。

具体实现：每次用BFS寻找增广路，若找到了，则将这条路径上的所有边减少增加的流量，还要把其反向边的流量增加相同的数值，重复上述过程，直到找不到增广路。

为什么要增加反向边的流量？因为算法不能保证每次找到的都是最优解。而构建反向边，则给了程序一个“反悔”的机会。在构建反向边后，如果另一条增广路需要经过已经寻找到增广路上的边，而这条边已经没有剩余流量了，就可以让原来的那条增广路走另一条路，这样又可以拓展出一条增广路。

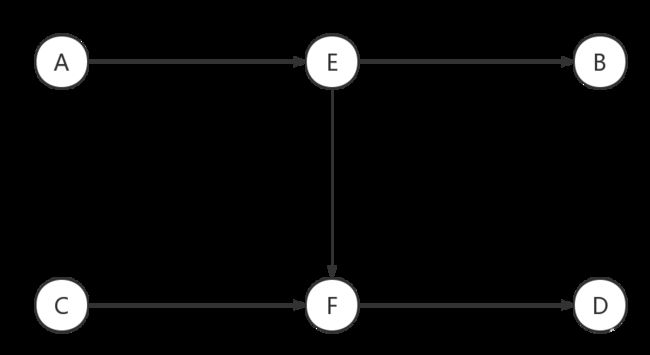
如图，若$A->E->F->D$是一条增广路，当寻找从$C$点的增广路时可以把$A$点的部分流量导到B点，即A的流量就变成了$A->E->F->D$和$A->E->B$两条。再拓展$C->F->D$这条路，就使得答案增加了。这一操作其实就等价于反向边上增加流量，因为反向边上增加多少，正向边就减少多少。

复杂度分析：由算法导论可得 算法复杂度是$O(n{m}^2)$。

模板题是luogu3376 【模板】网络最大流。

#include
#include
#include
#include
using namespace std;
const int MAXN = 10001;
const int MAXM = 100001;
const int INF = 0x3f3f3f3f;

int n, m, s, t, Ans;
int fir[MAXN], nxt[MAXM << 1], to[MAXM << 1], len[MAXM << 1], cnt;
int dis[MAXN], vis[MAXN], incf[MAXN], pre[MAXN];

inline int read(){
	int k = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){k = k*10 + ch - '0'; ch = getchar();}
	return k * f;
}

inline void add_edge(int a, int b, int l){
	len[cnt] = l;
	to[cnt] = b;
	nxt[cnt] = fir[a];
	fir[a] = cnt++; 
}

bool bfs(){
	queue <int> q; q.push(s);
	memset(vis, 0, sizeof(vis));
	vis[s] = 1; incf[s] = INF;
	while(!q.empty()){
		int u = q.front(); q.pop();
		for(int i = fir[u]; i != -1; i = nxt[i]){
			if(len[i]){
				int v = to[i];
				if(vis[v]) continue;
				incf[v] = min(incf[u], len[i]);
				pre[v] = i;
				q.push(v); vis[v] = true;
				if(v == t) return true;
			}
		}
	}
	return false;
}

void update(){
	int u = t;
	while(u != s){
		int i = pre[u]; //上一条边 
		len[i] -= incf[t];
		len[i^1] += incf[t];
		u = to[i^1];
	}
	Ans += incf[t];
}

void Edmonds_Karp(){
	while(bfs()) update();
}

int main(){
	memset(fir, -1, sizeof(fir));
	n = read(), m = read(), s = read(), t = read();
	for(int i = 1; i <= m; i++){
		int a = read(), b = read(), c = read();
		add_edge(a, b, c);
		add_edge(b, a, 0);
	}
	Edmonds_Karp();
	printf("%d", Ans);
	return 0;
}

Dinic算法

与Edmonds-Karp算法相似，都是寻找增广路径。只是Dinic通过dfs求出多条增广路，更为高效。通过构建分层图，DFS求出增广路，Dinic可以较高效地求出最大流。（233）具体原理可以戳这里

模板题同上。

#include
#include
#include
#include
using namespace std;
const int MAXN = 10001;
const int MAXM = 100001;
const int INF = 0x7fffffff;

int n, m, s, t;
int fir[MAXN], nxt[MAXM << 1], to[MAXM << 1], len[MAXM << 1], cnt;
int d[MAXN], Ans;

inline int read(){
	int k = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){k = k*10 + ch - '0'; ch = getchar();}
	return k * f;
}

inline void add_edge(int a, int b, int l){
	len[cnt] = l; to[cnt] = b; nxt[cnt] = fir[a]; fir[a] = cnt++;
	len[cnt] = 0; to[cnt] = a; nxt[cnt] = fir[b]; fir[b] = cnt++;
}

bool bfs(){
	queue <int> q;
	memset(d, 0, sizeof(d));
	d[s] = 1; q.push(s);
	while(!q.empty()){
		int u = q.front(); q.pop();
		for(int i = fir[u]; i != -1; i = nxt[i]){
			int v = to[i];
			if(len[i] && !d[v]){
				d[v] = d[u] + 1;
				q.push(v);
				if(v == t) return true;
			}
		}
	}
	return false;
}

int dfs(int u, int flow){
	if(u == t) return flow;
	int ret = flow;
	for(int i = fir[u]; i != -1; i = nxt[i]){
		int v = to[i];
		if(len[i] && d[v] == d[u] + 1){
			int k = dfs(v, min(ret, len[i]));
			if(!k) d[v] = 0;
			len[i] -= k;
			len[i^1] += k;
			ret -= k;
		}
	}
	return flow - ret;
}

void Dinic(){
	int flow = 0;
	while(bfs()){
		while(flow = dfs(s, INF)) Ans += flow;
	}
}

int main(){
	memset(fir, -1, sizeof(fir));
	n = read(), m = read(), s = read(), t = read();
	for(int i = 1; i <= m; i++){
		int a = read(), b = read(), l = read();
		add_edge(a, b, l);
	}
	
	Dinic();
	
	printf("%d", Ans);
	return 0;
}