回溯法和八皇后问题

一、回溯法

回溯法（探索与回溯法）是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。

二、八皇后问题

（一）问题描述

在国际象棋中，皇后是最强大的一枚棋子，可以吃掉与其在同一行、列和斜线的敌方棋子。比中国象棋里的车强几百倍，比她那没用的老公更是强的飞起（国王只能前后左右斜线走一格）。
八皇后问题是这样一个问题：将八个皇后摆在一张8*8的国际象棋棋盘上，使每个皇后都无法吃掉别的皇后，一共有多少种摆法？
八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。计算机发明后，有多种计算机语言可以解决此问题。

（二）分析过程

为了使问题简化，假定国王与四位皇后离了婚，那么只剩下四位皇后了。八皇后问题就变成了四皇后问题。

 

 

在第一行放1号皇后。第一行的四个格子都可以放。按枚举的习惯，先放在第一个格子。如下图所示。黑色的格子不能放其他的皇后。

 

在第二行放2号皇后，只能放在第三个或第四个格子。按枚举的习惯，先放在第三个格子，如下图所示。

 

 

不好了，前两位皇后沆瀣一气，已经把第三行全部锁死了，第三位皇后无论放哪里都难逃被吃掉的厄运。于是在第一个皇后位于1号，第二个皇后位于3号的情况下问题无解。我们只能返回上一步来，给2号皇后换个位置，挪到第四个格子上。

 

 

显然，第三个皇后只有一个位置可选。当第三个皇后占据第三行蓝色空位时，第四行皇后无路可走，于是发生错误，返回上层挪动3号皇后，而3号也别无可去，继续返回上层挪动2号皇后，2号已然无路可去，继续返回上层挪动1号皇后。于是1号皇后改变位置如下，继续搜索。

 

 

分析到这里，想必小朋友们对“回溯法”已经有了基本概念。下面要将算法实现出来。

（三）代码实现

1 queen()函数

void queen(int row) { if(row == n) { // 从0到n-1行，全部都已经放上皇后了，所以答案+1 total++; // 打印出n个皇后具体放在0~n-1行的第几列 for(int i = 0; icout << c[i] << " "; } cout << endl; } else { for(int col = 0; col != n; col++) { c[row] = col; if(check(row)) { queen(row + 1); } } } } 

算法是逐行安排皇后的，其参数row为现在正执行到第几行。n是皇后数，在八皇后问题里当然就是8啦。
if(row == n)这句代码好理解，如果程序执行了row == n，说明从0到n-1的位置都放上了皇后，那自然是找到了一种解法，于是八皇后问题解法数加1。
否则进入else语句。遍历所有列col，将当前col存储在数组c里，然后使用check()检查row行col列能不能摆皇后，若能摆皇后，则递归调用queen去安排下一列摆皇后的问题。

还不太清楚？再慢点来，刚开始的时候row = 0，意思是要对第0行摆皇后了。
If判断失败，进入else，进入for循环，col初始化为0
显然，0行0列的位置一定可以摆皇后的，因为这是第一个皇后啊，后宫空荡她想怎么折腾就怎么折腾，于是check(0)测试成功，递归调用queen(1)安排第1行的皇后问题。

皇后放在第1行时即row=1，进来if依然测试失败，进入for循环，col初始化为0。1行0列显然是不能摆皇后的，因为0行0列已经有一个圣母皇太后在那搁着了，于是check()测试失败，循环什么也不做空转一圈，col变为1。1行1列依然check()测试失败，一直到1行2列，发现可以摆皇后，于是继续递归queen(2)去安排第二个皇后位置。

如果在某种情况下问题无解呢？例如前面在4皇后问题中，0行0列摆皇后是无解的。假设前面递归到queen(2)时候，发现第2行没有地方可以摆皇后，那怎么办呢？要注意queen(2)的调用是在queen(1)的for循环框架内的，queen(2)若无解，则自然而然queen(1)的for循环col自加1，即将第1行的皇后从1行2列改为1行3列的位置，检查可否放皇后后继续安排下一行的皇后。如此递归，当queen(0)的col自加到n-1，说明第一列的皇后已经遍历了从0行1列到0行n-1列，此时for循环结束，程序退出。

在主函数中调用queen(0)，得到正确结果，8皇后问题一共有92种解法。

2 check函数

bool check(int curRow) { //放当前行的皇后时，只需要检查跟前面那些行的皇后有没有冲突 //不需要考虑后几行，因为后几行的皇后还没放上去呢 for(int preRow = 0; preRow != curRow; preRow++) { if(c[curRow] == c[preRow] || curRow - c[curRow] == preRow - c[preRow] || curRow + c[curRow] == preRow + c[preRow]) { return false; } } return true; } 

这里curRow表示当前的行。假定当前的行为第3行（从0开始计数）。那么for循环里，preRow = 0表示第0行，preRow = 1表示第1行，preRow = 2表示第2行。
c[curRow]表示第curRow行所在的列。比如c[3] = 2表示第三行第2列。c[0] = 2表示第0行第2列等。

(1) c[curRow] == c[preRow]

表示第row行和第preRow行的列一样，这样两个皇后就冲突了，所以返回false。

(2) curRow - c[curRow] == preRow - c[preRow]

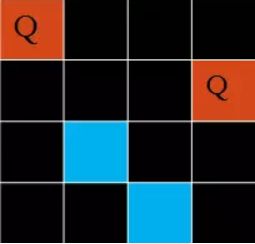
表示curRow行c[curRow]列与preRow 行c[preRow]列，在同一条斜率为负的斜线上。这样两个皇后也冲突了。以下图为例

 

 

例1

A格子，preRow = 0, c[preRow] = c[0] = 0，即第0行第0列。C格子，curRow = 2, c[curRow] = c[2] = 2, 即第2行第2列。curRow - c[curRow] == preRow - c[preRow]，表示这两个格子在一条斜线上，返回false。

例2

B格子，preRow = 1, c[preRow] = c[1] = 0，即第1行第0列。D格子，curRow= 3, c[curRow] = c[3] = 2, 即第3行第2列。curRow - c[curRow] == preRow - c[preRow]，表示这两个格子在一条斜线上，返回false。

(3) curRow + c[curRow] == preRow + c[preRow]

表示curRow行c[curRow]列与preRow行c[preRow]列，在同一条斜率为正的斜线上。这样两个皇后也冲突了。如下图所示：

 

 

例3

A格子，preRow = 0, c[preRow] = c[0] = 1，即第0行第1列。B格子，curRow = 1, c[curRow] = c[1] = 0, 即第1行第0列。curRow + c[curRow] == preRow + c[preRow]，表示这两个格子在一条斜线上，返回false。

例4

C格子，preRow = 0, c[preRow] = c[0] = 3，即第0行第3列。D格子，curRow= 3, c[curRow] = c[3] = 0, 即第3行第0列。curRow+ c[curRow] == preRow + c[preRow]，表示这两个格子在一条斜线上，返回false。

注意：上面表示两种斜线的情况，一种用的是“-”，另一种用的是“+”，其实是因为这两种线的斜率分别为-1和1的缘故。

3 完整代码

#include
#include using namespace std; int n = 8; int total = 0; int *c = new int(n); //也可以写为int c[n];表示皇后放在第几列 bool check(int curRow) { //放当前行的皇后时，只需要检查跟前面那些行的皇后有没有冲突 //不需要考虑后几行，因为后几行的皇后还没放上去呢 for(int preRow = 0; preRow != curRow; preRow++) { if(c[curRow] == c[preRow] || curRow - c[curRow] == preRow - c[preRow] || curRow + c[curRow] == preRow + c[preRow]) { return false; } } return true; } void queen(int row) { if(row == n) { // 从0到n-1行，全部都已经放上皇后了，所以答案+1 total++; // 打印出n个皇后具体放在0~n-1行的第几列 for(int i = 0; icout << c[i] << " "; } cout << endl; } else { for(int col = 0; col != n; col++) { c[row] = col; if(check(row)) { queen(row + 1); } } } } int main() { queen(0); cout << total << endl; return 0; } 

运行结果：

……
6 2 0 5 7 4 1 3
6 2 7 1 4 0 5 3
6 3 1 4 7 0 2 5
6 3 1 7 5 0 2 4
6 4 2 0 5 7 1 3
7 1 3 0 6 4 2 5
7 1 4 2 0 6 3 5
7 2 0 5 1 4 6 3
7 3 0 2 5 1 6 4
92

三、回溯法和枚举法的区别

回溯法与穷举法有某些联系，它们都是基于试探的。
穷举法要将一个解的各个部分全部生成后，才检查是否满足条件，若不满足，则直接放弃该完整解，然后再尝试另一个可能的完整解，它并没有沿着一个可能的完整解的各个部分逐步回退生成解的过程。
而对于回溯法，一个解的各个部分是逐步生成的，当发现当前生成的某部分不满足约束条件时，就放弃该步所做的工作，退到上一步进行新的尝试，而不是放弃整个解重来。