Gabor滤波器为什么能实现频率域加窗
Gabor 特征是一种可以用来描述图像纹理信息的特征,Gabor 滤波器的频率和方向与人类的视觉系统类似,特别适合于纹理表示与判别。
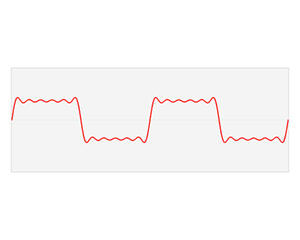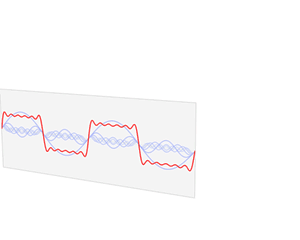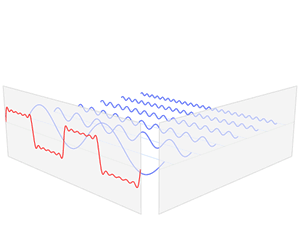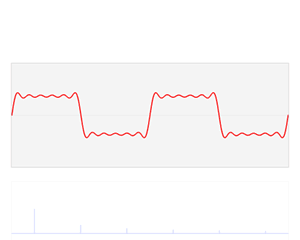
Gabor 特征主要依靠 Gabor 核在频率域上对信号进行加窗,从而能描述信号的局部频率信息。
说到 Gabor 核,不能不提到傅里叶变换。正是靠傅里叶变换,我们才能将信号转换到频率域,才能让Gabor核在频率域去加窗。而在原本的空间域中,一个 Gabor 核实际上就是一个高斯核与正弦波调制的结果,可以看做是高斯核应用在了正弦波的频域部分。
上面说的还是比较笼统,下面我们一步一步介绍Gabor核是怎么对信号“加窗”的。
一、傅里叶变换
关于傅里叶变换,韩昊同学总结过一个很直观的解释。我这里就不赘述了。
总之,傅里叶变换是图像处理里面一个很重要的工具,本质是将任意一个函数转化为若干不同频率正弦波的组合,(组合方式在离散函数中就是相加,在连续函数中就是积分)。由此,将空域(或时域)信号转换到了频域(即频率域)。
空间域中多个波叠加,在频率域中就对应着若干个散落的点。韩昊同学将其比喻为不同音阶组成的音谱。
频率域中的基本元素就是正弦波:空间域中的一个正弦波波形,在频率域中只要一个点就能表示。
维基百科上有一个动态图,展示了一个叠加波如何分解到频率域上的若干点:
事实上,任何波都可以看做是若干(乃至无穷)个不同频率正弦波的叠加。
就像可见光可以看做不同频率的光的叠加一样,通过傅里叶变换,我们能将任何波分解为不同频率波的叠加。这样转换的好处是:有些情况下空域中很复杂的问题,在频率域会变得十分简单。
二、Gabor 核
2.1 一维 Gabor 核
2.1.1 一维傅里叶变换
一维傅里叶变化定义如下:
其中,f 为输入信号, ξ ξ 表示分解得到的各个波的频率, f^(f,ξ) f^(f,ξ) 为变换后的信号。公式中的 e−i2πxξ e−i2πxξ 表示一个复数波,关于复数波的解释可以看我之前的一篇文章
从上面的公式可以看出,原信号 f(t) f(t) 以 t 为自变量,描述了信号值随时间的变化,说明原信号空间在时间域中。经过傅里叶变换后,函数自变量变为了 ξ ξ , f^(ξ) f^(ξ) 描述了信号值随频率的变化,即信号转换到了频率域空间中。如果说原来信号的图示需要以时间(空间)为坐标轴的话,信号在傅里叶变换后的图示就需要以频率为坐标轴了。
2.1.2 一维 Gabor 核
一维Gabor核由一个高斯核与一个复数波的乘积定义:
其中,
这里, f0 f0 是复数波 s(t) s(t)的频率。
将复数波 s(t)=ei(2πf0t) s(t)=ei(2πf0t)代入 2 2式中,得到:
上面最后一步得到了 Gabor 核的复数表示,我们就可以按实部和虚部将其拆分为实核和虚核,在很多应用中,我们只需要应用 Gabor核的实数部分即可:
2.1.3 Gabor 核的傅里叶变换
将 Gabor 核(式 2 2)套入一维傅里叶变换(式 1 1)中,得到 Gabor 核的傅里叶变换:
上式中出现了 ω^(f−f0a) ω^(f−f0a) 的形式,这里需要补充高斯核一个很有趣的性质: ω^(f)=ω(f)=e−πf2 ω^(f)=ω(f)=e−πf2,这个性质这里就不证明了,有兴趣的同学可以自己推导一下。根据这个性质,上式中的 ω^(f−f0a) ω^(f−f0a) 也可以写作 ω(f−f0a) ω(f−f0a),二者可以自由转换。
此外, 3 3式中的末尾,我们知道了Gabor核傅里叶变换后是这样一个形式: kaeiθω^(f−f0a) kaeiθω^(f−f0a),这个形式可以看做是一个复数波,它的幅度
也就是说,Gabor核相当于在频率域应用了一个高斯核窗口。假设我们这时有了一个信号的频率域: fin(f) fin(f),那么我们直接用频率域的Gabor核 Gabor^ Gabor^ 与其相乘,就实现了对 f0 f0 频率邻域范围内的滤波效果:输入信号频率离这个 Gabor 核的 f0 f0 越远,则乘上Gabor核之后的结果就越小,尤其是当 fin fin 在 f0 f0 的 3σ 3σ 区间外时,这个频率几乎可以忽略不计。于是,最终能保留下来的信号就都是 f0 f0 频率附近的信号了。
这个想法,用公式表示出来就是:
从这个角度出发,给我们任意一个输入信号,我们先用傅里叶变换将其变换到频率域得到 fin^ fin^,再用 Gabor 核的傅里叶变换结果与之相乘,就是频域滤波的结果了。
不过我们大可不必这么麻烦,因为有卷积定理:
这样看来,我们只需要用 Gabor 核和输入信号卷积就可以得到输入信号在某频率邻域附近的响应结果!!
我们既可以用这个响应结果来实现频域滤波,又可以用它来描述信号的频率信息。下面要提到的Gabor特征,就是用Gabor核来描述信号的频率信息,从而作为信号的特征的。
2.2 二维 Gabor 变换
将上面的一维情况推广至二维:
2.2.1 二维傅里叶变换:
二维傅里叶变换定义如下:
为了简洁,改用 (u0,v0) (u0,v0) 来代替 (ξx,ξy) (ξx,ξy),则上式可写为:
提醒一下,这里 (x,y) (x,y) 表示空域坐标, (u0,v0) (u0,v0) 表示频域坐标。
2.2.2 二维复数波
二维复数波完整定义如下(用复指数形式表示):
由于初始相位对Gabor核影响不大,因此可以将其省略,得到更简洁的形式(论文中关于 Gabor 函数的定义各不一样,主要是这些细节的考虑不同):
2.2.3 二维高斯函数
二维高斯函数定义如下:
其中, σx,σy σx,σy 分别为两个方向上的尺度参数(scaling parameters),用来控制高斯函数在两个方向上的“展布”形状。 (x0,y0) (x0,y0) 为高斯函数的中心点。 K K 为常数。
考虑全面的话,高斯函数还要有(顺时针)旋转,即:
加入旋转参数后的二维高斯函数为:
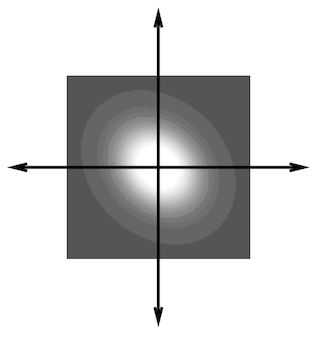
二维高斯
上图即是一个二维高斯核的图像,该高斯核中, (x0,y0)=(0,0) (x0,y0)=(0,0), (σ2x,σ2y)=(50,40) (σx2,σy2)=(50,40), θ=−45° θ=−45°
从图像可以看出, σx和σy σx和σy分别控制了高斯两个方向的“展布”情况。
2.2.4 Gabor 滤波器核
类似一维 Gabor 核,我们将二维高斯函数与二维复数波相乘,就得到了二维的Gabor核:
它的各个参数含义如下:
- (x0,y0) (x0,y0): 高斯核的中心点
- θ θ: 高斯核的旋转方向(顺时针)
- (σx,σy) (σx,σy): 高斯核两个方向上的尺度
- (u0,v0) (u0,v0): 频域坐标
- K K: 高斯核的幅度(magnitude)的比例
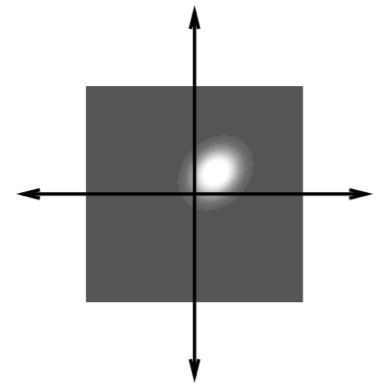
Gabor 核频率域图示
上图为Gabor核在频率域中的图示,这个Gabor核就是从之前那个高斯核得到的,其参数分别为: u0=v0=1/80 u0=v0=1/80, x0=y0=0 x0=y0=0, σ2x=50 σx2=50, σ2y=40 σy2=40, θ=−45° θ=−45°, F0=2–√/80 F0=2/80, ω0=45° ω0=45°。
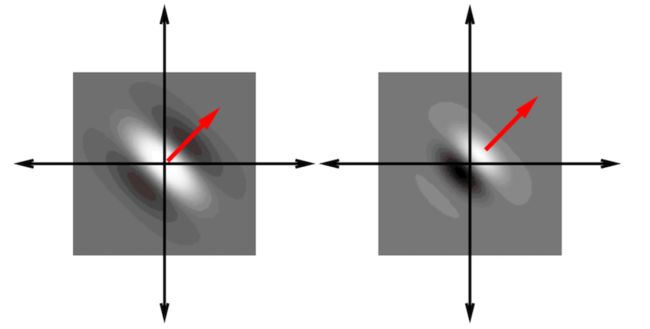
Gabor 核空间域图示
上图为Gabor核在空间域中的图示,参数和上面那个Gabor核一样。图像左边是实部,右边是虚部。这样的Gabor核与图像进行卷积,我们便能得到图像在 (u0,v0) (u0,v0)频率附近的响应情况。在图像处理中,通常使用Gabor的实部进行卷积就可以。
三、Gabor 核作为图像特征
通过上面的分析,我们知道了,一个Gabor核能获取到图像某个频率邻域的响应情况,这个响应结果可以看做是图像的一个特征。那么,我们如果用多个不同频率的Gabor核去获取图像在不同频率邻域的响应情况,最后就能形成图像在各个频率段的特征,这个特征就可以描述图像的频率信息了

一系列 Gabor 核
上图展示了一系列具有不同频率的 Gabor 核,用这些核与图像卷积,我们就能得到图像上每个点和其附近区域的频率分布情况。
由于纹理特征通常和频率相关,因此Gabor核经常用来作为纹理特征。又因为字符识别问题通常都是识别纹理的过程,所以Gabor核在光学字符识别(OCR)系统中也有广泛应用。
写在最后
由于本人对信号处理不是太了解,因此对傅里叶变换、频率域的理解都是个人粗浅的理解。为了完成这篇文章,我学习了很多信号处理的知识,重新理解了一些基本概念,看别人的帖子建立过一些认识,随后这层理解不牢又被推翻,再重新建立……前前后后用了一周的时间才最终完成。如有不严谨或错误的地方,还请大家谅解。要严肃学习的话最好还是看权威教材、看论文,我这篇文章可以作为另一个角度的补充。
参考资料
- 中文维基百科 / 傅里叶变换
- 韩昊同学对傅里叶变换的直观解释
- 中文维基百科 / 卷积定理
- 英文维基百科 / Gabor_filter
- 英文维基百科 / Gabor_transform
- Movellan J R. Tutorial on Gabor filters[J]. Open Source Document, 2002.
- Idrissa M, Acheroy M. Texture classification using Gabor filters[J]. Pattern Recognition Letters, 2002, 23(9): 1095-1102.
版权声明
本文所有文字版权均属本人所有,如需转载请注明来源。