计算机视觉(九):特征描述(feature description)
- 一、 特征描述子(descriptor)
- 二、表示
- 1. 边界追踪
- 2. 链码
- 三、边界描述子
- 1. 一些简单描述子
- 2. 形状数
- 3. 傅里叶描述子
- 4. 统计矩
- 四、区域描述子
- 1. 一些简单的描述子
- 2. 拓扑描述子
- 3. 纹理
- 五、SIFT(未完,待续)
一、 特征描述子(descriptor)
分割后的像素集经常以一种适合于计算机进一步处理的形式来表示和描述。基本上,表示一个区域涉及两种选择:
① 根据其外部特征(其边界)来表示区域
② 根据其内部特征(如组成该区域的像素)表示区域
下一项任务是基于所选择的表示来描述区域。当我们关注的重点是形状特征时,可选择一种外部表示;而当关注的重点是内部属性如颜色和纹理时,可以选择一种内部表示。有时,需要同时使用这两种表示。无论哪种情形,选择用来作为描述子的特征都应尽可能地对大小、平移和旋转不敏感。
二、表示
前面讨论的图像分割技术以沿着边界或包含在区域中的像素的形式产生原始数据。标准做法是使用某种方案将分割后的数据精简为便于描述子计算的表示。以下讨论各种表示方法。
1. 边界追踪
边界追踪算法的输出是排过序的点的序列。给定一个二值区域R或其边界,追踪R的边界或给定边界的算法如下:
① 令起始点 b 0 b_0 b0 为图像中左上角标记为1的点。使用 c 0 c_0 c0 表示 b 0 b_0 b0 西侧的邻点。很明显, c 0 c_0 c0 总是背景点。从 c 0 c_0 c0 开始按顺时针方向考察 b 0 b_0 b0 的8个邻点。令 b 1 b_1 b1 表示所遇到的值为1的第一个邻点,并直接令 c 1 c_1 c1(背景)是序列中 b 1 b_1 b1 之前的点。存储 b 0 b_0 b0 和 b 1 b_1 b1 的位置,以便在步骤5中使用。
② 令 b = b 1 b=b_1 b=b1 和 c = c 1 c=c_1 c=c1
③ 从 c c c 开始按顺时针方向行进,令 b b b 的8个邻点为 n 1 , n 2 , . . . , n 8 n_1,n_2,...,n_8 n1,n2,...,n8。找到标为1的第一个 n k n_k nk。
④ 令 b = n k b=n_k b=nk 和 c = n k − 1 c=n_k-1 c=nk−1
⑤ 重复步骤3和步骤4,直到 b = b 0 b=b_0 b=b0 且找到的下一个边界点为 b 1 b_1 b1。
算法停止时,所找到的 b b b 点的序列就构成了排列后的边界点的集合。
2. 链码
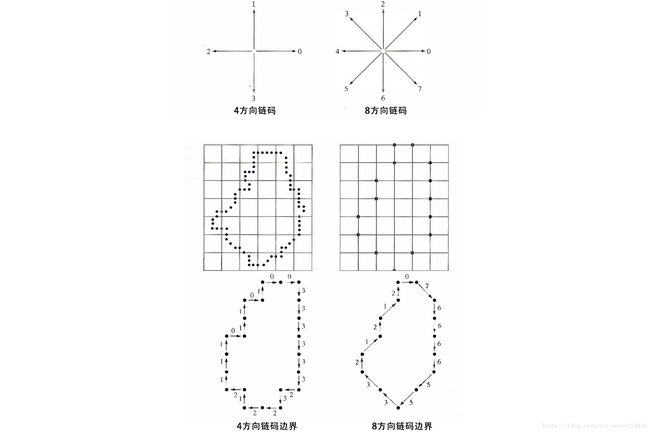
链码用于表示由顺次连接的具有指定长度和方向的直线段组成的边界。这种表示基于这些线段的4连接或8连接。每个线段的方向使用一种数字编号方案编码,如图1所示,以这种方向性数字序列表示的编码称为佛雷曼(Freeman)链码。
链码的一次差分为,通过计算链码中分隔两个相邻像素的方向变化的数(按逆时针方向计算前一个数字变化到后一个数字所需的步数),其中第一元素是通过使用链码的最后一个元素和第一个元素间的转变来计算得到的。例如,4方向链码0231,得到的一次差分为3212,其中3为1逆时针转到0需3步;2为0逆时针转到2需2步;1为2逆时针转到3需1步;2为3逆时针转到1需2步。
若旋转图像,链码会发生改变。而链码的一次差分则不受旋转影响。
三、边界描述子
1. 一些简单描述子
① 边界的长度
边界的长度是其最简单的描述子之一。一条边界上的像素数量可以给出其长度的粗略近似。
② 边界的长轴与短轴
边界B的直径定义为
D i a m ( B ) = max i , j [ D ( p i , p j ) ] Diam(B) = \max_{i, j}\ [D(p_i, p_j)] Diam(B)=i,jmax [D(pi,pj)]式中, p i , p j p_i, p_j pi,pj 是边界上的点, D ( p i , p j ) D(p_i, p_j) D(pi,pj) 是定义 p i p_i pi 和 p j p_j pj 之间的距离。直径的值和连接组成该直径的两个端点的直线段(该直线称为边界的长轴)的方向是边界的有用描述子。边界的短轴定义为与长轴垂直的直线,且由边界与两个轴相交的4个外部点所组成的方框(该方框称为基本矩形),可以完全包围该边界。
③ 边界的偏向率
长轴与短轴之比称为边界的偏心率。
2. 形状数
链码边界的一次差分取决于起始点。一条基于链码的边界的形状数,定义为最小量级的一次差分,即对链码的一次差分进行循环,得到的值最小的差分码为形状数。
3. 傅里叶描述子
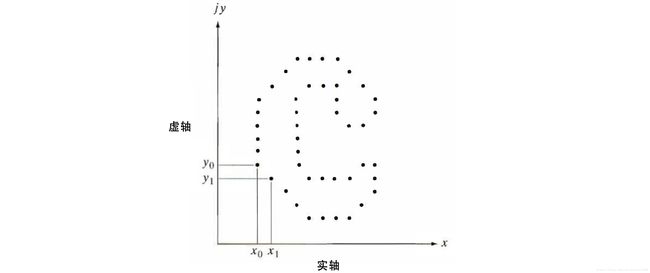
图2显示了 x y xy xy 平面内的一个 K K K 点数字边界。从任意点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0) 开始,以逆时针方向在该边界上行进时,会遇到坐标对 ( x 0 , y 0 ) , ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x K − 1 , y K − 1 ) (x_0,y_0),(x_1,y_1),(x_2,y_2),...,(x_{K-1},y_{K-1}) (x0,y0),(x1,y1),(x2,y2),...,(xK−1,yK−1)。这些坐标可以表示为 x ( k ) = x k x(k) = x_k x(k)=xk, y ( k ) = y k y(k) = y_k y(k)=yk 的形式,此外,每个坐标对可当作一个复数来处理,即
s ( k ) = x ( k ) + j y ( k ) s(k) = x(k) + jy(k) s(k)=x(k)+jy(k)式中 k = 0 , 1 , 2 , . . . , K − 1 k=0,1,2,...,K-1 k=0,1,2,...,K−1。
s ( k ) s(k) s(k) 的傅里叶变换为
a ( u ) = ∑ k = 0 K − 1 s ( k ) e − j 2 π u k / K a(u) = \sum_{k=0}^{K-1}s(k)e^{-j2\pi uk / K} a(u)=k=0∑K−1s(k)e−j2πuk/K式中 u = 0 , 1 , 2 , . . . , K − 1 u=0,1,2,...,K-1 u=0,1,2,...,K−1。复系数 a ( u ) a(u) a(u) 称为边界的傅里叶描述子。这些系数的傅里叶反变换可恢复 s ( k ) s(k) s(k)。也就是说,
s ( k ) = 1 K ∑ u = 0 K − 1 a ( u ) e j 2 π u k / K s(k) = {1\over K}\sum_{u=0}^{K-1}a(u)e^{j2\pi uk / K} s(k)=K1u=0∑K−1a(u)ej2πuk/K然而,假设仅使用前 P P P 个傅里叶系数而不使用所有系数,等同于在上式中令 a ( u ) = 0 , u > P − 1 a(u)=0, u>P-1 a(u)=0,u>P−1。结果为 s ( k ) s(k) s(k) 的如下近似:
s ^ ( k ) = 1 K ∑ u = 0 P − 1 a ( u ) e j 2 π u k / P \hat s(k) = {1\over K}\sum_{u=0}^{P-1}a(u)e^{j2\pi uk / P} s^(k)=K1u=0∑P−1a(u)ej2πuk/P尽管求 s ^ ( k ) \hat s(k) s^(k) 的每个成分时仅使用了 P P P 项,但 k k k 的范围仍是从 0 0 0 到 K − 1 K-1 K−1。也就是说,在近似边界中存在同样数量的点,但项数不像在每个点的重建中那么多。
由于高频成分说明精细细节,而低频成分决定全局形状,因此, P P P 越小,边界丢失的细节就越多。
4. 统计矩
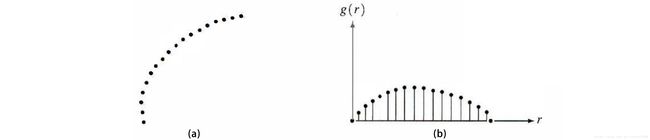
考虑图3(a),它显示了一段边界,而图3(b)显示了以任意变量 r r r 的一维函数 g ( r ) g(r) g(r) 描述的线段。该函数是这样获得的:先将该线段的两个端点连接,然后旋转该直线线段,直至其为水平线段。此时,所有点的坐标也旋转同样的角度。
将 g ( r ) g(r) g(r) 归一化为单位面积,并把它当作直方图来处理。换句话说, g ( r i ) g(r_i) g(ri) 现在作为值 r i r_i ri 出现的概率来处理。此时, r r r 为一个随机变量,故n阶矩为
u n ( r ) = ∑ i = 0 K − 1 ( r i − m ) n g ( r i ) u_n(r) = \sum_{i=0}^{K-1}(r_i-m)^ng(r_i) un(r)=i=0∑K−1(ri−m)ng(ri)
式中,
m = ∑ i = 0 K − 1 r i g ( r i ) m = \sum_{i=0}^{K-1}r_ig(r_i) m=i=0∑K−1rig(ri)式中, K K K 是边界上的点数, u n ( r ) u_n(r) un(r) 直接与 g ( r ) g(r) g(r) 的形状相关。例如,二阶矩 u 2 ( r ) u_2(r) u2(r) 度量曲线关于 r r r 的均值的扩展程度,而三阶矩 u 3 ( r ) u_3(r) u3(r) 度量曲线关于均值的对称性。
四、区域描述子
1. 一些简单的描述子
① 区域的面积
区域的面积定义为该区域中像素的数量。
② 区域的周长
区域的周长是其边界的长度。
③ 致密性
致密性定义为(周长)2/面积。
④ 圆度率
圆度率即一个区域的面积与具有相同周长的一个圆(最致密形状)的面积之比。周长为 P P P 的一个圆的面积为 P 2 / 4 π P^2/4\pi P2/4π。因此,圆度率 R c R_c Rc 由下式给出:
R c = 4 π A P 2 R_c = {4\pi A\over P^2} Rc=P24πA式中, A A A 是所讨论区域的面积, P P P 是其周长。
⑤ 其他
用做区域描述子的其他简单测度包括灰度级的均值和中值、最小灰度值和最大灰度值,以及其值高于和低于均值的像素数。
2. 拓扑描述子
拓扑学研究未受任何变形影响的图形的特质,前提是该图形未被撕裂或粘连。
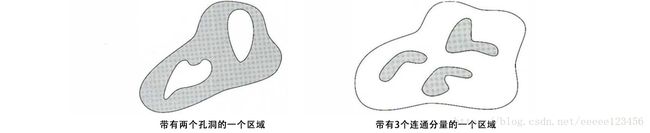
例如,图4(a)显示了一个带有两个孔洞的区域。如果一个拓扑描述子由该区域内的孔洞数量来定义,那么这种性质明显不受拉伸或旋转变换的影响。
另一个对区域描述有用的拓扑特性是连通分量的数量。如图4(b)显示了一个具有3个连通分量的区域。
图形中孔洞的数量 H H H 和连通分量的数量 C C C,可用于定义欧拉数 E E E:
E = C − H E = C - H E=C−H欧拉数也是一种拓扑特性。例如,图5所示的区域有分别等于 0 0 0 和 − 1 -1 −1 的欧拉数。

3. 纹理
描述区域的一种重要方法是量化该区域的纹理内容。尽管不存在纹理的正式定义,但在直觉上,这种描述子提供了诸如平滑度、粗糙度和规律性等特性的测度。图像处理中用于描述区域纹理的三种主要方法是统计法、结构法和频谱法。
统计法生成诸如平滑、粗糙、粒状等纹理特征。
结构法处理图像像元的排列,如基于规则间距平行线的纹理描述。
频谱法基于傅里叶频谱的特性,主要用于检测图像中的全局周期性,方法是识别频谱中的高能量的窄波峰。
① 统计法
描述纹理的最简方法之一是使用一幅图像或一个区域的灰度级直方图的统计矩。令 z z z 是表示灰度的一个随机变量,并令 p ( z i ) p(z_i) p(zi), i = 0 , 1 , 2 , . . . , L − 1 i=0,1,2,...,L-1 i=0,1,2,...,L−1 为相应的直方图,其中 L L L 是不同灰度级的数量。关于其均值的 z z z 的第n阶矩为
u n ( z ) = ∑ i = 0 L − 1 ( z i − m ) n p ( z i ) u_n(z) = \sum_{i=0}^{L-1}(z_i-m)^np(z_i) un(z)=i=0∑L−1(zi−m)np(zi)
式中, m m m 是 z z z 的均值(平均灰度):
m = ∑ i = 0 L − 1 z i p ( z i ) m = \sum_{i=0}^{L-1}z_ip(z_i) m=i=0∑L−1zip(zi)二阶矩是灰度对比度的测度,可用于建立相对平滑度的描述子;三阶矩是直方图斜度的测度;四阶矩是直方图相对平坦度的测度。
② 结构法
结构法的基本思想是,一个简单的“纹理基元”可借助一些规则用于形成更复杂的纹理模式,这些规则限制基元(或这些基元)的可能排列的数量。
③ 频谱法
对纹理描述有用的傅里叶频谱的三个特征:
(1) 频谱中突出的尖峰给出纹理模式的主要方向;
(2) 频率平面中尖峰的位置给出模式的基本空间周期;
(3) 采用滤波方法消除任何周期成分而留下非周期性图像元素,然后采用统计技术来描述。
五、SIFT(未完,待续)
https://www.cs.ubc.ca/~lowe/papers/ijcv04.pdf
以上全部内容参考书籍如下:
冈萨雷斯《数字图像处理(第三版)》
Joe Minichino、Joseph Howse《OpenCV 3计算机视觉Python语言实现(原书第2版)》