软工作业 - 数独
- 项目Github地址:https://github.com/Shadow-Priest/Sudoku
- 软工作业 - 数独
- 1. 思路描述
- 1.1 终局生成算法
- 1.2 数独求解算法
- 1.3 GUI界面 - 2. 具体设计
- 2.1 类的设计
- 2.2 单元测试
- 2.3 GUI设计 - 3. 性能分析
- 1.testAndSet()
- 2.print_to_buf() - 4. 代码说明
- 1. 思路描述
| PSP 2.1 | Personal Software Process Stages | 预估耗时(小时) | 实际耗时(小时) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 24.25 | 33.5 |
| Development | 开发 | ||
| · Analysis | · 需求分析 | 1 | 1 |
| · Design Spec | · 生成设计文档 | 1 | 0.5 |
| · Design Review | · 设计复审 | 0.25 | 0.0 |
| · Coding Standard | · 代码规范 | 2 | 1 |
| · Design | · 具体设计 | 2 | 4 |
| · Coding | · 具体编码 | 8 | 16 |
| · Code Review | · 代码复审 | 3 | 3 |
| · Test | · 测试 | 5 | 6 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 1 | 1 |
| · Size Measurement | · 计算工作量 | 0 | 0 |
| · Postmortem & Process Improvement Plan | · 事后总结,提出过程改进计划 | 1 | 1 |
| 合计 | 24.25 | 33.5 |
1. 思路描述
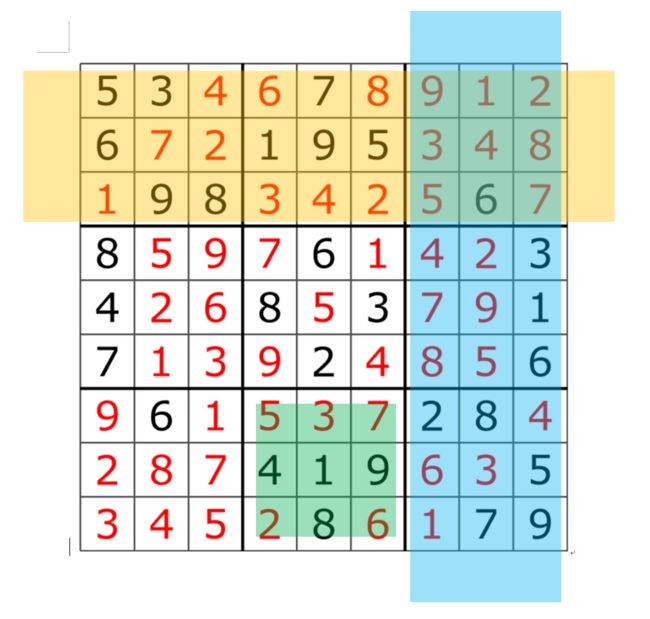
开始之前,我先明确了数独的术语
如下图,黄色掩板下即为大行(Band), 蓝色掩板下即为大列(Stack),绿色掩板下为一个宫(Block):
1.1 终局生成算法
进而查找了数独的生成算法
- 回溯法
- 矩阵交换 (随机性是否足够? 不够:生日悖论 200k时 碰撞概率超50%)
网上介绍的大多是回溯法,即一个格子一个格子的试,违背规则就撤回前一步。我认为效率很低。
在Google之后发现一个Github上的数独程序,做法是拿一个合法的数独终盘做矩阵变换。我以此为启发,加上一些思考设计了矩阵交换法
其基本思想是,对一个合法终盘做如下变换,不会破坏其合法性:
- 对同一大行(Band) 内的任意2行做交换
- 对同一大列(Stack) 内的任意2列做交换
- 对任意2个大行(Band) 做交换
- 对任意2个大列(Stack) 做交换
- 对任意2种数值 ,交换它们所有的元素
那么,我们要做的就是拿着1个可行解当作范本,构造行变换、列变换的映射向量,然后加上一个数值映射即可。终盘的生成完全依赖于映射向量,而映射向量的随即顺序直接用shuffle()洗牌方法即可。
如此一来,我们就不需要再不断地回溯来找可行解了。
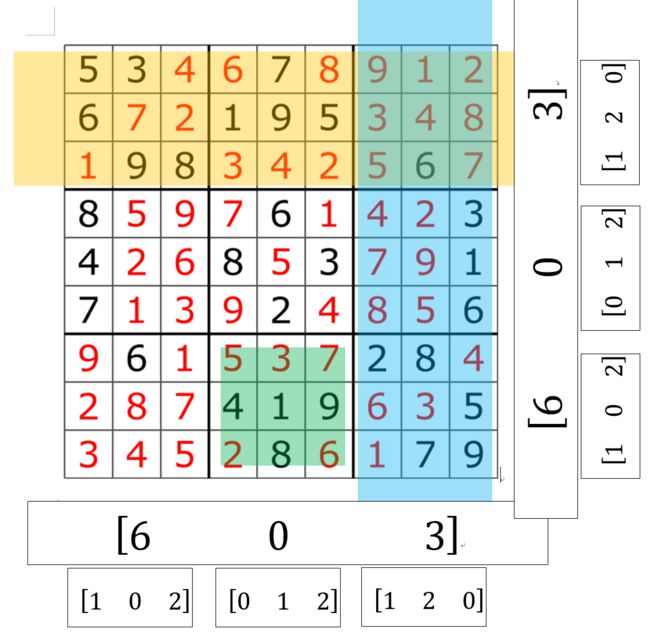
如下图,就是行变换、列变换的映射向量示例
1.2 数独求解算法
求解算法使用回溯法求解。在输入时记录已知值的位置,且维护3个列表来记录每行、列、block已存在的值。对每个空格,逐个尝试可能的取值.
显然,这样的求解算法比起生成所用的置换法来说慢了很多,但似乎这是能得到的最便于实现的方法。
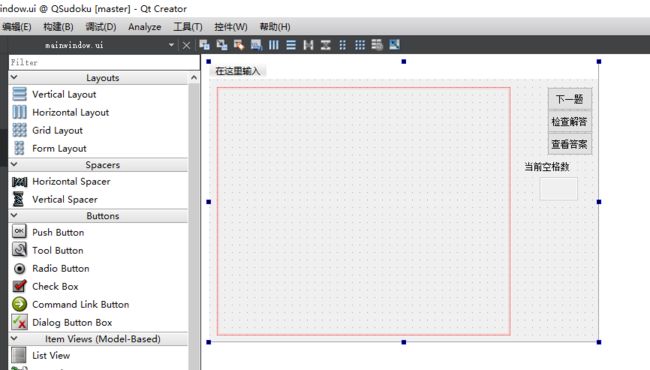
1.3 GUI界面
GUI界面我使用Qt 5图形库,其界面大致长这样:
点击“下一题”将会调用终局生成的算法,生成1个新终局。取出后对每个block随机选取2~7个元素挖掉。要求中有"总挖掉数介于30~60之间",所以随机出一个挖掉方案之后要检查一下,不行就重新挖
点击“检查解答”将会检查用户的解答。为了应付一题多解的情况,我们不以挖空前的相对照,而是直接根据数独的要求(行列宫填入1~9)来判断。
点击“查看答案”将会把生成的终局显示出来。
2. 具体设计
具体实现过程中,我设计了2个类,分别是:
-
LevelGenerator: 用于生成数独终局 -
PuzzleSolver: 用于读入、求解题目
而在命令行程序中,main函数的职能有:
- 识别参数
- 调用
LevelGenerator或是PuzzleSolver做生成或求解 - 把得到的结果取出,写入文件
参数识别我直接使用了开源库cxxopts(当然没忘了附带它的版权声明)[https://github.com/jarro2783/cxxopts],它能负责从参数列表中识别开关、读出参数值。
2.1 类的设计
LevelGenerator类可以生成数独终局,接受参数指明要生成的数目,将结果格式化成字符串存入缓冲区out_buffer中。它具有的方法:
-
mapping():从原始终局映射到新的终局 -
fix_first():固定首位 -
testAndSet():查重 -
generate_level():生成终局 -
print_to_buf():格式化输出到缓冲区
PuzzleSolver类用于做数独求解,指明谜题文件后调用solve()方法可以将结果格式化成字符串存入缓冲区out_buffer中。它具有的方法:
-
blockIndex():从行列坐标,求属于第几宫(block) -
markExistance():标记这一数值已存在 -
findNextValue():枚举出可能填入的值 -
load_puzzle():从文件读取谜题 -
solve():求解 -
print_to_buf():格式化输出到缓冲区
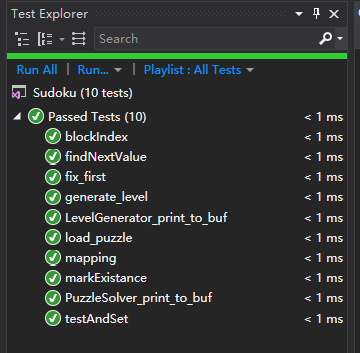
2.2 单元测试
我设计了10个单元测试项目,对LevelGenerator和PuzzleSolver这两个模块的方法进行了测试。单元测试的方法主要是:实例化一个对象-->设定其属性-->调用方法-->对返回值或对象属性做Assert
但由于我使用的Microsoft Visual Studio 2017,其分支覆盖功能仅提供给企业版使用,社区版不提供此功能,也没有替代的插件。因此没有分支覆盖率这一指标。
2.3 GUI设计
GUI界面我开启了一个新的工程,名为QSudoku。使用Qt 5图形库构建。
在可视化设计工具中添加几个固定的按钮,之后使用代码动态生成QLineEdit控件来当数独的格子。
之后将每个控件应该做的响应都写好代码即可
3. 性能分析
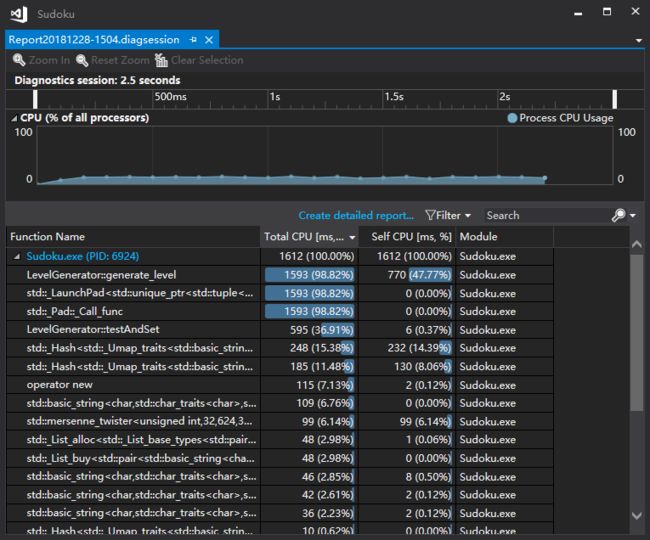
下图为生成1,000,000个数独终局的性能分析。
测试平台:
- CPU: Intel i7-6700k
- RAM: DDR4-2133MHz 16GB
- OS: Windows 10 1709 x64
可以看出2.213s完成这一速度还是很不错的
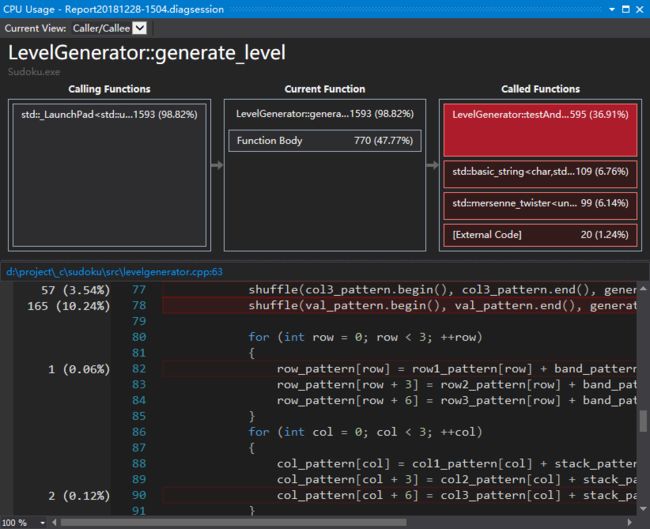
打开主要方法查看具体的时间消耗:
1. testAndSet()
看出耗时占比最大,耗费了36.9%的时间。这一函数是检查生成的终局是否重复而设计的。因为要求中着重强调了“不重复”,为了稳妥起见,则将每次生成的终局存入STL提供的unordered_map,每次生成都会从其中查询,若已存在则剔除这一重复项。
事实上,生成1,000,000个终局时大致会出现3~4个重复,若这样的碰撞率是可以容忍的,则这一testAndSet大可不必,但为保险还是留下了。而STL标准库的unordered_map已经是高度优化的,继续优化的空间不大。
2. print_to_buf()
很快注意到第二个耗时函数, 这是格式化输出到字符串缓冲区的函数。最初使用的是C++的流,在更换为sprintf做格式化输出后,其时间占比下降了约2%。
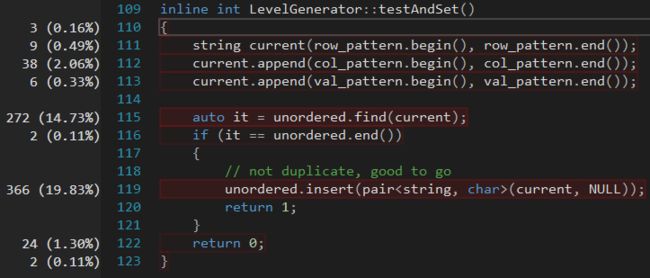
下图为耗时最长的函数:
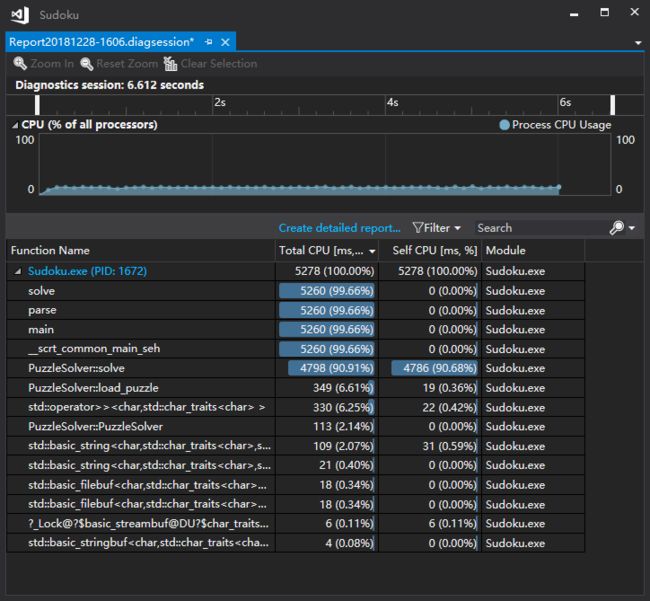
下图为对数独求解的性能分析:
可以看出递归的调用solve方法耗费的时间最长。
4. 代码说明
以下代码即是LevelGenerator终局生成器的关键代码。它主要的动作是对行、列、数值映射向量做洗牌,加上首位固定为7(我的学号末2位是51),判重。若不重复则格式化输出到缓冲字符串中。
void LevelGenerator::generate_level(int quantity)
{
for (int i = 0; i < quantity; ++i)
{
// 循环,直到生成了不重复的终局
for (;;)
{
shuffle(band_pattern.begin(), band_pattern.end(), generator);
shuffle(stack_pattern.begin(), stack_pattern.end(), generator);
shuffle(row1_pattern.begin(), row1_pattern.end(), generator);
shuffle(row2_pattern.begin(), row2_pattern.end(), generator);
shuffle(row3_pattern.begin(), row3_pattern.end(), generator);
shuffle(col1_pattern.begin(), col1_pattern.end(), generator);
shuffle(col2_pattern.begin(), col2_pattern.end(), generator);
shuffle(col3_pattern.begin(), col3_pattern.end(), generator);
shuffle(val_pattern.begin(), val_pattern.end(), generator);
fix_first(7);
// 若是新的终局,停止循环
if (testAndSet()) { break; }
// 否则计数(供分析使用)
duplicate_times_count++;
}
// 映射
mapping(original, gen1);
// 写入缓存
print_to_buf(gen1);
out_buffer += '\n';
}
}
下面是使用PuzzleSolver求解数独的调用者。
首先实例化对象,提供谜题文件的路径。
不断循环地load_puzzle()来读入谜题,直到文件尾
调用solve进行求解。
最后,再将对象中缓冲区的文本写入文件。
// solve
void solve(string file_path)
{
PuzzleSolver pz(file_path);
while (pz.load_puzzle()) { pz.solve(0, 0); }
if (!pz.out_buffer.empty())
pz.out_buffer.erase(pz.out_buffer.size() - 2); // strip last 2 LF
// write to file
ofstream file;
file.open(FILE_OUT, ios::out);
file << pz.out_buffer;
file.close();
}
下面是solve()函数代码:
其主要动作是跳过已知值,递归的枚举未知值
int PuzzleSolver::solve(int row, int col)
{
if (col == 9) { row++; col = 0; }
// skip fixed
while (row <= 8 && isFixed[row][col])
{
col++;
if (col == 9) { row++; col = 0; }
}
// on completion
if (row > 8)
{
print_to_buf(puzzle);
out_buffer += '\n';
return 1;
}
while (puzzle[row][col] = findNextValue(row, col, puzzle[row][col] + 1))
{
markExistance(row, col, puzzle[row][col], 1);
if (solve(row, col + 1))
{
return 1;
}
markExistance(row, col, puzzle[row][col], 0);
}
return 0;
}