图形绘制
离散函数图形:
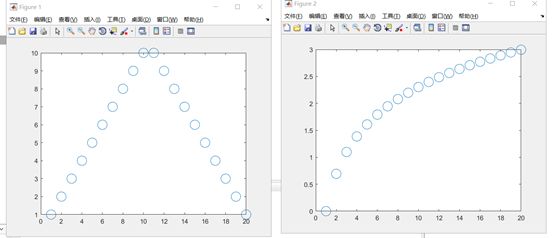
例:离散数据和离散函数可视化(离散数据作图方式)
X1=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]; Y1=[1,2,3,4,5,6,7,8,9,10,10,9,8,7,6,5,4,3,2,1]; figure(1) plot(X1,Y1,'o','MarkerSize',15) %作图函数,’o’为图案,MarkerSize设置图案大小15 X2=1:20; Y2=log(X2); figure(2) plot(X2,Y2,'o','MarkerSize',15)
连续函数图形:
在matlab中没有真正的连续函数,只能通过离散的量表示。为了更形象体现函数的规律变化,有两种方法。1是更加细致的对离散区间进行划分,更加趋近函数的连续变化特性。2是把两个离散的点进行连接,以两点之间的直线近似表示。
例:连续函数可视化
subplot(m,n,p) 将当前图窗划分为 m×n 网格,并在 p 指定的位置创建坐标区。MATLAB® 按行号对子图位置进行编号。第一个子图是第一行的第一列,第二个子图是第一行的第二列,依此类推。如果指定的位置已存在坐标区,则此命令会将该坐标区设为当前坐标区。
xlim(limits) 设置当前坐标区或图的 x 坐标轴范围。将 limits 指定为 [xmin xmax] 形式的二元素向量,其中 xmax 大于 xmin。
X1=(0:12)*pi/6; Y1=cos(3*X1); X2=(0:360)*pi/180; Y2=cos(3*X2); figure(1) subplot(2,2,1); %将figure创建的图形区划分为2x2,并在1创建图形 plot(X1,Y1,'o','MarkerSize',3); xlim([0 2*pi]) %将坐标轴范围设置为0-2*pi subplot(2,2,2); plot(X1,Y1,'LineWidth',2); xlim([0 2*pi]) subplot(2,2,3); plot(X2,Y2,'o','MarkerSize',3); xlim([0 2*pi]) subplot(2,2,4); plot(X2,Y2,'LineWidth',2); xlim([0 2*pi])
图形绘制的基本步骤和实例:
1,数据准备, 产生自变量采样向量,计算相应的值向量
2,选定图形窗口和子图位置,默认情况下,matlab系统绘制图形为figure1,figure2…….
3,调用绘图函数绘制图形,如plot();
4,设置坐标轴范围,刻度和坐标网格
5,利用对象属性值或图形窗口工具栏设置线型,标记类型和大小等
6,添加图形注释,例如图名,坐标名称,图例,文字说明等
7,图形的导出和打印
例:设函数 ,绘制 的图像。
x=-pi/2:0.01:pi/2; y=x+sin(x)+exp(x); %1数据准备 plot(x,y); %2,3默认选定figure1,绘制图形
会有如下结果
进行修改:
x=-pi/2:0.01:pi/2; y=x+sin(x)+exp(x); plot(x,y,'-ro') %‘-ro’ 5将曲线设置为红色 grid on %4可以在坐标区绘制网格线
grid on 显示 gca 命令返回的当前坐标区或图的主网格线。主网格线从每个刻度线延伸。
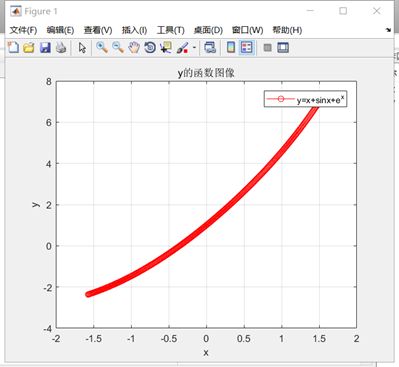
补充说明上的修改:
x=-pi/2:0.01:pi/2; y=x+sin(x)+exp(x); plot(x,y,'-ro') grid on title('y的函数图像'); xlabel('x'); ylabel('y'); legend('y=x+sinx+e^x'); %四个都为注释说明类的属性,由下图可知功能