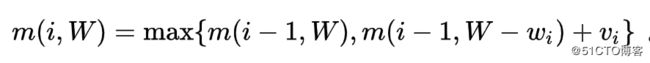问题:
假设你要去野营。你有一个容量为6磅的背包,需要决定该携带下面的哪些东西。其中每样东西都有相应的价值,价值越大意味着越重要:
•水(重3磅,价值10);
•书(重1磅,价值3);
•食物(重2磅,价值9);
•夹克(重2磅,价值5);
•相机(重1磅,价值6)。
请问携带哪些东西时价值最高?
思路:
这是一个典型的背包问题,求解此类问题,通常会使用动态规划法。不要被名字吓到,其实并不难。下面我们来讲解该算法。
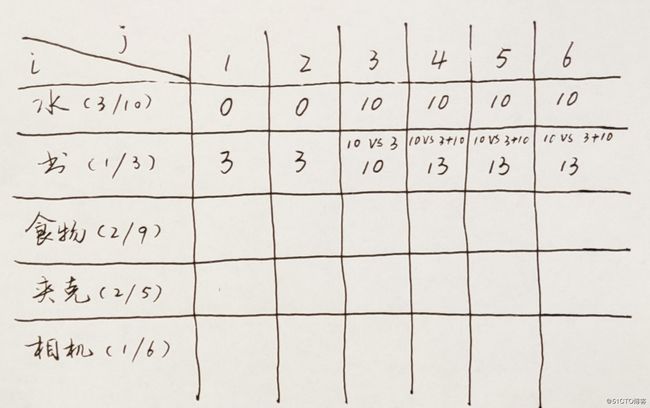
动态规划算法都是从网格开始的,我们先画一个如下的网格: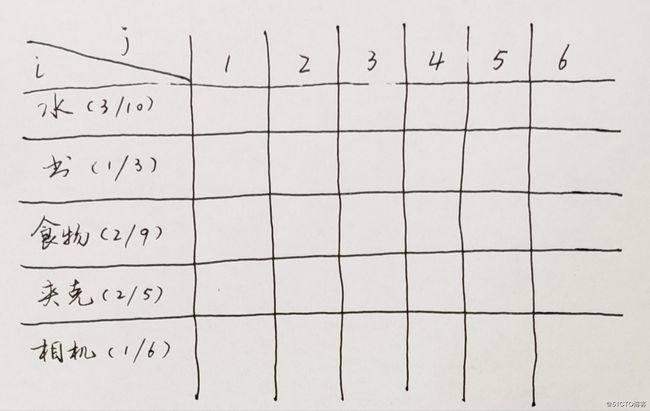
网格的每一行表示一件物品,每一列表示不同容量的背包,这里从1到6。物品后面的括号里标注了物品的重量及价值。
下面开始求解。
我们需要从左至右,从上至下填充每一个单元格。
第一个单元格表示,1磅容量的背包,现在要装入第一件物品水,我们发现水的重量是3磅,装不进去,此时,该单元格填充0,表示不能装入任何物品。
第二个单元格也是一样。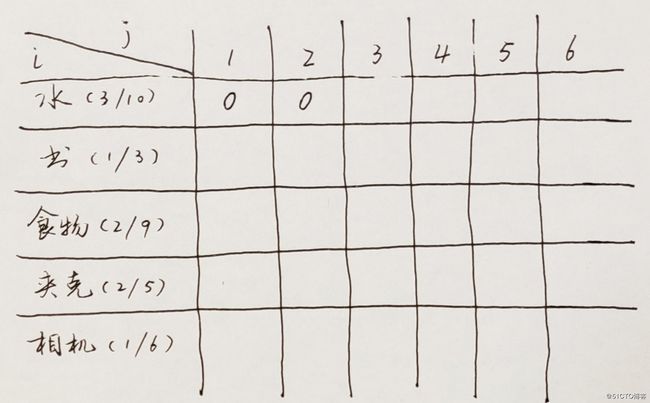
到第三个单元格时,背包容量是3磅,水的重量也是3磅,刚好可以装下,此时,填充单元格,将水的价值填入。第四个单元格时,背包容量是4磅,不仅可以装下水,还有1磅的余量,但我们目前只有水一件物品,所以余下的空间也不能用,因此,背包能装的最大价值还是3磅的水,价值是10。第五,第六单元格也是如此。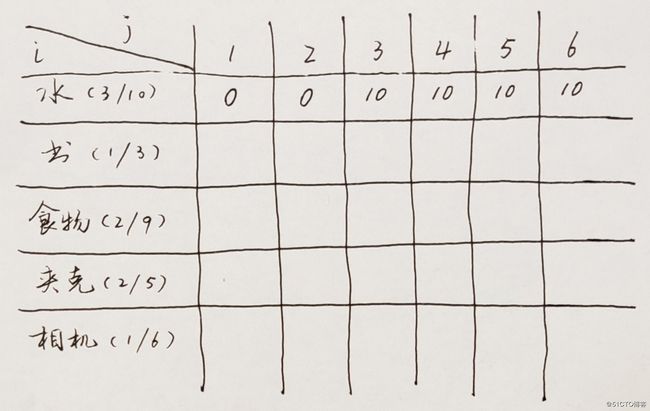
此时,6磅背包最大可以携带价值为10的物品。接下来,我们准备装入第二件物品。
第二件物品是书,重量是1磅,背包容量是1磅时刚好可以放下。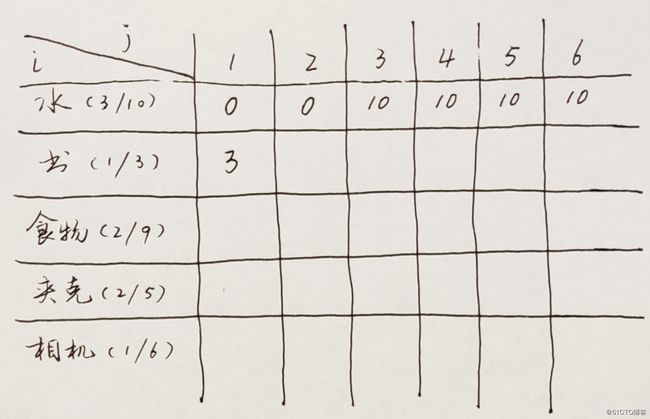
接着是2磅容量的背包,也能放下书。但当背包容量到3时,有情况发生了。
此时我们需要考虑一下,到底是放1磅重的书呢,还是3磅重的水,显然,水的价值更大。所以10 vs 3的结果明显是10胜出,所以第二行第三个单元格的最大价值是10。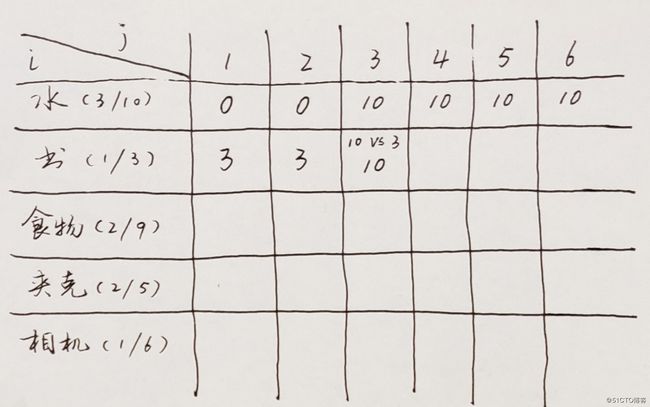
第四个单元格的情况又有变化。我们此时的背包容量是4磅,书的重量是1磅,如果装了书,那么余下的容量是3磅,我们看一下前一行,背包容量是3磅时的最大价值为10。这就意味着,这一个单元格可以同时放下书和水,共计4磅重量,价值为3+10=13。我们跟前一行的第四单元格对比一下,之前的最大价值是10。现在13 vs 10,明显13胜出,所以,第二行第四单元格我们的最大价值是13。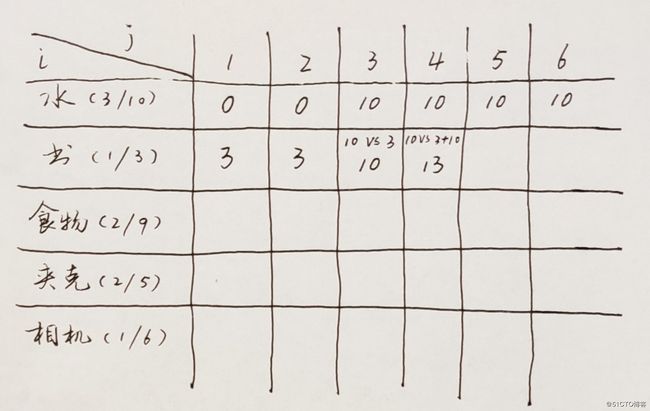
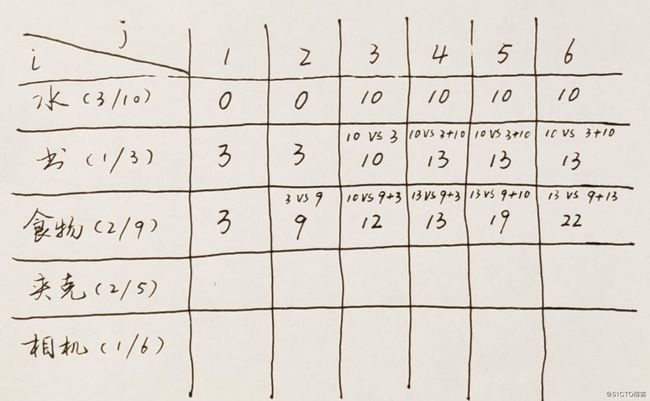
接着我们开始算第三行。
第三行第一单元格是放不下食物的,所以沿用前一行对应单元格的价值3。
第二单元格时,有两种选择,一是沿用前一行的物品书,二是放入食物,对比一下价值,很明显应该放入价值9的食物。
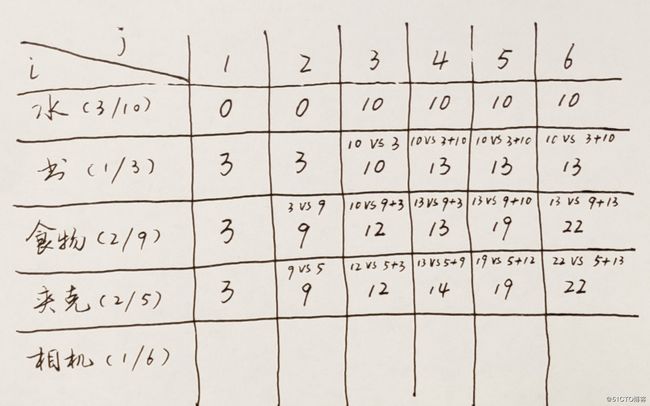
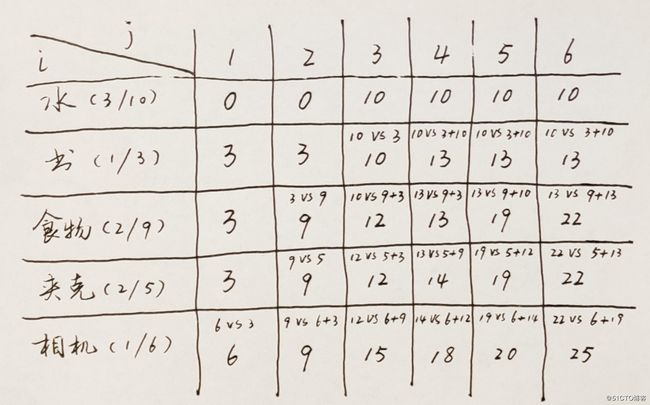
当我们填充完后,最后一行最后一个单元格中的价值便是我们能达到的最大价值。
比如最后一行,最后一个单元格。我们的填充方法是:
先取到前一行相同容量背包的价值,这里是22;
当前物品的价值是6,重量是1,如果将该物品放入背包中,则余下容量是5。
前一行背包容量为5时的最大价值是19,即之前5磅背包最多可以放下价值19的物品,再加上当前物品的价值6,合计能放下价值19+6=25的物品;
22 vs 25,取最大的值,则最终能放下价值25的物品。
解答:
有了算法,我们便可以用代码来实现:
这里我们用php来实现,首先我们把问题先整理出来,如下:
$goods = array(
array("name" => "水", "weight" => 3, "value" => 10),
array("name" => "书", "weight" => 1, "value" => 3),
array("name" => "食物", "weight" => 2, "value" => 9),
array("name" => "夹克", "weight" => 2, "value" => 5),
array("name" => "相机", "weight" => 1, "value" => 6),
);
$maxWeight = 6; //背包最大容量接着,开始写算法:
$table = array();// 表格
foreach ($goods as $i => $good) {
for ($j = 1; $j <= $maxWeight; $j++) {
// 填充第一行
if ($i == 0) {
if ($j < $good['weight']) {
$table[$i][$j] = 0;
} else {
$table[$i][$j] = $good['value'];
}
} else {
$v1 = $table[$i - 1][$j];
if ($j < $good['weight']) { // 当装不下时,以前一格为准
$table[$i][$j] = $v1;
} else {
// 1.前一行同列的值;2.当前物品价值+余下重量的最大价值。这两者取最大值
if ($j == $good['weight']) {
$preMax = 0;
} else {
$preMax = $table[$i - 1][$j - $good['weight']];
}
$v2 = $good['value'] + $preMax;
$table[$i][$j] = max($v1, $v2);
}
}
}
}
print_r($table);我们打印了表格,结果如下,可以对比一下手算的结果:
Array
(
[0] => Array
(
[1] => 0
[2] => 0
[3] => 10
[4] => 10
[5] => 10
[6] => 10
)
[1] => Array
(
[1] => 3
[2] => 3
[3] => 10
[4] => 13
[5] => 13
[6] => 13
)
[2] => Array
(
[1] => 3
[2] => 9
[3] => 12
[4] => 13
[5] => 19
[6] => 22
)
[3] => Array
(
[1] => 3
[2] => 9
[3] => 12
[4] => 14
[5] => 19
[6] => 22
)
[4] => Array
(
[1] => 6
[2] => 9
[3] => 15
[4] => 18
[5] => 20
[6] => 25
)
)到这里还没有结束,我们还得知道要装哪些物品,所以还需要一个回溯。
从后向前进行逆推,如果当前单元格的价值与前一行同列单元格的价格相同,说明当前物品没有加入到背包中,计为$x[$i]=0;
否则,就计为$x[$i]=1,并从总重量中减去当前物品的重量;
当回溯到第一件物品时,看下$j的值,如果非负,说明第一件物品是入选物品计为1,否则计为0。
$j = $maxWeight;
$n = count($goods);
$x = array();// 物品数组
for ($i = $n - 1; $i >= 0; $i--) {
if ($i > 0) {
if ($table[$i][$j] == $table[$i - 1][$j]) {
$x[$i] = 0;
} else {
$x[$i] = 1;
$j -= $goods[$i]['weight'];// 每次扣减当前物品的重量
}
} else {
$x[$i] = $j >= 0 ? 1 : 0;// 如果最后发现$j是有值的,那便是第1个物品
}
}
ksort($x);// 把回溯的过程改为顺序
foreach ($x as $key => $val) {
if ($val != 0) {
print_r($goods[$key]);
}
}结果如下:
Array
(
[name] => 水
[weight] => 3
[value] => 10
)
Array
(
[name] => 食物
[weight] => 2
[value] => 9
)
Array
(
[name] => 相机
[weight] => 1
[value] => 6
)以下是Golang的实现,算法一样,只是换了种语言实现而已
package main
import (
"fmt"
"math"
)
type Goods struct {
Name string
Weight int
Value int
}
var GoodsList []Goods // 物品列表
var maxWeight = 6 // 背包最大容昊
func main() {
GoodsList = []Goods{
{Name: "水", Weight: 3, Value: 10},
{Name: "书", Weight: 1, Value: 3},
{Name: "食物", Weight: 2, Value: 9},
{Name: "夹克", Weight: 2, Value: 5},
{Name: "相机", Weight: 1, Value: 6},
}
table := make([][]int, len(GoodsList))
for i, goods := range GoodsList {
table[i] = make([]int, maxWeight+1)
for j := 1; j <= maxWeight; j++ {
if i == 0 {
if goods.Weight > j {
table[i][j] = 0
} else {
table[i][j] = goods.Value
}
} else {
v1 := table[i-1][j]
if goods.Weight > j {
table[i][j] = v1
} else {
preMax := 0
if j == goods.Weight {
preMax = 0
} else {
preMax = table[i-1][j-goods.Weight]
}
v2 := goods.Value + preMax
//fmt.Println(v1, v2, goods)
table[i][j] = int(math.Max(float64(v1), float64(v2)))
}
}
}
}
fmt.Println(table)
goodsNum := len(GoodsList)
j := maxWeight
x := make([]int, goodsNum)
for i := goodsNum - 1; i >= 0; i-- {
if i > 0 {
if table[i][j] == table[i-1][j] {
x[i] = 0
} else {
x[i] = 1
j -= GoodsList[i].Weight
}
} else {
if j >= 0 {
x[i] = 1
} else {
x[i] = 0
}
}
}
for key, value := range x {
if value == 1 {
fmt.Println(key, GoodsList[key])
}
}
}输出
[[0 0 0 10 10 10 10] [0 3 3 10 13 13 13] [0 3 9 12 13 19 22] [0 3 9 12 14 19 22] [0 6 9 15 18 20 25]]
0 {水 3 10}
2 {食物 2 9}
4 {相机 1 6}