如果写这篇文章仅仅是介绍层次分析法的理论,显得完全没有必要。层次分析法作为最早接触到的一批算法,登山、旅游的决策案例听过太多遍了。
本文想讲一讲层次分析法在打分机制上的应用。
一、基础概念
详细内容查看AHP层次分析法的步骤和方法
二、层次分析法在打分机制的应用
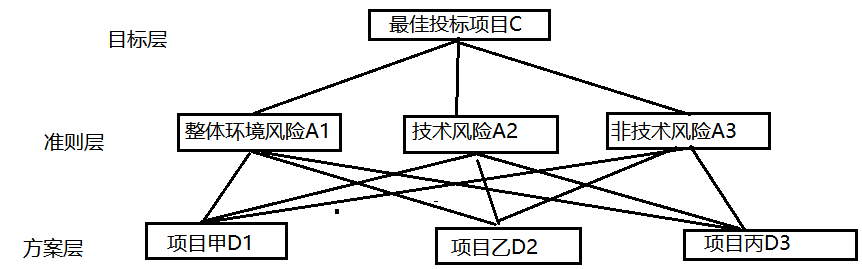
(1)层次结构
层次分析法绕不开的第一步就是确定层次结构.(需要特征在三个及三个以上,否则无法满足一致性检验)
(2)对比矩阵
建立对比矩阵C,判断准则层三个特征对项目而言的重要程度。
使用专家评分的方式,评定对于项目而言各个特征的比较分值。
例如下图第一行技术风险A2比环境风险A1重要很多,非技术风险A3比环境风险A1重要一点。
矩阵C按列归一化处理,新矩阵B按行求和/n得到每个特征的权重:0.64794686, 0.12218196, 0.22987118
该矩阵满足一致性检验,CR=0.003
(3)项目评分
方法一:专家继续评分
此方法适用方案层有三个及以上的参与者。理由是RI在n=1,2时,值为0,会导致一致性检验不满足要求。
A1条件下
整体环境风险A1下,三个候选人D1、D2、D3的比较。
| A1 | D1 | D2 | D3 |
|---|---|---|---|
| D1 | 1 | 3 | 1/5 |
| D2 | 1/3 | 1 | 1/7 |
| D3 | 5 | 7 | 1 |
满足一致性检验,CR = 0.056740233073197095
三个项目在A1条件下,各自的权重为:0.193, 0.083, 0.723。
A2条件下
技术风险A2下,三个候选人D1、D2、D3的比较
| A2 | D1 | D2 | D3 |
|---|---|---|---|
| D1 | 1 | 1/4 | 1/2 |
| D2 | 4 | 1 | 3 |
| D3 | 2 | 1/3 | 1 |
满足一致性检验,CR = 0.015807980379472106
三个项目在A1条件下,各自的权重为:0.137, 0.623, 0.239
A3条件下
非技术风险A3下,三个候选人D1、D2、D3的比较
| A3 | D1 | D2 | D3 |
|---|---|---|---|
| D1 | 1 | 1/3 | 5 |
| D2 | 3 | 1 | 7 |
| D3 | 1/5 | 1/7 | 1 |
满足一致性检验,CR = 0.056475713035283585
三个项目在A1条件下,各自的权重为:0.283, 0.643, 0.074
三个项目评分
项目甲D1在环境风险A1、技术风险A2、非技术风险A3下的分值分别为0.193、0.137、0.283。所以项目D1的总得分为=分值 * 特征权重。
SCORE = 0.193 * 0.64794686 + 0.137 * 0.12218196 + 0.283 * 0.22987118 = 0.20696492
同理计算出项目乙得分0.27802246,项目丙得分0.51501263。所以丙是最合适的选择。
方法二:直接打分模式
项目甲D1在环境风险A1、技术风险A2、非技术风险A3三个方面的得分分别为72, 78, 88;
项目甲D2在环境风险A1、技术风险A2、非技术风险A3三个方面的得分分别为68, 90, 94;
项目甲D3在环境风险A1、技术风险A2、非技术风险A3三个方面的得分分别为98, 80, 78;
项目总得分为=分值 * 特征权重。
甲乙丙三个项目得分分别为:77.49、79.93、86.43,丙为最优选择。
方法三:模糊评分法
已经根据层次分析计算出每个特征的权重。
方法一是采用方案层在每个特征下的比较;方案二是直接对每个项目打分;但这类打分人工随意性比较大。还可以采用模糊评价法,设置评价集V={很好,好,一般,差},找20个人来打分,数值为打这些分的人数。
| D1 | 很好 | 好 | 一般 | 差 |
|---|---|---|---|---|
| 整体环境风险A1 | 5 | 4 | 2 | 9 |
| 技术风险A2 | 8 | 4 | 8 | 0 |
| 非技术风险A3 | 4 | 9 | 1 | 6 |
对矩阵归一化后为M,得分 = 权重 * M,再归一化 。
D1 = [0.23, 0.23, 0.17, 0.37]
同理计算出项目乙D2,项目丙D3的模糊得分
D2 = [0.17, 0.31, 0.40, 0.12]
D3 = [0.46, 0.18, 0.24, 0.12]
说明项目甲23%程度为很好,23%程度为好,17%程度为一般,37%程度为差;
说明项目乙17%程度为很好,31%程度为好,40%程度为一般,12%程度为差;
说明项目丙46%程度为很好,18%程度为好,24%程度为一般,12%程度为差;
要求很好、好的概率在60%以上,因此项目丙是最优选择。
三、层次分析法评分升级
觉得三个特征还能继续深入。扩展准则层。
第一步:建立A1,A2,A3三个大特征的对比矩阵,计算三个特征的权重W1、W2、W3。
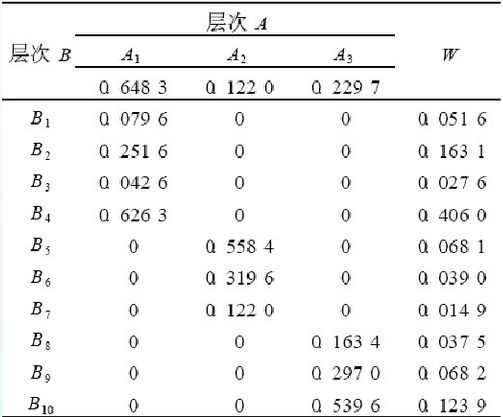
第二步:特征A1下有B1、B2、B3、B4四个特征,建立B1、B2、B3、B4的对比矩阵,计算特征的权重w11,w12,w13,w14;
特征A2下有B5、B6、B7三个特征,建立B5、B6、B7的对比矩阵,计算特征的权重w21,w22,w23;
特征A3下有B8、B9、B10三个特征,建立B8、B9、B10的对比矩阵,计算特征的权重w31,w32,w33。
B1、B2、B3、B4,...,B10的特征权重为w11W1,w12W1,w13W1,...,w33W3
第三步:分值计算。
先设置项目在B系列特征的得分a1,a2,...,a10,项目总得分为sum(权重*得分)。
四、优缺点的思考
(1)以上专家评分是在满足逻辑的前提下,一堆乱打的分值。所以层次分析法的打分质量的好坏影响判断,专家打分人为因素太强,解释性不够。
(2)准则层涉及的特征不宜过多,特征太多人工写分数很麻烦。
参考资料
层次分析法在项目风险分析中的应用
绝对打分方法