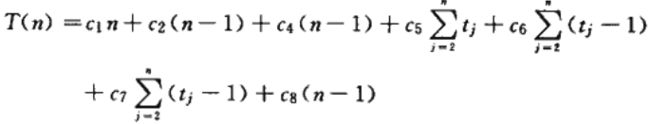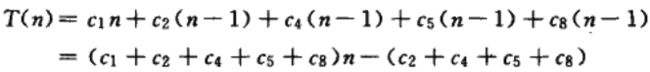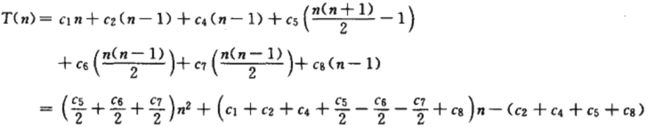版本记录
| 版本号 | 时间 |
|---|---|
| V1.0 | 2017.08.11 |
前言
将数据结构和算法比作计算机的基石毫不为过,追求程序的高效是每一个软件工程师的梦想。下面就是我对算法方面的基础知识理论与实践的总结。感兴趣的可以看上面几篇。
1. 算法简单学习(一)—— 前言
插入排序 insertion - sort
插入排序是一个针对少量元素进行排序的有效算法,下面我们先看一下插入排序的模型。
1. 问题描述
输入数据:n个数 (a1, a2, ... , an)
输出数据:对这n个数据重新排序,使得a1' ≤ a2' ≤ ... ≤ an'。这里待排序的数也称为关键字。
2. 算法模型
开始打牌时,左边的手是空着的,牌面朝下放在桌子上,接着,一次从桌子上摸起一张牌,并将它插入左手一把牌中的正确位置,为了找到这个牌的正确位置,要将它与手中已有从右向左进行比较,如上图所示。无论什么时候左手中的牌都是排序好的,而这些牌原先都是桌子上那副里最顶上的一些牌。
3. 算法伪代码
下面我们就看一下算法伪代码。
//insertion sort
1 for j ← 2 to length[A]
2 do key ← A[j]
3 //insert A[j] into the sorted sequence A[1 ... j - 1]
4 i ← j - 1
5 while i > 0 and A[i] > key
6 do A[i + 1] ← A[i]
7 i ← i - 1
8 A[i + 1] ← key
4. 循环不变式与插入算法的正确性
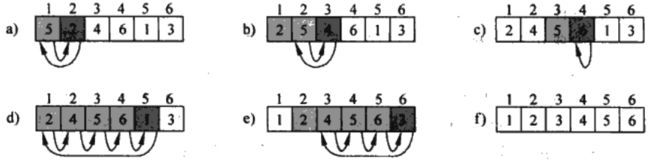
下面看这个数组 A = [5, 2, 4, 6, 1, 3],下标j指示了待插入到手中的当前牌,在外层for循环(循环变量为j)的每一轮迭代的开始,包含元素A[1 ... j - 1]的子数组构成了左手中当前已经排好的序的一手牌,元素A[j + 1 ... n]对应于桌子上的那堆没有抓起来的牌。
下面以循环不变式(loop invariant)的形式,来表达A[1 ... j - 1]的这些性质。在过程第1 ~ 8行伪代码中,在每一轮迭代的开始,子数组A[1 ... j - 1]中包含了最初位于A[1 ... j - 1]但是目前已经排好序,循环过程如下所示。
上图中黑色方框里面的值取自A[j]的关键字值,在过程第5行的测试中,将它与左边阴影框中的各个值进行比较。
循环不变式的三个性质:
- 初始化: 它在循环的第一轮迭代开始之前,应该是正确的。
- 保持 : 如果在循环的某一次迭代开始之前它是正确的,那么,在下一次迭代开始之前,它也应该保持正确。
- 终止 : 当循环结束时,不变式给我们有一个有用的性质,有助于表明算法是正确的。
下面就证明一下这些性质的正确性。
初始化 : 首先看第一轮迭代开始之前的正确性,此时
j = 2,而子数组为A[1 ... j - 1],则只包含一个元素A[1],实际上就是最初在A[1]中的那个元素,这个子数组已经是排序好的了,证明第一次迭代开始之前是成立的。保持 :看第二个性质,证明每一轮循环都使循环不变式保持成立,从非形式化的意义上看,外层for循环的循环体中,要将
A[j - 1],A[j - 2],A[j - 3]等元素向右移动一个位置,直到找到A[j]的适当位置时为止(第4 ~ 7)行,这时将A[j]的值插入(第 8 行)。如果要证明这个性质不成立就需要证明while循环有一个循环不成立,这里就不证明了。终止: 当
j = n + 1的时候外层for循环结束,将j替换为n + 1,就有子数组A[1..n]包含了原先A[1..n]中的元素,但是现在已经排好序了,就已经是整个数组了,也就意味这个数组是正确的。
5. 算法分析
算法分析即指对一个算法所需要的资源进行预测,内存、通信宽带或计算机硬件等资源偶尔会是我们主要关心的,但是通常,资源就是指我们希望测度的计算时间。在分析一个算法之前,要建立有关实现技术的模型,包括描述所用资源及代价的模型。
插入排序过程的时间开销和输入有关,不同个数的排序时间消耗一定不同。即使输入个数相同,时间也不一定相同,还和它们已排列的程度有关。
可以将运行时间表示为运行时间和输入规模的函数。
- 输入规模:这个因素与具体问题有关。
- 运行时间:指在特定输入时,所执行的基本操作数或步数,可以很方便的定义独立于具体机器的步骤概念。目前先假定执行一行伪代码花费的时间都是常量
ci。
对 j = 2, 3, ..., n , n = length[A],设tj为第 5行中while的测试次数,循环体要比测试少一次,即不满足条件退出,所得的占用时间如下所示。
下面我们把这些时间相加,可得。
上面的表达式就是运行时间的总和。
从上面式子可以看到,即使规模相同,那么时间长度也与该规模下数据的输入情况有关。下面我们看几种特殊情况。
- 假定输入数组已经排好序
这种情况对于 j = 2, 3, ... , n中的每一个值,都会发现,在第 5 行汇总,当 i 取其初始值j - 1时,都有A[i] ≤ key,于是对应j = 2, 3, ... , n中有tj = 1,则可以简化最佳运行时间为:
这个时候时间就可以简化为T(n) = an + b,其中a, b都是与ci有关的常数。
- 假定输入数组是逆序排列
这个时候就需要我们将每一个元素A[j]与整个已排序的子数组A[1 ... j - 1]中的每一个元素进行比较,因此,对于 j = 2, 3, ... , n有tj = j,那么时间函数变化为:
我们简化为 T(n) = an ^ 2 + bn + c,a, b, c均为与ci有关的常数,整个函数是关于n的二次函数。
6. 插入排序的最坏情况和平均情况分析
上面我们可以看到最坏情况就是输入的是逆序的情况,最好的情况就是输入的是排好顺序的情况,我们一般考虑的就是最坏的运行时间。
- 知道一个算法的运行最坏情况,就是知道了算法的时间上限,就不用担心它会变的更坏了。
- 对于某些算法来说,最坏的情况出现的情况还是相当频繁的,例如当我们在数据库里面检索一条不存在的信息时,就是出现了算法的最坏情况。
- 这里还要说一下平均情况,这里的平均情况就是数组中
A[1 ... j - 1]中一半元素小于A[j],另外一半元素大于A[j],因此,这里有tj = j / 2,在计算时间复杂度你就会发现它仍然是一个二次函数,与最坏情况下的运行时间是一样的。
7. 增长的量级
下面我们对上面提出的时间表达式进一步进行首相,得到的就是运行时间的增长率 (rate of growth),或称为增长的量级(order of growth),这样我们只考虑最高次项而忽略其他项,同时也忽略最高次项的系数,所以上面我们总结的最坏情况的表达式就为O(n^2)。
一般认为,如果一个算法最坏情况运行时间要比另外一个算法的低,就认为它的效率更高。
8. 代码实现
下面我们就看一下代码实现。
先建立一个C工程。
下面我们看一下代码实现。
乱序
#include
#include
#include
int main(int argc, const char * argv[])
{
int a[6] = {5, 2, 4, 6, 1, 3};
int length = sizeof(a)/sizeof(a[0]);
clock_t startTime, endTime;
startTime = clock();
for (int j = 1; j <= length - 1; j++) {
int i = j - 1;
int key = a[j];
while (i >= 0 && a[i] > key) {
a[i + 1] = a[i];
i --;
a[i + 1] = key;
}
}
endTime = clock();
for (int k = 0; k < length; k++) {
printf("%d\n",a[k]);
}
printf("运行时间为%ld\n", endTime - startTime);
return 0;
}
下面看输出结果
1
2
3
4
5
6
运行时间为3
Program ended with exit code: 0
顺序
#include
#include
#include
int main(int argc, const char * argv[])
{
int a[6] = {1, 2, 3, 4, 5, 6};
int length = sizeof(a)/sizeof(a[0]);
clock_t startTime, endTime;
startTime = clock();
for (int j = 1; j <= length - 1; j++) {
int i = j - 1;
int key = a[j];
while (i >= 0 && a[i] > key) {
a[i + 1] = a[i];
i --;
a[i + 1] = key;
}
}
endTime = clock();
for (int k = 0; k < length; k++) {
printf("%d\n",a[k]);
}
printf("运行时间为%ld\n", endTime - startTime);
return 0;
}
下面看一下输出结果
1
2
3
4
5
6
运行时间为1
Program ended with exit code: 0
倒序
#include
#include
#include
int main(int argc, const char * argv[])
{
int a[6] = {6, 5, 4, 3, 2, 1};
int length = sizeof(a)/sizeof(a[0]);
clock_t startTime, endTime;
startTime = clock();
for (int j = 1; j <= length - 1; j++) {
int i = j - 1;
int key = a[j];
while (i >= 0 && a[i] > key) {
a[i + 1] = a[i];
i --;
a[i + 1] = key;
}
}
endTime = clock();
for (int k = 0; k < length; k++) {
printf("%d\n",a[k]);
}
printf("运行时间为%ld\n", endTime - startTime);
return 0;
}
下面看输出结果
1
2
3
4
5
6
运行时间为3
Program ended with exit code: 0
后记
未完,待续~~~