4.3 利用数组进行数据处理
编程环境:jupyter Notebook
矢量化:用数组表达式代替循环的方法
***在一组值上计算函数sqrt(x2+y2)
np.meshgrid函数接受两个一维数组,并产生两个二维矩阵
import numpy as np
points = np.arange(-5,5,0.01)
xs,ys = np.meshgrid(points,points)
z = np.sqrt(xs**2 + ys **2)
[[7.07106781 7.06400028 7.05693985 ... 7.04988652 7.05693985 7.06400028]
[7.06400028 7.05692568 7.04985815 ... 7.04279774 7.04985815 7.05692568]
[7.05693985 7.04985815 7.04278354 ... 7.03571603 7.04278354 7.04985815]
...
[7.04988652 7.04279774 7.03571603 ... 7.0286414 7.03571603 7.04279774]
[7.05693985 7.04985815 7.04278354 ... 7.03571603 7.04278354 7.04985815]
[7.06400028 7.05692568 7.04985815 ... 7.04279774 7.04985815 7.05692568]]
**将条件逻辑表述为数组运算
假设我们有一个布尔数组和两个值数组
xarr = np.array([1.1,1.2,1.3,1.4,1.5])
yarr = np.array([2.1,2.2,2.3,2.4,2.5])
cond = np.array([True,False,True,True,False])
条件: 根据cond中的值选取xarr和yarr的值:当cond值为True时,选取xarr的值,否则从yarr中选取
result = [(x if c else y) for x,y,c in zip(xarr,yarr,cond)]
print(result)
[1.1, 2.2, 1.3, 1.4, 2.5]
numpy.where函数时三元表达式 x if condition else y的矢量化版本
现在我们使用numpy.where来实现该功能
print(np.where(cond,xarr,yarr))
[1.1 2.2 1.3 1.4 2.5]
np.where的第二个和第三个参数也可以是标量值,实现:随机生成的矩阵所有正值替换为2,将所有负值替换为-2
arr = np.random.randn(4,4)
print(arr)
[[-0.44648801 2.2911988 0.22864356 -0.4295595 ]
[ 0.41009951 -2.58334298 0.25169705 0.84350217]
[ 0.23906103 1.68893028 1.1369141 0.0551288 ]
[ 0.33207166 0.239592 0.87422568 -0.07501011]]
print(np.where(arr > 0,2,-2))
[[-2 2 2 -2]
[ 2 -2 2 2]
[ 2 2 2 2]
[ 2 2 2 -2]]
np.where也可以将标量和数组结合起来
print(np.where(arr>0,2,arr))
[[-0.44648801 2. 2. -0.4295595 ]
[ 2. -2.58334298 2. 2. ]
[ 2. 2. 2. 2. ]
[ 2. 2. 2. -0.07501011]]
数学和统计方法
求mean和sum
In [2]: import numpy as np
In [3]: arr = np.random.randn(5,4)
In [4]: arr
Out[4]:
array([[-0.74284535, 0.46496577, 2.32138162, 0.44785399],
[ 0.47712275, 0.83949184, -0.16869749, -0.43977791],
[-0.92417354, 1.50352369, 0.24352079, 0.38116908],
[ 0.7814867 , 0.91653392, -0.98002009, 1.13458268],
[ 0.2552531 , -0.53784857, -0.08502164, 0.86374517]])
In [5]: arr.mean()
Out[5]: 0.337612324386731
In [6]: arr.sum()
Out[6]: 6.75224648773462
arr.mean(axis=1)是“计算行的平均值”
arr.sum(0)是"计算每列的和"
In [7]: arr.mean(axis=1)
Out[7]: array([0.62283901, 0.1770348 , 0.30101 , 0.4631458 , 0.12403201])
In [8]: arr.mean(axis=0)
Out[8]: array([-0.03063127, 0.63733333, 0.26623264, 0.4775146 ])
arr.cumsum()
该函数计算累计和时,第n个元素时原矩阵中前n个元素之和,最后一个元素等于向量的总和
In [9]: arr = np.array([0,1,2,3,4,5,6,7])
In [10]: arr.cumsum()
Out[10]: array([ 0, 1, 3, 6, 10, 15, 21, 28])
多维数组时cumsum函数的使用
In [14]: arr.cumprod(axis=1)
Out[14]:
array([[ 0, 0, 0], #[0,0*1,0*1*2]
[ 3, 12, 60], #[3,3*4,3*4*5]
[ 6, 42, 336]]) #[6,6*7,6*7*8]
axis=1即跨列累乘积
axis=0即跨行累乘积
用于布尔型数组的方法
首先介绍两个方法:
any用于测试数组中是否存在一个或多个True
all用于检查数组中所有值是否都是True
这两种方法不仅适合布尔型数组,而且非布尔型数组也同样可以适用
排序
In [21]: arr = np.random.randn(5,3)
In [22]: arr
Out[22]:
array([[-1.36441297, -0.68326518, -2.21160752],
[-0.11746905, -0.19771985, -1.44681053],
[-0.11275465, -0.82776271, 1.59938679],
[ 0.35808274, 0.20359913, 0.60071386],
[ 0.80941805, 1.53926373, -0.86061444]])
In [23]: arr.sort()
In [24]: arr
Out[24]:
array([[-2.21160752, -1.36441297, -0.68326518],
[-1.44681053, -0.19771985, -0.11746905],
[-0.82776271, -0.11275465, 1.59938679],
[ 0.20359913, 0.35808274, 0.60071386],
[-0.86061444, 0.80941805, 1.53926373]])
可以看出,默认按行排序
另一个函数np.in1d用于测试一个数组中的值在另一个数组中的成员资格,返回一个布尔型数组
In [33]: values = np.array([6,0,0,3,2,5,6])
In [35]: np.in1d(values,[2,3,6]) #(in1d()中的"1"是数字)
Out[35]: array([ True, False, False, True, True, False, True])
4.4 用于数组的文件输入输出
Numpy能够读写磁盘上的文本数据或二进制数据。
np.save和np.load是读写磁盘数组数据的两个主要函数。默认情况下,数组是以未压缩的原始二进制格式在扩展名为.npy的文件中的:
In [36]: arr = np.arange(10)
In [37]: np.save('some_array',arr)
如果文件路径末尾没有扩展名.npy,则该扩展名会被自动加上。然后就可以通过np,load读取磁盘上的数组
In [38]: np.load('some_array.npy')
Out[38]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
通过np.savez可以将多个数组保存到一个未压缩文件中,将数组以关键字参数的形式传入即可
In [39]: np.savez('array_archive.npz',a = arr,b = arr)
加载.npz文件时,会得到一个类似字典的对象,该对象会对各个数组进行延迟加载
In [40]: arch = np.load('array_archive.npz')
In [41]: arch['b']
Out[41]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
如果要将数据压缩,可以使用numpy.savez_compressed:
In [42]: np.savez_compressed('arrays_compressed.npz',a = arr,b = arr)
4.5 线性代数
矩阵乘法dot函数
In [43]: x = np.array([[1.,2.,3.],[4.,5.,6.]])
In [44]: y = np.array([[6.,23.],[-1,7],[8,9]])
In [45]: x
Out[45]:
array([[1., 2., 3.],
[4., 5., 6.]])
In [46]: y
Out[46]:
array([[ 6., 23.],
[-1., 7.],
[ 8., 9.]])
In [47]: x.dot(y)
Out[47]:
array([[ 28., 64.],
[ 67., 181.]])
#x.dot(y)等价于np.dot(x,y)
In [48]: np.dot(x,y)
Out[48]:
array([[ 28., 64.],
[ 67., 181.]])
一个二维数组跟一个大小合适的一维数组的矩阵点积运算之后将会得到一个一维数组
In [49]: np.dot(x,np.ones(3))
Out[49]: array([ 6., 15.])
@符也可以用作中缀运算符,进行矩阵乘法
In [50]: x @ np.ones(3)
Out[50]: array([ 6., 15.])
numpy.random.seed()和numpy.random.RandomState()这两个在数据处理中比较常用的函数,两者实现的作用是一样的就是使每次随机生成数一样。先用Numpy的np.random.seed更改随机数生成种子
import numpy as np
np.random.seed(10)
np.random.rand(8)
array([0.77132064, 0.02075195, 0.63364823, 0.74880388, 0.49850701,
0.22479665, 0.19806286, 0.76053071])
在此基础上接着使用rand()函数得到的随机数是一样的
np.random.seed(10)
np.random.rand(8)
array([0.77132064, 0.02075195, 0.63364823, 0.74880388, 0.49850701,
0.22479665, 0.19806286, 0.76053071])
同样,numpy.random.RandomState()也做得到
import numpy as np
rng = np.random.RandomState(10)
rng.rand(8)
array([0.77132064, 0.02075195, 0.63364823, 0.74880388, 0.49850701,
0.22479665, 0.19806286, 0.76053071])
在此基础上接着使用RandomState()函数得到的随机数是一样的
rng = np.random.RandomState(10)
rng.rand(8)
array([0.77132064, 0.02075195, 0.63364823, 0.74880388, 0.49850701,
0.22479665, 0.19806286, 0.76053071])
4.7 示例:随机漫步
通过模拟随机漫步来说明如何运用数组运算。
例子:从0开始,步长1和-1出现的概率相等
我们采用内置的random模块以纯python的方式实现1000布的随机漫步
import random
import matplotlib.pyplot as plt
position = 0
walk = [position]
steps = 1000
#random.randint(0, 1)从零到一范围内随机选取整数
for i in range(steps):
step = 1 if random.randint(0, 1) else -1
position += step
walk.append(position)
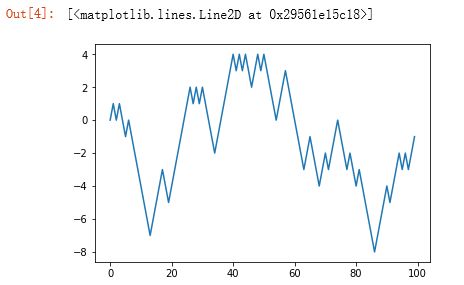
plt.plot(walk[:100])
根据前100个随机漫步生成的折线图:
用np.random模块一次性随机产生1000个“掷硬币”结果(即两个数中任选一个),将其分别设置为1或者-1,然后计算累计和
In [79]: nsteps = 1000
#
In [80]: draws = np.random.randint(0,2,size=(nwalks,nsteps))
#np.where(draws > 0,1,-1)含义:当draws>0时为1,否则为-1
In [81]: steps = np.where(draws > 0,1,-1)
#列方向上累计和
In [82]: walks = steps.cumsum(1)
In [83]: walks
Out[83]:
array([[ -1, -2, -3, ..., 4, 5, 6],
[ -1, -2, -1, ..., -62, -63, -64],
[ -1, -2, -3, ..., -54, -53, -52],
...,
[ -1, -2, -1, ..., 40, 41, 40],
[ -1, 0, -1, ..., -54, -53, -54],
[ -1, -2, -3, ..., 16, 17, 18]])
求最大值和最小值
In [84]: walks.max()
Out[84]: 122
In [85]: walks.min()
Out[85]: -105
现在假设我们想要知道本次随机漫步需要多久才能距离初始0点至少10步远(任意方向)。np.abs(walks)>=10可以得到一个布尔型数组,它表示的时距离是否达到或超过10,而我们想要知道的是第一个10或-10的索引,可以用argmax来解决这个问题,它返回的是该布尔型数组第一个最大值的索引
In [76]: (np.abs(walk) >= 10).argmax()
Out[76]: 29