在上一篇文章主要介绍了Path的基础知识,也是笔者《Android自定义控件探索之旅》系列于猪年的第一篇文章。提到猪年,想起了前不久一些著名Android公众号上推出的自定义小猪佩奇,翻看其源码后,发现这个佩奇的内部实现,实际上就用到了Path,通过点与点的链接、曲线的运用,最后绘制了一个小猪佩奇。言归正传,本篇文章是《Android自定义控件探索之旅》系列的第八篇文章,本篇文章主要介绍 Path与贝塞尔曲线的结合使用
Android自定义控件探索之旅一7
Android自定义控件探索之旅一6
Android自定义控件探索之旅一5
Android自定义控件探索之旅一4
Android自定义控件探索之旅一3
Android自定义控件探索之旅一2
Android自定义控件探索之旅一1
贝塞尔曲线的原理
关于贝塞尔曲线,笔者的这一篇文章 《必须要理解掌握的贝塞尔曲线》 对贝塞尔曲线做了详细的解释说明。由于贝赛尔曲线曲线的计算规则本质都是一样的,首先在线段上找点,这个点必须要满足等比关系,然后依次连接这些点,这些成比例的点最后连接就会形成一段光滑的曲线。那么,在Path中如何实现贝塞尔曲线?
贝塞尔曲线的实现
因此,要实现贝塞尔曲线,首先需要确认数据点,也就是曲线的起始点和结束点位置;接着,确定两点以后,还要确定曲线的弯曲程度,由于曲线的弯曲程度是由控制点来进行计算的,因此,找到控制点和曲线的起始和结束位置就可以确定贝塞尔曲线了!
贝塞尔曲线的代码实现
步骤一:
- 分析:因为它是一段光滑的曲线,直接继承View即可
- 分析:上文说到,贝塞尔曲线需要确定三个点(起始点、结束点、控制点),因此要定义6个变量(三个点,每个点有对应的 x、y)
- 分析:自定义View要用到画笔,可以在构造函数中创建画笔然后设置相应的API,这里就设置为抗锯齿属性
综上:步骤一的代码如下:
//自定义 贝塞尔曲线
public class DrawQuadToView extends View {
//贝塞尔曲线的起始点
private int startX,startY;
//贝塞尔曲线的结束点
private int endX,endY;
//贝塞尔曲线的控制点
private int eventX,eventY;
//构建画笔
Paint paint;
public DrawQuadToView(Context context) {
super(context);
init();
}
public DrawQuadToView(Context context, AttributeSet attrs) {
super(context, attrs);
init();
}
public DrawQuadToView(Context context, AttributeSet attrs, int defStyleAttr) {
super(context, attrs, defStyleAttr);
init();
}
//初始化Paint
private void init() {
paint = new Paint();
//设置抗锯齿
paint.setAntiAlias(true);
}
}
步骤二:
- 分析:因为起始点和结束点的坐标是大都是给定的,所以,确定控制点就至关重要
- 分析:控制点是不固定的,它的取值是根据用户的手指滑动进行确定的,手指滑动,就要用到onTouchEvent(MotionEvent event),通过MotionEvent.ACTION_MOVE这个事件来获取滑动的控制点属性值(也就是 x,y)
综上:步骤二的代码如下:
@Override
public boolean onTouchEvent(MotionEvent event) {
switch (event.getAction()){
case MotionEvent.ACTION_DOWN:
case MotionEvent.ACTION_MOVE:
eventX = (int) event.getX();
eventY = (int) event.getY();
invalidate();
break;
}
return true;
}
步骤三:
分析:实现贝塞尔曲线的三个点已经定义好了,现在就是三个点的赋值过程,因为赋值操作才会影响最终的效果
分析:为了方便计算,这里起始点和结束点的参考点就是屏幕的中心坐标。值得一提,onSizeChanged(int w, int h, int oldw, int oldh)这个方法非常重要,这个方法会在构造函数执行完毕后紧接着进行初始化调用,这里面的4个参数,int w, int h, int oldw, int oldh,经日志打印,w,h 代表的就是屏幕的宽高;oldw,oldh的结果是0。而且,这个方法会在控件大小发生改变时调用(因为滑动改变控制点的条件所以该方法很重要)
分析:现在三个点的赋值也确定了,现在就是onDraw(Canvas canvas)的过程,贝塞尔曲线的API是在Path中,通过Path.quadTo( )来实现的,看下Path.quadTo( )的源码:
/**
* Add a quadratic bezier from the last point, approaching control point
* (x1,y1), and ending at (x2,y2). If no moveTo() call has been made for
* this contour, the first point is automatically set to (0,0).
*
* @param x1 The x-coordinate of the control point on a quadratic curve
* @param y1 The y-coordinate of the control point on a quadratic curve
* @param x2 The x-coordinate of the end point on a quadratic curve
* @param y2 The y-coordinate of the end point on a quadratic curve
*/
public void quadTo(float x1, float y1, float x2, float y2) {
isSimplePath = false;
nQuadTo(mNativePath, x1, y1, x2, y2);
}
这个方法的英文注释翻译:从最后一点增加一个二次的贝塞尔曲线,接近控制点(x1,y1)并在(x2,y2)处结束;如果没有对这个轮廓(曲线)调用 moveTo( )方法,起始点就会自动设置成(0,0)
方法内参数对应的就是:
x1:二次曲线上控制点的x坐标
y1:二次曲线上控制点的y坐标
x2:二次曲线上结束点的x坐标
y2:二次曲线上结束点的y坐标
系统源码 明确说到:如果没有对这个轮廓(曲线)调用 moveTo( )方法,起始点就会自动设置成(0,0),所以看下 moveTo( )的源码:
/**
* Set the beginning of the next contour to the point (x,y).
*
* @param x The x-coordinate of the start of a new contour
* @param y The y-coordinate of the start of a new contour
*/
public void moveTo(float x, float y) {
nMoveTo(mNativePath, x, y);
}
这个方法的英文注释翻译:设置下一个轮廓线的起点为点(x,y)。
方法内参数对应的就是:
x:二次曲线上新轮廓的x起点坐标
y:二次曲线上新轮廓的y起点坐标
综上:步骤三的代码如下:
//值得一提的是 onSizeChanged()会在构造函数执行完毕后紧接着进行初始化
// onSizeChanged()控件大小发生改变时调用
@Override
protected void onSizeChanged(int w, int h, int oldw, int oldh) {
Log.i("info", "onSizeChanged: ");
super.onSizeChanged(w, h, oldw, oldh);
//三个点的 参考点 也就是 屏幕的中心点
centerX = w/2;
centerY = h/2;
//起始点 x、y
startX = centerX-300;
startY = centerY;
//结束点 x、y
endX = centerX + 300;
endY = centerY;
//控制点 默认是在 起始点和结束点的上面
eventX = centerX;
eventY = centerY - 250;
}
//开始绘制
@Override
protected void onDraw(Canvas canvas) {
super.onDraw(canvas);
//-------画三个点--------
paint.setColor(Color.RED);
//画起始点-红色
canvas.drawCircle(startX,startY,8,paint);
//画结束点-红色
canvas.drawCircle(endX,endY,8,paint);
paint.setColor(Color.BLUE);
//画控制点-蓝色
canvas.drawCircle(eventX,eventY,8,paint);
//-------画三个点--------
//-------画线(点连接点)--------
paint.setStrokeWidth(4);
canvas.drawLine(startX,centerY,eventX,eventY,paint);
canvas.drawLine(endX,centerY,eventX,eventY,paint);
paint.setColor(Color.GREEN);
paint.setStyle(Paint.Style.STROKE);
Path path = new Path();
//设置贝塞尔曲线的起点
path.moveTo(startX,startY);
//!!!----画二阶贝塞尔曲线!!!----
path.quadTo(eventX,eventY,endX,endY);
canvas.drawPath(path,paint);
}
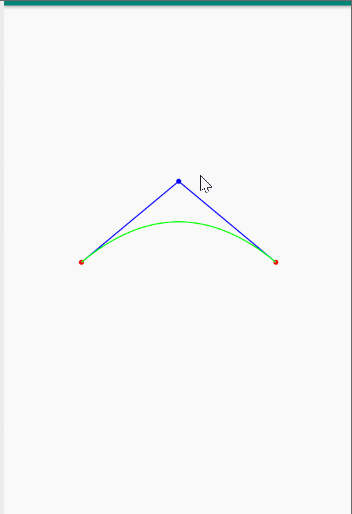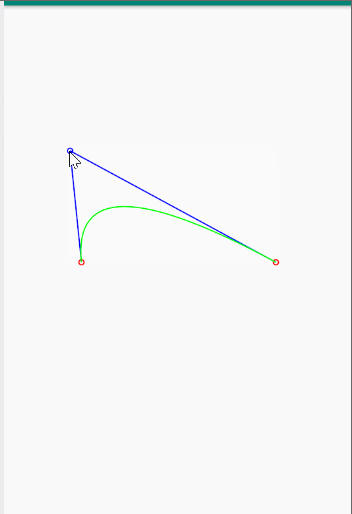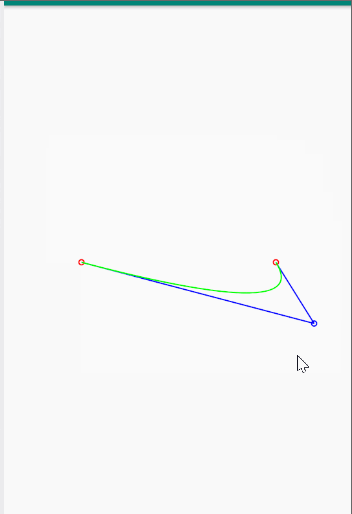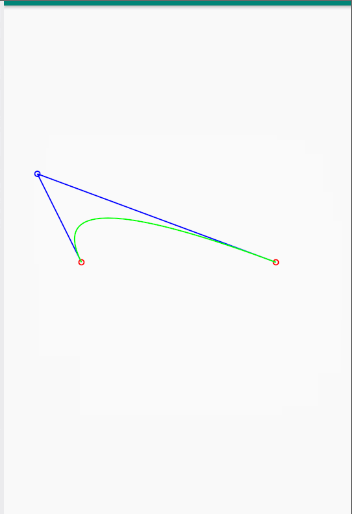
关于二次贝塞尔曲线的代码实现,大概就是这样,运行完的效果如下:
上面是二阶贝塞尔曲线的代码实现,那么三阶贝塞尔曲线该怎么实现?
贝塞尔曲线的代码实现-三阶贝塞尔
由于,三阶贝塞尔曲线是由2个控制点来进行操作的,API使用的是cubicTo(),看下系统源码:
/**
* Add a cubic bezier from the last point, approaching control points
* (x1,y1) and (x2,y2), and ending at (x3,y3). If no moveTo() call has been
* made for this contour, the first point is automatically set to (0,0).
*
* @param x1 The x-coordinate of the 1st control point on a cubic curve
* @param y1 The y-coordinate of the 1st control point on a cubic curve
* @param x2 The x-coordinate of the 2nd control point on a cubic curve
* @param y2 The y-coordinate of the 2nd control point on a cubic curve
* @param x3 The x-coordinate of the end point on a cubic curve
* @param y3 The y-coordinate of the end point on a cubic curve
*/
public void cubicTo(float x1, float y1, float x2, float y2,
float x3, float y3) {
isSimplePath = false;
nCubicTo(mNativePath, x1, y1, x2, y2, x3, y3);
}
这段源码跟quadTo()几乎是一样的,就是多了一个控制点,这里就不做试验了。
如果这篇文章对您有开发or学习上的些许帮助,希望各位看官留下宝贵的star,谢谢。
Ps:著作权归作者所有,转载请注明作者, 商业转载请联系作者获得授权,非商业转载请注明出处(开头或结尾请添加转载出处,添加原文url地址),文章请勿滥用,也希望大家尊重笔者的劳动成果