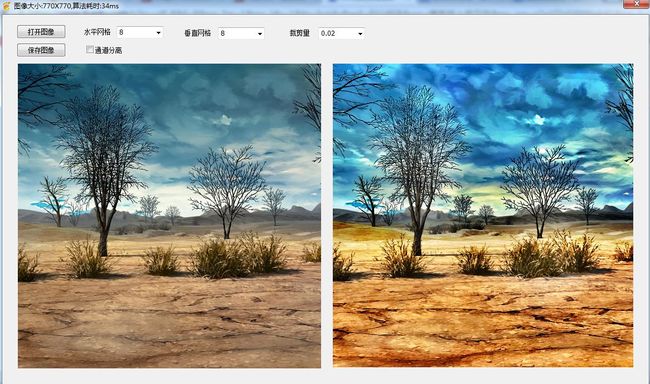
直方图均衡化(HE)是一种很常用的直方图类方法,基本思想是通过图像的灰度分布直方图确定一条映射曲线,用来对图像进行灰度变换,以达到提高图像 对比度的目的。该映射曲线其实就是图像的累计分布直方图(CDF)(严格来说是呈正比例关系)。然而HE是对图像全局进行调整的方法,不能有效地提高局部 对比度,而且某些场合效果会非常差。如:
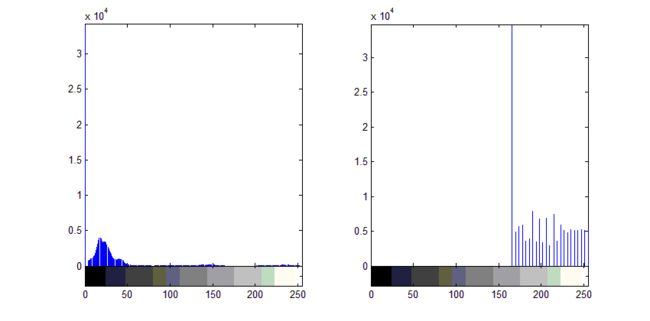
上述原图和HE结果图的直方图分别为:
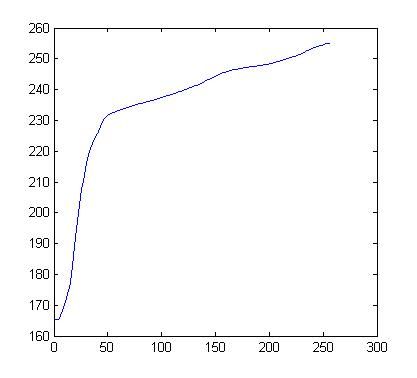
因为从原图的直方图中求取的映射函数(CDF)形状为:
将它作用于原图像会导致直方图被整体右移,没有充分利用整个灰度动态范围。
为了提高图像的局部对比度,有人提出将图像分成若干子块,对子块进行HE处理,这便是AHE(自适应直方图均衡化),使用AHE处理上图得到:
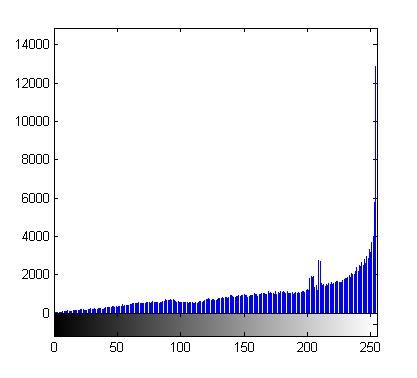
结果直方图:
可 以看出结果图像的灰度较好地分布在了全部动态范围上。从结果图像上也可以看出,局部对比度的确得到了提高,视觉效果要优于HE。但是仍然有个问题:AHE 对局部对比度提高过大,导致图像失真。看看背景区,本来的黑色背景现在已经变成白色了,原因是因为背景区中的局部子块统计得到的直方图在0灰度处幅值太高 (实际上全黑子图基本上就集中在0灰度处),这样导致映射曲线斜率过高,将所有灰度值都映射到整个灰度轴的右侧,所以结果图中背景偏白(另外局部对比度过 高还会放大图像中的噪声,不过上图并没有体现这一点)。
为了解决这个问题,我们必须对局部对比度进行限制,这就是我们今天的主题:CLAHE。
从HE中我们知道,映射曲线T与CDF关系为:(M为最高灰度值,N为像素个数)
限制对比度,其实就是限制CDF的斜率,又因累计分布直方图CDF是灰度直方图Hist的积分:
反过来:
也就是说限制CDF的斜率就相当于限制Hist的幅度。
因此我们需要对子块中统计得到的直方图进行裁剪,使其幅值低于某个上限,当然裁剪掉的部分又不能扔掉,我们还需要将这部分裁剪值均匀地分布在整个灰度区间上,以保证直方图总面积不变,如下图:
可以看到,这时直方图又会整体上升了一个高度,貌似会超过我们设置的上限。其实在具体实现的时候有很多解决方法,你可以多重复几次裁剪过程,使得上升的部分变得微不足道,或是用另一种常用的方法:
设 裁剪值为ClipLimit,求直方图中高于该值的部分的和totalExcess,此时假设将totalExcess均分给所有灰度级, 求出这样导致的直方图整体上升的高度L=totalExcess/N,以upper= ClipLimit-L为界限对直方图进行如下处理:
(1)若幅值高于ClipLimit,直接置为ClipLimit;
(2)若幅值处于Upper和ClipLimit之间,将其填补至ClipLimit;
(3)若幅值低于Upper,直接填补L个像素点;
经过上述操作,用来填补的像素点个数通常会略小于totalExcess,也就是还有一些剩余的像素点没分出去,这个剩余来自于(1)(2)两处。这时我们可以再把这些点均匀地分给那些目前幅值仍然小于ClipLimit的灰度值。
这里给出一段代码:(摘自Matlab的adapthisteq.m),描述的就是上述过程:
% total number of pixels overflowing clip limit in each bin totalExcess = sum(max(imgHist - clipLimit,0)); % clip the histogram and redistribute the excess pixels in each bin avgBinIncr = floor(totalExcess/numBins); upperLimit = clipLimit - avgBinIncr; % bins larger than this will be % set to clipLimit % this loop should speed up the operation by putting multiple pixels % into the "obvious" places first for k=1:numBins if imgHist(k) > clipLimit imgHist(k) = clipLimit; else if imgHist(k) > upperLimit % high bin count totalExcess = totalExcess - (clipLimit - imgHist(k)); imgHist(k) = clipLimit; else totalExcess = totalExcess - avgBinIncr; imgHist(k) = imgHist(k) + avgBinIncr; end end end % this loops redistributes the remaining pixels, one pixel at a time k = 1; while (totalExcess ~= 0) %keep increasing the step as fewer and fewer pixels remain for %the redistribution (spread them evenly) stepSize = max(floor(numBins/totalExcess),1); for m=k:stepSize:numBins if imgHist(m) < clipLimit imgHist(m) = imgHist(m)+1; totalExcess = totalExcess - 1; %reduce excess if totalExcess == 0 break; end end end k = k+1; %prevent from always placing the pixels in bin #1 if k > numBins % start over if numBins was reached k = 1; end end
CLAHE和AHE中另一个重要的问题:插值。
将图像进行分块处理,若每块中的像素点仅通过该块中的映射函数进行变换,则会导致最终图像呈块状效应:
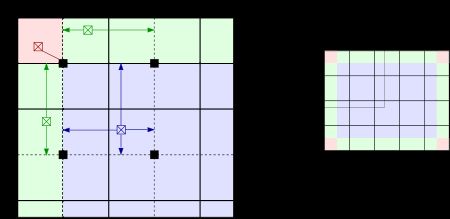
为了解决这个问题,我们需要利用插值运算,也就是每个像素点出的值由它周围4个子块的映射函数值进行双线性插值得到,如下图:
上图中,为了求蓝色像素点处的值,需要利用它周围四个子块的映射函数分别做变换得到四个映射值,再对这四个值做双线性插值即可。
当 然对于边界处的像素点则不是通过四个子块进行插值,如上图红色像素点直接以一个子块的映射函数做变换,绿色像素则以两个子块做映射函数做线性插值。这里讲 的边界处像素是指落在图像左上角,左下角、右上角,右下角的四个子块中心像素点围成的四边形之外的像素。如下图,将图像分为8x8子块,边界像素即落在灰 色区域的像素点。
利用插值对图像进行处理的整体架构如下:
for (Y = 0; Y <= TileY; Y++) //TileY为Y方向网格数 { if (Y == 0) { SubY = TileYDim >> 1; YU = 0; YB = 0; } else if (Y == TileY) { SubY = TileYDim >> 1; YU = TileY-1; YB = YU; } else { SubY = TileYDim; YU = Y - 1; YB = Y; } for (X = 0; X <= TileX; X++) //TileX为X方向网格数 { if (X == 0) { SubX = TileXDim >> 1; XL = 0; XR = 0; } else if (X == TileX) { SubX = TileXDim >> 1; XL = TileX - 1; XR = XL; } else { SubX = TileXDim; XL = X - 1; XR = X; } MapLU = &pMapArray[numBins * (YU * TileX + XL)];//左上角映射函数 MapRU = &pMapArray[numBins * (YU * TileX + XR)];//右上角映射函数 MapLB = &pMapArray[numBins * (YB * TileX + XL)];//左下角映射函数 MapRB = &pMapArray[numBins * (YB * TileX + XR)];//右下角映射函数 Interpolate(pImPointer,Stride,Channel,MapLU,MapRU,MapLB,MapRB,SubX,SubY,aLUT);//插值 pImPointer += SubX; } pImPointer+=(SubY-1)*Stride; }
注意的是,上述循环需要(TileX+1)*(TileY+1)次,而不是TileX*TileY次。,原因很简单,以X方向为例,两侧边界处的半宽子块(灰色区)也各需要处理一次,如下图:
通过双线性插值可以基本消除块状效应:
对 于彩色图像,三通处理分开处理会导致严重的偏色,故我们可以将其进行颜色空间转换(如RGB转为HSV),然后仅对亮度分量处理,再反变换回RGB空间。 不过网上有高手将R、G、B统一处理[2](也就相当于把一个像素点拆成三个像素点),这样得到的效果也不错,而且省去了颜色空间转换的时间,我们这里也 仿照他来吧:
另外,CLAHE对雾天图像处理效果也不错:
至于编程,我基本就是翻译adaphisteq.m,另外还有一些参考资源:CLAHE代码(MATLAB)
这里给出编译好的文件,有兴趣的朋友可以下载看看:ImageProcess(CLAHE)
参考:
[1]https://en.wikipedia.org/wiki/Adaptive_histogram_equalization
[2]http://www.cnblogs.com/Imageshop/archive/2013/04/07/3006334.html