编译原理第三次作业

1.已知文法：

S->a|^|(T)

T->T,S|S

分析句型（T,(^,a))，求全部的短语、直接短语和句柄。

解：

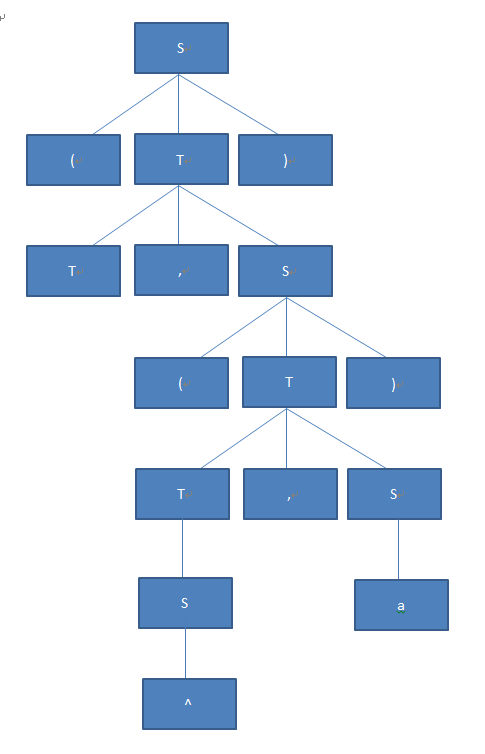
S-> (T) -> (T,S) -> (T,(T)) -> (T,(T,S)) -> (T,(S,S)) –> (T,(^,S)) -> (T,(^,a))

   

 

 

由上述树可知

该句型的短语有：^   a   ^,a   (^,a)   T, (^,a)  (T, (^,a))

该句型的直接短语有：^   a

该句型的句柄为：^

 

 

2.   构造上下文无关文法，描述语言：

 

｛aⁿbⁿ|n>=0｝

｛a^mbⁿ|m>=n>=0｝

｛(ab)ⁿ|n>=0｝

｛a^mbⁿ|m,n>=1｝ 

 

解：

(1)

｛aⁿbⁿ|n>=0｝：

S-> aSb | ab | ε

(2)

｛a^mbⁿ|m>=n>=0｝：

S -> aSb | ab   |  a | ε

(3)

｛(ab)ⁿ|n>=0｝

S->(ab)S | (ab)| ε

｛a^mbⁿ|m,n>=1｝

       S-> aS | Sb | ab 

 

 

3.如果if语句的方法：

stmt->if expr then stmt

     | if expr then stmt else stmt

     | other

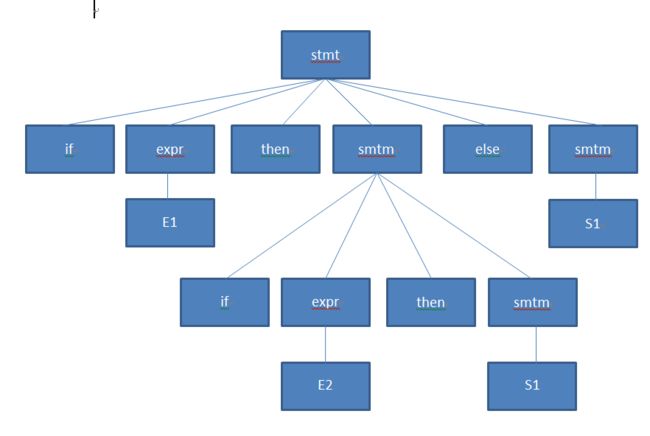
句子if E1 then if E2 then S1 else S2是否有两棵不同的语法树？说明了什么？

 

答：有题可知该题有2种语法树

树1

 

 

有树2 

 

因为语法树有2种，故该语句具有二义性