本章涉及知识点:
1、时间序列分析
2、平稳时间序列
3、白噪声
4、AR自回归模型
5、MA滑动平均模型
6、ARMA模型
7、ARIMA模型
8、差分计算
9、相关性分析—协方差
10、相关性分析—Pearson相关系数
11、时间序列相关性分析—ACK和PACK
12、AIC和BIC准则
13、一阶自相关检验—DW检验
14、ARIMA模型的步骤
15、ARIMA模型实战案例
一、时间序列分析
时间序列:在一段时间T内,按照时间顺序测量某个随机变量的取值序列。即
区别于一般的时间函数为
其中自变量是时间t,表示在f的作用法则下,将自变量t映射为因变量y
而时间序列函数为
其中自变量是Xt的前p个序列值,表示在f的作用法则下,将自变量Xt的前p个序列值映射为因变量Xt
综上分析可知
(1)对于单值函数f(t),关心的是时间t和实值y的映射关系
(2)对于时间序列Xt,关心的是Xt的前p个序列值和Xt的映射关系
二、平稳时间序列
独立时间序列:对于{}均彼此独立,即任意都不含有的信息
稳定时间序列:的信息隐含在其历史{}之中
我们需要由历史来推测未来,则研究的序列对象是稳定时间序列,其必须满足:
(1)
(2)
(3)
即稳定时间序列满足:常量的均值、常量的方差、与时间t无关的自协方差
且对于任意序列和,共同平移k步后的序列得到的序列和具有相同的协方差,即
上式称为协方差结构的平移不变性
对于平稳序列的任意n阶自协方差矩阵
任意取一个n维向量a,则
则证明平稳序列的任意n阶自协方差矩阵是非负定矩阵
三、白噪声
白噪声服从高斯分布,记时间序列对于任意i和j,如果满足
则时间序列是一个白噪声,记为。
我们一般用白噪声来验证原始时间序列和拟合时间序列的残差序列
即原始时间序列为,拟合时间序列为,则残差序列为:
当近似的满足白噪声,则时间序列模型很好的捕捉了自相关性
例如:对于随机变量U1,U2,...独立分布且都在(0,2pi)上均匀分布,假设时间序列为:
则分别计算和,得
则时间序列是独立的正态白噪声
四、AR自回归模型
对于任意一个稳定时间序列,当满足如下关系:
为一个p阶的自回归模型,记为模型
模型的意义为:
(1)任意一个t时刻的序列值 = t时刻的前p个序列值的线性组合 + t时刻的随机误差
(2)以历史序列为自变量,建立线性模型来预测未来
五、MA滑动平均模型
对于任意一个稳定时间序列,由AR模型得到自回归系数的估计为
记是的残差序列,即
则当满足如下关系:
为一个q阶的滑动平均模型,记为模型,其中满足白噪声
模型的含义为:
(1)任意一个t时刻的序列值 = t时刻的前q个序列的白噪声累加和的线性组合 + t时刻的随机误差
(2)以历史白噪声为自变量,建立线性模型来预测未来
六、ARMA模型
将一个p阶的自回归模型和一个q阶的滑动平均模型组合在一起,便得到了一个阶数为(p,q)的自回归滑动平均模型,记为模型,即
模型的意义为:
(1)将AR和MA模型的优势线性互补起来
(2)以历史序列和历史白噪声序列为自变量,建立线性模型来预测未来
七、ARIMA模型
ARIMA模型:对时间序列进行d次差分得到一个新的差分时间序列,再对该序列使用ARMA模型,为此ARIMA模型比ARMA模型多了一层思想:差分
八、差分计算
对于任意一个时间序列进行d次差分,设是t时刻的差分值
当d=0时,
当d=1时,
当d=2时,
一般的,一个非平稳序列经过d次差分后,可以转化为平稳时间序列
九、相关性分析—协方差
假设两个随机变量X和Y满足未知的概率分布,则我们可以使用协方差来衡量X和Y之间的相关性
而在实际应用中,由于整体的概率分布未知(无法计算出数学期望),则用X和Y的观测值来计算样本的协方差,其中和分别为X和Y的均值
当,X和Y正相关,有相同的变化趋势
当,X和Y负相关,有相反的变化趋势
当,X和Y没有线性关系
用协方差描述随机变量的相关性,只能做到定性分析,无法做到定量分析,比如:一组身高和体重的协方差为205.6,这个数值是一个正数,只能说明身高体重具有正相关型,而并没有给出其相关性大小的判断标准。
因此协方差具有量纲效应
十、相关性分析—Pearson相关系数
为了对随机变量的相关性做定量分析,需要消除协方差之间的量纲,为此引入Pearson相关系数
通过X和Y的标准差来归一化X和Y的协方差,且
当,X和Y正相关
当,X和Y负相关
当,X和Y没有线性关系
当,X和Y具有一定程度的线性关系
十一、时间序列相关性分析—ACK和PACK
由于时间序列的自变量是一维的,则使用Pearson相关系数判断其相关性时,需要找到除自身序列值外的一个变量与之比较关系,为此时间序列有如下特点:
时间序列只能比较自己和自己滞后的序列值,即形成自相关关系
ACK自相关系数:度量变量过去的行为对变量现在的影响,即
ACK表示:历史序列和当前序列之间的相关性
PACK偏自相关系数:计算某一个变量对另一个变量的相关程度时,把其他变量视为常数
PACK表示:计算时间序列对的相关性影响,需要排除k-1个()中间变量的影响
十二、AIC和BIC准则
AIC和BIC准则可以辅助量化ARMA模型的定阶,通过最小化AIC和BIC指标来搜索出模型的最优阶数p和q
AIC准则:全称是最小化信息量准则,定义为
其中k为模型的阶数,L为模型的极大似然函数
AIC准则有一定的缺陷:即样本容量很大时,k的惩罚因子一直是常数2,与样本容量没有关系,这样会导致AIC增大
BIC准则:全称是贝叶斯信息准则,定义为
其中n为样本容量
BIC很好的弥补了AIC的不足,将样本容量n关联到k的惩罚因子中
十三、一阶自相关检验—DW检验
由ACK的定义
我们设,,则构造统计量DW为:
分析DW,当n非常大时,有,则
DW检验有以下特点:
(1)DW检验仅适用于一阶自相关的检验
(2)如果不存在一阶自相关,一般也不存在高阶序列相关
(3)实际应用中,对于序列相关问题一般只进行DW检验
由ACK(1)的取值来决定DW的取值情况:
当ACK(1)=1,说明相关变量组存在一阶正相关,DW=0
当ACK(1)=-1,说明相关变量组存在一阶负相关,DW=4
当ACK(1)=0,说明相关变量组完全不相关,DW=2
十四、ARIMA模型的步骤
通过上述知识点,我们可以归纳出ARIMA模型的步骤为:
(1)获取观测的时间序列,检验序列的平稳性
(2)缩小序列值域,一般取对数序列
(3)对于非平稳序列,通过d次差分运算转化为稳定序列
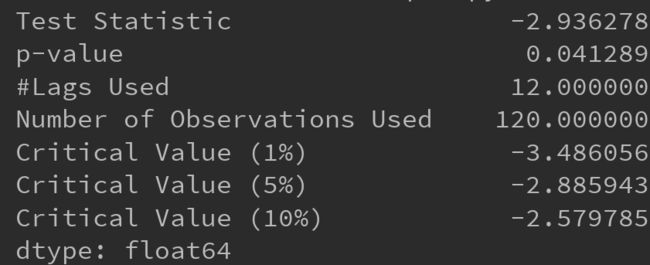
(4)ADF单根检验,观察p-value值是否小于5%
(5)模型定阶:对平稳时间序列分别求自相关系数ACF和偏自相关系数PACF,通过AIC、BIC准则得到最佳的阶数p和q
(6)模型训练:通过(p,d,q)阶数训练ARIMA模型,学习到残差序列
(7)模型检验:残差序列是否满足白噪声、DW检验一阶自相关性、观察残差序列拟合原始残差序列效果
(8)模型测试:残差序列逆向还原拟合时间序列,残差序列交叉验证测试集
十五、ARIMA模型实战案例
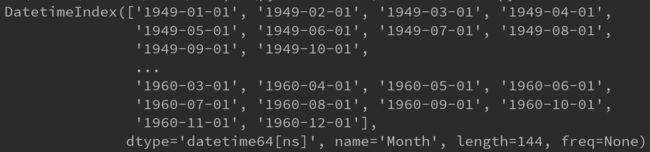
setp1:获取时间序列样本集
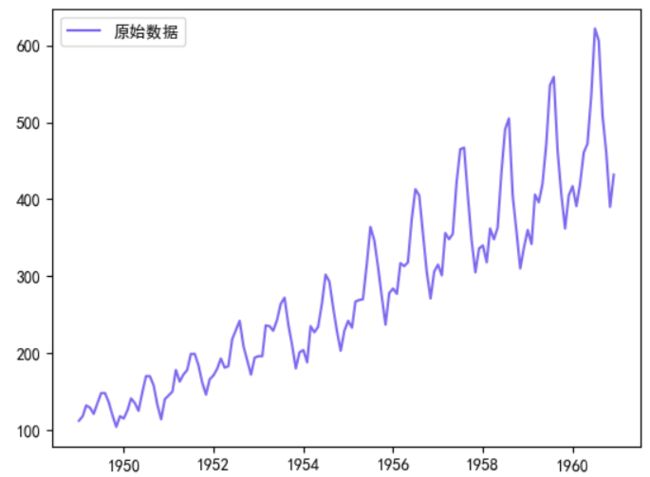
样本数据为1949年1月到1960年12月每月的乘客数量
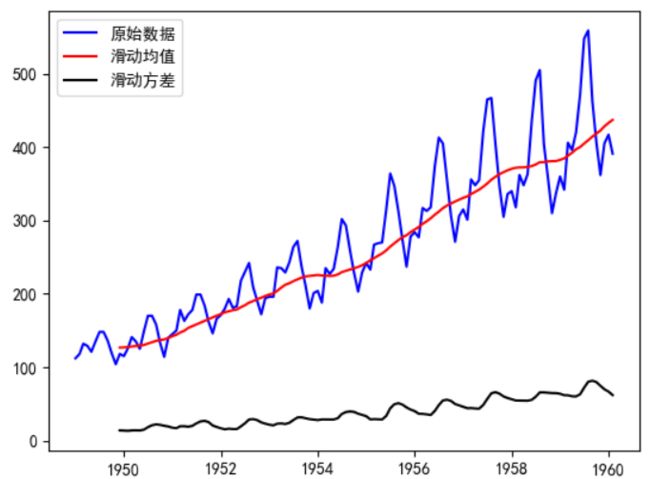
我们通过原始序列的滑动均值和方差,观察其稳定性
可以看到原始序列的滑动均值/方差都有逐渐增大的趋势,该序列不稳定
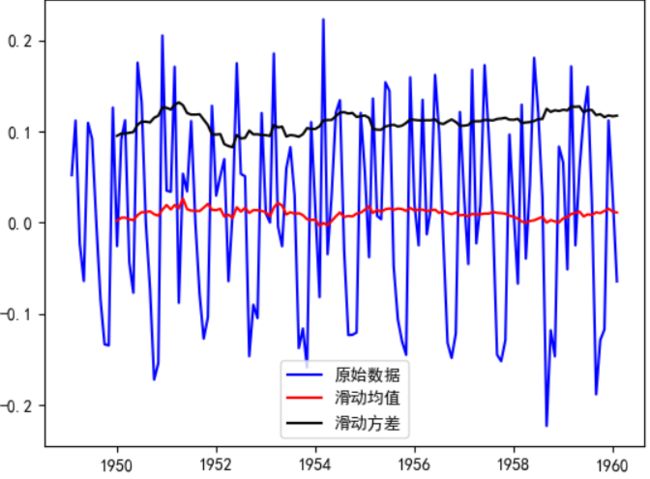
setp2:取对数和一阶差分,通过滑动均值和方差、以及ADF单根检验差分序列是否满足稳定性
可以看到,差分后滑动均值/方差逐渐趋于平稳,P值小于5%,差分序列是稳定的
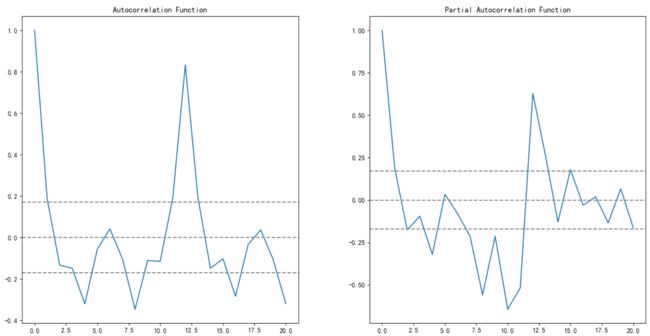
setp3:模型定阶,画出ACF和PACF的图像
上下两条灰线之间是置信区间
非统计学专业出身,肉眼定阶法缺乏经验。所以在阶数和数据量不大的场景下,可以选择暴力定阶法,通过遍历可能的阶数,计算ACK和PACK对应于AIC和BIC准则下的最小值,作为最优阶数p和q的参考
上述选出基于BIC准则下最优参数(p,q)=(10,7)
setp4:训练ARIMA模型,即ARIMA(10,1,7),得到模型和残差序列
setp5:检验模型学习效果
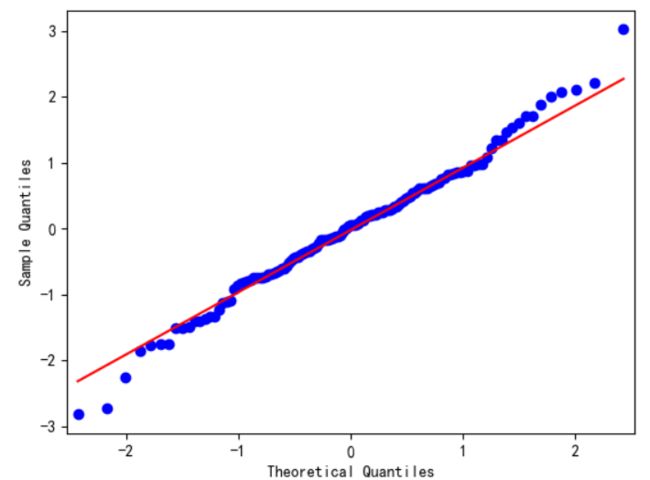
(1)残差序列是否满足白噪声—qq图
qq图的x轴表示正态分布分位数,y轴为样本分位数,可以看到残差序列基本位于一条直线上,即满足白噪声
(2)DW检测一阶相关性
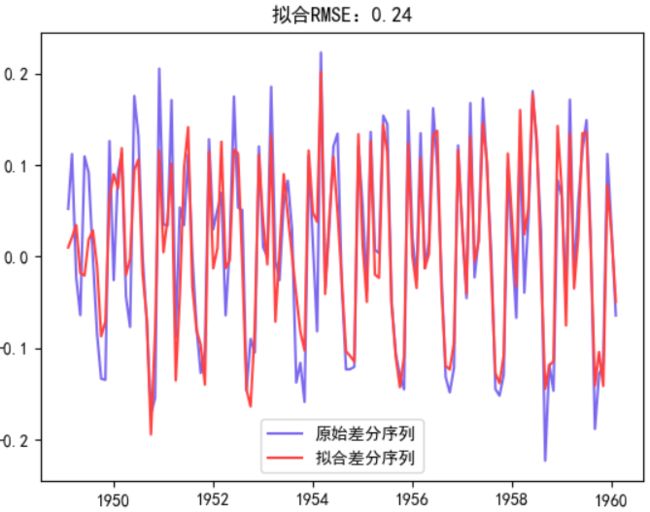
(3)观察学习到的差分序列拟合效果
setp6:模型测试效果
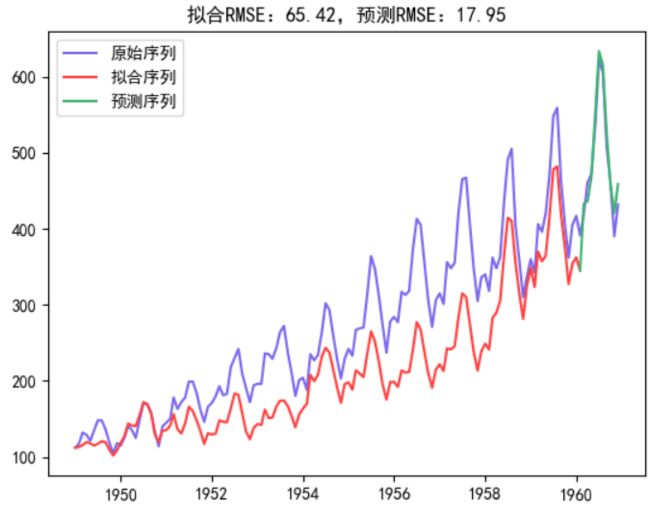
(1)残差序列逆向还原拟合时间序列
(2)残差序列交叉验证测试集
实验结果可以看到,随着时间的推移,模型的拟合效果和预测效果较为理想
案例代码见:时间序列模型:ARIMA