常用算法学习笔记

写在前面

上学时的数学课会介绍很多定理、公式，但是少有介绍在日常生活中运用的案例。任何一个设计模式、算法都应该是从生活中来，又可以回到生活中去。最近一直在做异常检测与故障诊断相关的事情，越来越觉得算法的重要性，这里记录一下，最近学习的一些常用算法与应用场景。尽量描述的短小、通俗。

大O表示法的理解

大O表示法指出了算法在最坏情况下的运行时间。
几种常见的算法运行时间如下：

• O(logn)，也叫对数时间，这样的算法包括二分查找。
• O(n)，也叫线性时间，这样的算法包括简单查找。
• O(n*logn)，这样的算法包括第4章将介绍的快速排序——一种速度较快的排序算法。
• O(n^2 )，这样的算法包括第2章将介绍的选择排序——一种速度较慢的排序算法。
• O(n!)，这样的算法包括接下来将介绍的旅行商问题的解决方案——一种非常慢的算法。

image

主要启示：

• 算法的速度指的并非时间，而是操作数的增速。
• 谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。
• 算法的运行时间用大O表示法表示。
• O(logn)比O(n)快，当需要搜索的元素越多时，前者比后者快得越多。

查找的前提-排序

日常生活中，我们会有大量的场景去查找东西，比如：查字典，查电话簿，查商品。如果查询的数据集可以以某种形式进行排序，在有序的数据集中进行查找，将大大提高我们的查询速度，人是这样，计算机同样是这样。
排序相关的数据结构-数组与链表的特点：

• 链表的元素是分开的，其中每个元素都存储了下一个元素的地址。
• 数组的读取速度很快。
• 链表的插入和删除速度很快。

选择排序

场景：老师给班级学生的英语成绩进行排序。最直观的排序方式是，每次在原始集合中找出最大的，然后放到新集合中，依次将原始集合中的数据都遍历一遍。它的算法运行时间为O(n^2).
事例代码在这里

快排的前提-递归

递归指的是调用自己的函数，递归操作被广泛的使用在很多算法中，它是我们高中数学中归纳证明在计算机中的应用。递归很可能性能没有多写几个循环来的高，但是它使我们的程序通俗易懂，我们需要在两者之间取得一个平衡。在使用递归时，需要特别注意基线条件：退出递归的条件。计算机在调用函数时都会使用栈这个数据结构，每当你调用函数时，计算机都像这样将函数调用涉及的所有变量的值存储到内存中。如果基线条件没有控制好，很容易造成栈溢出。

在使用递归时，你可能看不到循环操作，其实对栈的后进先出(LIFO)操作隐藏了一个循环操作。存储详尽的信息可能占用大量的内存。每个函数调用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。在这种情况下，你有两种选择:

• 重新编写代码，转而使用循环。
• 使用尾递归。而并非所有的语言都支持尾递归。

快速排序

快速排序是远快于选择排序的排序方式，它使用到了递归，基线条件是数组为空或只包含一个元素。在这种情况下，只需原样返回数组，不用排序。快速排序需要经历下面的步骤：

• 选择基准值。
• 将数组分成两个子数组：小于基准值的元素和大于基准值的元素。
• 对这两个子数组进行排序。

Java8代码事例如下：

private static List quicksort(List list) {
    if (list.size() < 2) {
        //基线条件：为空或只包含一个元素的数组是“有序”的
        return list;
    } else {
        //递归条件
        Integer pivot = list.get(0);

        //由所有小于基准值的元素组成的子数组
        List less = list.stream().skip(1).filter(el -> el <= pivot)
                .collect(Collectors.toList());

        //由所有大于基准值的元素组成的子数组
        List greater = list.stream().skip(1).filter(el -> el > pivot)
                .collect(Collectors.toList());

            // 合并三个分区形成新的排序后的数组
        return Stream.of(
                quicksort(less).stream(),
                Stream.of(pivot),
                quicksort(greater).stream())
                .flatMap(Function.identity()).collect(Collectors.toList());
    }
}

面试的时候， 还经常会让手写快速排序算法。

简单查找、二分查找

简单查找与之前说的选择排序，都是最容易想到的处理方式，但是算法运行时间很高为O(n)，傻傻的查找。二分查找，在进行排序的前提下，每次取集合中的中值与目标值进行比较，很快就可以定位目标，其算法运行时间为O(logn).

Java8代码事例如下：

// 二分查找前提是被查找集合是排序过的
private static Integer binarySearch(int[] list, int item) {
    int low = 0;
    int high = list.length - 1;

    while (low <= high) {//只要范围没有缩小到只包含一个元素
        int mid = (low + high) / 2; //检查中间元素
        int guess = list[mid];
        if (guess == item) { // 找到了元素
            return mid;
        }
        if (guess > item) { // 猜的大了
            high = mid - 1;
        } else { // 猜的小了
            low = mid + 1;
        }
    }
     // 没有指定元素
    return null;
}

散列表可以帮我们提升算法运行效率

散列表中最重要的是散列函数，散列函数将所有的键都映射到一个位置，而最理想的情况是，散列函数将键均匀地映射到散列表的不同位置，如果散列表存储的链表很长，散列表的速度将急剧下降。散列表是数组与链表两种数据结构的结合体，链表用来解决哈希冲突时的数据存储。然而，如果使用的散列函数很好，这些链表就不会很长！

散列表的查找速度与数组一样快，而插入和删除速度与链表一样快，因此它兼具两者的优点！但在最糟情况下，散列表的各种操作的速度都很慢。因此，在使用散列表时，避开最糟情况至关重要。为此，需要避免冲突。而要避免冲突，需要有：

• 较低的填装因子；
• 良好的散列函数。
  填装因子越低，发生冲突的可能性越小，散列表的性能越高。一个不错的经验规则是：一旦填装因子大于0.7，就调整散列表的长度。

散列表适合用于模拟映射关系。散列表可用于缓存数据（例如，在Web服务器上）。散列表非常适合用于防止重复。这些都将大大提高使用散列表的算法的速度。

SHA算法

SHA算法可以帮助我们做类似下面的事情：

• 可以快速帮你比较两个文件是否相同。
• 文件是否有被修改过。
• 在不记录用户真实密码的前提下完成登录身份验证。

局部敏感散列算法SimHash

如果你对字符串做细微的修改，Simhash生成的散列值也只存在细微的差别。这让你能够通过比较散列值来判断两个字符串的相似程度，可以做下面的应用：

• 使用Simhash来判断网页是否已搜集。
• 老师可以使用Simhash来判断学生的论文是否是从网上抄的。
• 允许用户上传文档或图书，以便与人分享，但不希望用户上传有版权的内容！可使用SimHash来检查上传的内容是否有类似的，如果类似，自动拒绝。

广度优先搜索算法

使用广度优先搜索帮助你完成下面的一些事情：

• 编写国际跳棋AI，计算最少走多少步就可获胜；
• 编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如将READED改为READER需要编辑一个地方；
• 根据你的人际关系网络找到关系最近的医生。

它是对复杂关系网的计算分析，而需要注意的是这些关系网中每一个关系没有权重，如果关系有权重可能需要使用其他算法。关系网在数学上对应着图。

image

广度优先搜索可回答两类问题：

• 第一类问题：从节点A出发，有前往节点E的路径吗？（在你的人际关系网中，有芒果销售商吗？）
• 第二类问题：从节点A出发，前往节点E的哪条路径最短？（哪个芒果销售商与你的关系最近？）

实现该算法的关键点是使用散列表记录关系图，使用队列(先进先出FIFO)记录需要遍历的节点，使用数组记录哪些节点是否被遍历过，避免进入死循环。

Java8代码事例：
查找和你关系最近的名字以m结尾的人。

import java.util.*;

public class BreadthFirstSearch {
    private static Map> graph = new HashMap<>();

    private static boolean search(String name) {
        Queue searchQueue = new ArrayDeque<>(graph.get(name));
        // 该队列记录已经被存储的
        List searched = new ArrayList<>();

        while (!searchQueue.isEmpty()) {
            String person = searchQueue.poll();
            // Only search this person if you haven't already searched them
            if (!searched.contains(person)) {
                if (person_is_seller(person)) {
                    System.out.println(person + " is right!");
                } else {
                    searchQueue.addAll(graph.get(person));
                    // 标记已经检索过
                    searched.add(person);
                }
            }
        }

        return false;
    }

    private static boolean person_is_seller(String name) {
        return name.endsWith("m");
    }

    public static void main(String[] args) {
        graph.put("you", Arrays.asList("alice", "bob", "claire"));
        graph.put("bob", Arrays.asList("anuj", "peggy"));
        graph.put("alice", Arrays.asList("peggy"));
        graph.put("claire", Arrays.asList("thom", "jonny"));
        graph.put("anuj", Collections.emptyList());
        graph.put("peggy", Collections.emptyList());
        graph.put("thom", Collections.emptyList());
        graph.put("jonny", Collections.emptyList());

        search("you");
    }
}

狄克斯特拉算法

使用狄克斯特拉算法可以帮助我们完成下面的一些事情：

• 给外卖小哥规划时间最短的取餐、送餐路径。

它与广度优先搜索算法不同的是，计算的关系网中， 每一个关系都有权重。图中的环可能导致该算法失效。
狄克斯特拉算法只适用于有向无环图（directed acyclic graph，DAG）。

image

算法需要三个散列表分别记录：

• 散列表graph，记录整个有向无环图的关系与权重。
• 散列表costs，记录从起点到各个节点的权重开销，这个散列表需要实时更新。
• 散列表parent，记录与起点关联的节点的父结点，这个散列表需要实时更新。

image

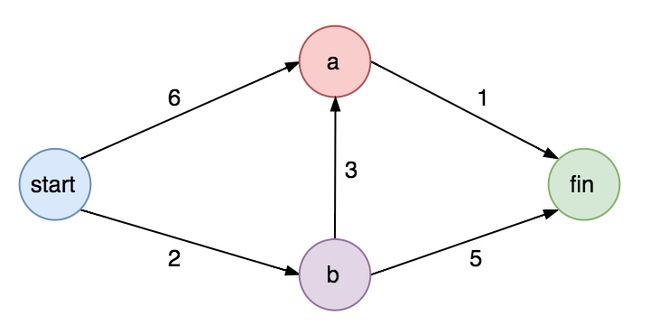
根据上图下面是一个Java8的代码事例：

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

public class DijkstrasAlgorithm {
    //整个存储有向无环图数据
    private static Map> graph = new HashMap<>();
    //存储已经处理过的节点
    private static List processed = new ArrayList<>();

    // 找出开销最小的节点，节点的开销指的是从起点出发前往该节点需要多长时间
    private static String findLowestCostNode(Map costs) {
        Double lowestCost = Double.POSITIVE_INFINITY; //初始值设置为无穷大
        String lowestCostNode = null;

        // 遍历所有节点
        for (Map.Entry node : costs.entrySet()) {
            Double cost = node.getValue();
            // 如果当前节点开销更低，并且没有被处理过，将其设为开销最低。
            if (cost < lowestCost && !processed.contains(node.getKey())) {
                // ... set it as the new lowest-cost node.
                lowestCost = cost; 
                lowestCostNode = node.getKey();
            }
        }
        return lowestCostNode;
    }

    public static void main(String[] args) {
        //根据上图构建整个数据集
        graph.put("start", new HashMap<>());
        graph.get("start").put("a", 6.0);
        graph.get("start").put("b", 2.0);

        graph.put("a", new HashMap<>());
        graph.get("a").put("fin", 1.0);

        graph.put("b", new HashMap<>());
        graph.get("b").put("a", 3.0);
        graph.get("b").put("fin", 5.0);

        graph.put("fin", new HashMap<>());

        // 初始用来存储从起点开始的相邻节点的所有开销
        Map costs = new HashMap<>();
        costs.put("a", 6.0);
        costs.put("b", 2.0);
        //不是相邻的暂时设为无穷大
        costs.put("fin", Double.POSITIVE_INFINITY);

        // 初始用来存储从起点开始的相邻节点的所有父结点
        Map parents = new HashMap<>();
        parents.put("a", "start");
        parents.put("b", "start");
        //不是相邻的暂时设为null
        parents.put("fin", null);

        // 在未处理的节点中找出开销最小的节点
        String node = findLowestCostNode(costs);
        //这个循环在所有节点都被处理过后结束
        while (node != null) {
            Double cost = costs.get(node);
            Map neighbors = graph.get(node);
            //遍历当前节点的所有邻居
            for (String n : neighbors.keySet()) {
                double newCost = cost + neighbors.get(n);
                // 如果经当前节点前往该邻居开销更低
                if (costs.get(n) > newCost) {
                    // 更新该邻居的开销
                    costs.put(n, newCost);
                    // 同时将该邻居的父结点设为当前节点
                    parents.put(n, node);
                }
            }
            // 将当前节点标记处理过
            processed.add(node);

            // 去找下一个需要处理的节点，并循环
            node = findLowestCostNode(costs);
        }

        System.out.println("Cost from the start to each node:");
        System.out.println(costs); // { b: 2,a: 5, fin: 6 }
    }
}

动态规划

什么场景下使用动态规划：

• 需要在给定约束条件下优化某种指标时，动态规划很有用。
• 问题可分解为离散子问题时，可使用动态规划来解决。
• 每种动态规划解决方案都涉及网格。
• 单元格中的值通常就是你要优化的值。
• 每个单元格都是一个子问题，因此你需要考虑如何将问题分解为子问题。

待补充。

K最近邻算法

使用K最近邻算法可以帮助我们在现实生活中完成下面的事情：

• 在外卖平台给你推荐你可能喜欢的餐食。
• 在电影网站给你推荐你可能喜欢的电影。
• 在购物平台给你推荐你可能喜欢的商品。
• 预测明天的销量。
• 创建垃圾邮件过滤器。
• 预测股票市场(中国股市，还是算了吧)。

该算法体现了，人以类聚物以群分。找出我们最近的一些朋友，通过提取一些通用特征，来预测出我们可能喜欢的一些东西。没错，推荐系统就是用它，它可能是你进入机器学习领域的领路人。

该算法主要会经历两个重要步骤：

• 通用特征提取，通过对两个事物的公共特征的计算，获取他们对应的矢量距离(每个特征可以当做一个维度的值)，通过这些计算将事物进行分类。挑选合适的特征很重要，所谓合适的特征，就是：与要推荐的事物紧密相关的特征；不偏不倚的特征（例如，如果只让用户给喜剧片打分，就无法判断他们是否喜欢动作片）。
• 通过分类后的数据集，进行回归，也就是预测结果。

注：在实际工作中，经常使用余弦相似度（cosinesimilarity），而非简单的计算矢量距离。假设有两位品味类似的用户，但其中一位打分时更保守。他们都很喜欢Manmohan Desai的电影Amar AkbarAnthony，但Paul给了5星，而Rowan只给4星。如果你使用距离公式，这两位用户可能不是邻居，虽然他们的品味非常接近。

布隆过滤器

当需要对大量数据进行去重时，如果使用散列表进行操作，将耗费大量的存储空间，布隆过滤器是引入了k(k>1)个相互独立的哈希函数，保证在给定的空间、误判率下，完成元素判重的过程。下图中是k=3时的布隆过滤器。

image

x,y,z经由哈希函数映射将各自在Bitmap中的3个位置置为1，当w出现时，仅当3个标志位都为1时，才表示w在集合中。图中所示的情况，布隆过滤器将判定w不在集合中。

布隆过滤器的优点在于占用的存储空间很少。使用散列表时，答案绝对可靠，而使用布隆过滤器时，答案却是很可能是正确的。可能出现错报的情况：

• 这个数据已存在，但实际上并没不存在。
• 不可能出现漏报的情况，即如果布隆过滤器说“这个数据不存在”，就肯定不存在。

参考

1. 《算法图解》作者：【美】Aditya Bhargava 译者：袁国忠
2. Bitmap和布隆过滤器(Bloom Filter)