TopK的常见解法

原文链接：https://bestzuo.cn/posts/12067206.html

TopK

在大规模数据处理中，经常会遇到TopK问题，也就是在海量数据中找到最大/小的k个数。这也是校招面试常问的算法题，TopK问题的应用场景很多，比如微博中找到搜索关键字中最热的10个词作为热搜、搜索引擎中找到一段时间中搜索次数最多的k个关键字，歌曲库中统计下载次数最多的k首歌曲等等。

思路优化

排序

最容易想到的肯定是排序算法，然后取其排序的最大/小的k个数就完事了。其时间复杂度是O(nlogn)，但是问题来了，如果前提是以亿为单位的数据，你还敢用排序算法吗？明明只需要k个数，为啥要对所有数都排序呢？并且对这种海量数据，计算机内存不一定能扛得住。

局部淘汰法

既然只需要k个数，那么我们可以再优化一下，先用一个容器装这个数组的前k个数，然后找到这个容器中最小的那个数，再依次遍历后面的数，如果后面的数比这个最小的数要大，那么两者交换。一直到剩余的所有数都比这个容器中的数要小，那么这个容器中的数就是最大的k个数。

这种算法的时间复杂度为O(n*m)，其中m为容器的长度。

具体地，其过程如下图所示：

image

那么这种方法的时间复杂度也太大，同样的思路，我们其实还可以利用最大/小堆来实现，这就引出了下一个实现方法。

堆

我们可以先用前k个元素生成一个小顶堆，这个小顶堆用于存储当前k个元素，例子同上，可以构造小顶堆如下：

image

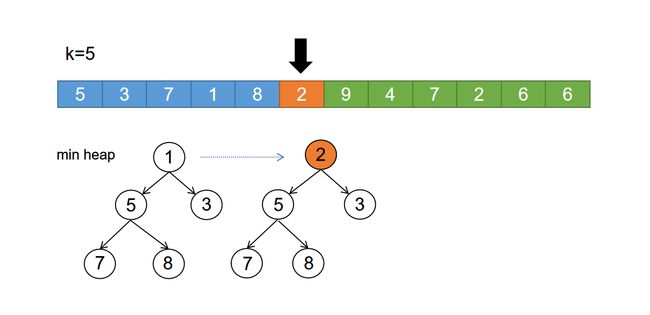
然后从第k+1个元素开始扫描，和堆顶元素比较（最小值），如果当前元素大于堆顶元素，则替换堆顶值，并调整堆，以保证堆内k个元素一直是当前最大的k个元素，如图所示：

image

直到，扫描完所有n-k个元素，最终堆中的k个元素，就是猥琐求的TopK：

image

这种堆解法的时间复杂度为O(N*logk)，并且堆解法也是求解TopK问题的经典解法，用代码实现如下：

public int findKthLargest(int[] nums, int k) {
    k = nums.length - k + 1;
    PriorityQueue pq = new PriorityQueue<>(Comparator.reverseOrder()); // 大顶堆
    for (int val : nums) {
        pq.add(val);
        if (pq.size() > k)  // 维护堆的大小为 K
            pq.poll();
    }
    return pq.peek();
}

那么还有没有更高效的解法呢？

快速排序

我们知道，快排的思想就是分治法，即分而治之，简而言之，就是把一个大问题分解为若干个子问题，然后把每个子问题都求解出来，最后整个大问题就解决了，其伪代码如下：

public void quick_sort(int[]arr, int low, inthigh){ 
     if(low== high) return; 
     int i = partition(arr, low, high); 
     quick_sort(arr, low, i-1); 
     quick_sort(arr, i+1, high); 
} 

那么其中的核心就在于partition(arr, low, high)上，这个partition是什么意思呢？顾名思义，就是通过这个方法把数组分为两部分。更具体地，就是以数组arr中的一个元素（一般默认是第一个元素t=arr[low]）作为划分依据，将数组arr[low,high]分为左右两个子数组：

• 左半部分，都比t小
• 右半部分，都比t大

如下图所示：

image

那么partition的返回结果就是t最终的位置i。

很容易知道，partition的时间复杂度为O(n)。

那么快排跟Topk问题有什么关系呢？回到问题本身，TopK就是希望求出数组arr[1,n]中最大的k个数，那么如果找到了第k大的数，做一次partition，不就一次性找到最大的k个数了么？结果也就是partition的右半区间的数。

那么问题最终就变成了找数组中第k大的数，回过头来看看第一次partition划分之后：

int i = partition(arr,1,n);

那么这时候有两种情况：

1. i > k，那么说明arr[i]左边的元素都大于k，于是只需要随后递归arr[1,i-1]里面第k大的元素即可；
2. i < k，那么说明第k大的元素在右边，于是只需要递归arr[i+1,n]里第k-i大的元素即可。

上面这段非常重要，可以多读几遍。

使用代码实现上述算法可以如下：

public int findKthElement(int[] nums, int k) {
    k = nums.length - k;
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int j = partition(nums, l, h);
        if (j == k) {
            break;
        } else if (j < k) {
            l = j + 1;
        } else {
            h = j - 1;
        }
    }
    return nums[k];
}

private int partition(int[] a, int l, int h) {
    int i = l, j = h + 1;
    while (true) {
        while (a[++i] < a[l] && i < h) ;
        while (a[--j] > a[l] && j > l) ;
        if (i >= j) {
            break;
        }
        swap(a, i, j);
    }
    swap(a, l, j);
    return j;
}

private void swap(int[] a, int i, int j) {
    int t = a[i];
    a[i] = a[j];
    a[j] = t;
}

TopK的其它问题

海量数据

海量数据前提下，肯定不可能放在单机上。

• 拆分，可以按照哈希取模或者其它方法拆分到多台机器上，并在每个机器上维护最小堆
• 整合，将每台机器上得到的最小堆合并成最终的最小堆

频率统计

找出一个数据流中最频繁出现的k个数，比如热门搜索词汇等。

• 使用HashMap进行频率统计，数据量不大时可用
• Count-Min Sketch方法，具体可以Google
• Trie树解决，可以参考这里

参考文章

1. TopK
2. 拜托，面试别再问我TopK了
3. 海量数据处理--topK问题
4. 海量数据处理问题（Top k问题）的实现