《生活中的算法 (Algorithms to live by)》第二章: 探索/利用
生活中总会碰到,需要决定是探索 (Explore)还是利用 (Exploit) 的场景。所谓探索即不固守现有信息,对未知事物进行探索,获得关于它们的新信息;而利用则是对自己已了解的事物进行充分利用,获得最大好处。
这样的场景很多,比如说我喜欢看书,所以喜欢收集好书。长期下来,就堆积了很多书看不完。同时,因为惦记这些看不完的书,导致对一些经典书没有进行精读。这算是探索过度吧,结果就是没把时间放在重要的东西上去,因此真正的收获反而少了。
另一方面,自进入自然语言处理(NLP)领域以来,起初还天天探索新知识技术。但之后因为需要集中精力做课题,就慢慢把精力放在很窄的范围了,每天就研究那些。但同时,很多值得研究的新技术不断出现,比如说生成对抗性网络 (GAN) 还有强化学习 (RL) 在NLP领域的成功应用。而自己对这些却不是很了解。在研究遇到困难,看到其他人在这些方向取得成果时,有时也会想当初要是研究那边课题就好了,有点后悔 (Regret).
如此可见,探索/利用问题在日常生活中是很常见的。而这一章便是讲如何利用探索/发现算法,来对此类问题作出决定。
基本问题
首先,这类问题最基本的原型是“多老虎机问题 (Multi-armed bandit problem)”。假设进入一个赌场,这里有很多台老虎机,设置了不同的胜率,但你并不知道。自然而然你为了最大化自己的收益,就需要到处探索找出胜率最高的机器,然后利用它来获得最大收益。
这个问题里处于哪个时间段 (interval)对你决定的影响非常大,比如说刚进入赌场时,自然是会优先进行探索。而当快要离开时,想在剩下的时间带走更多的钱,那就会优先利用,只玩胜率高的机器。
最初的策略:赢了继续,输了就换
第一个有名的策略是 Herbert Robbin 提出来的:赢了继续,输了就换。他考虑的是只有两台机器的情况,也就是说先随便找台机器玩,如果赢了就继续在这台上玩,输了换机器,赢了继续,输了就换...
虽然看上去很简单,但Robbin证明了这个策略要比单纯随机玩更好些。然而也因为过于简单,存在一个大问题。这个问题便是”输了就换“并不合理,想想如果你在一台机器上连续玩了十把都赢了,而只是突然输了一把,你会去换吗?作为一个理性人都不会的,而会继续玩,直到觉得这台机器的胜率其实小于某个预期。
第二个策略:Gittins 指数
在数学中总会出现一通百通的例子,对于一个问题的解决就是对一系列问题的解决。比如第二个策略的Gittins指数,实际上是Gittins在制药公司设计实验时提出来的。
制药公司做实验和多老虎机问题相似的地方在于,对于一个药,他们需要探索每个成分对病情的效果,使得在最少的试验次数下获得足够多的值得信任的数据,找出效果最好的成分。这里每个成分就相当于一台老虎机。
Gittins与其他研究者不同的是,他假设最大化的不是在一段时间内的收益,而是无限时间下单次收益会随着时间变长而打折扣的总收益。这个假设也很合理,比如说你就会更关心今晚吃什么,而不是明天吃什么。
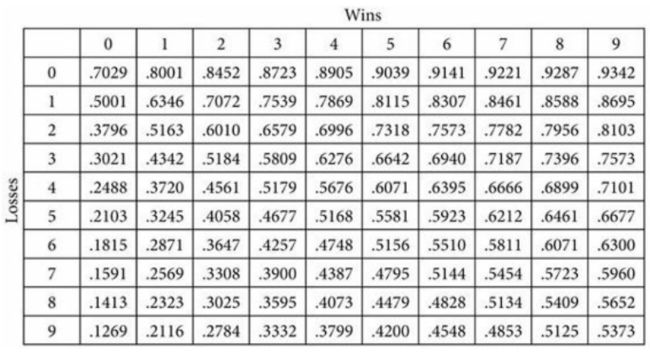
Gittins对此提出了一个策略,就是利用Gittins指数(也叫动态分配指数)来辅助决策。具体指数如下表,下表为下次收益为前一次90%的情况。
使用时,先给每台机器分配一个Gittins指数,然后挑出指数最大的机器玩,玩的时候根据表格更新指数,然后继续挑最大的,更新...
Gittins指数的一个显著特点是,给没有探索的机器也分配了高于期望值0.5的分数,也就是说鼓励探索。同时,Gittins指数的表格让解决方法非常简单直观。
但Gittins指数方法也有很多缺点,首先是它的假设,第二没有考虑换机器时产生的成本,最后也是最重要的,在日常生活中很难使用,很难一下子就计算出一张表格,即使带上表格也会因为条件改变表格也得变。
乐观的上置信界限算法
如果因为Gittins指数太复杂,或者你面对的问题并不满足其假设,那么你就可以试着把注意力放在后悔(Regret)上面,最小化你的后悔,而不是最大化收益。
人最容易后悔的情况是什么,就是之前自己没有鼓起勇气去选择做某事,之后发现别人做这件事成功了。比如说,不敢搭讪一位女生,结果发现别人搭讪成功了,还交往起来了,心中肯定就会特别后悔。这里之所以出现这种情况,是因为你在担心最坏情况(被拒绝,男友出现被打),也就是下置信界限。而由Robbins还有Lai提出的上置信界限算法则认为我们考虑最好的情况会更好。
首先什么是置信界限(Confidence Bound),即变动的可能性。比如说,有一台从没探索过的老虎机,那么它就具有无限的可能性,可能胜率为0,也可能为100%。此时,置信界限就非常大,而随着探索次数增加,对老虎机的胜率慢慢心里有了底,此时置信界限就会慢慢收敛变小。再如小说里什么“莫欺少年穷”,就表示年轻人置信界限大,未来可能分分钟打你脸。
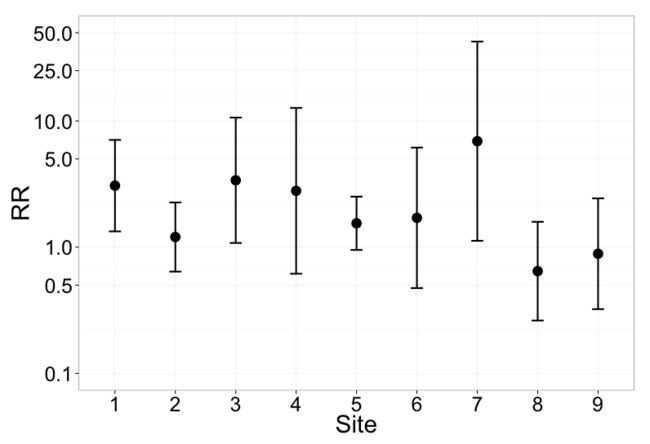
在现实生活中表示置信界限时,可以用如折线图中的误差条 (Error bar)来表示。
上置信界限算法策略,就是在所有选择中挑选上置信界限最大的一个选项。如果转化成现实策略,那就是始终相信一件事可能的最好结果,也就是面对不确定时,始终乐观往最好想,然后挑选最好中的最好。
和Gittins指数方法相似,上置信界限算法也给没有探索的选项比期望值高的分数,这样会鼓励对未知选项进行更多的探索。而与Gittins指数不同的是,上置信界限更加容易计算一些。
至于从这里学到了什么,那就是,下次男生看到美女时就想着,最好的情况她可能成为你的女朋友哦,然后勇敢搭讪。
更多的例子:A/B测试,临床试验
类似多老虎机问题的问题,现实中有很多,其中有些非常很重要,有时是一个国家的命运或一个人的生命。
比如说奥巴马选举时,为了进行有效募捐,他的“新媒体分析”团利用A/B测试(类似赢了继续策略)对各个选项对进行了对比和探索,之后选择最好的组合。结果成功募捐到了5700万的额外捐款。
还有医学临床实验,对比两个疗法的效果,也和多老虎机问题类似。如果能够利用好的算法来处理此类问题,那么就可以避免无谓的死亡。这里举了ECMO(叶克膜)疗法的例子,因为不合理的实验结果导致了过多孩子的牺牲。
多变的世界
现实生活往往很多问题要比多老虎机问题更加复杂,因为世界是多变的。就好像这些老虎机随着时间,胜率也在变化,之前探索的结论现在可能以及没用了。楼下理发店的Kevin老师,进修完之后,说不定已经成了一流理发师。
多变的世界给了我们一个启示,要多进行探索,即使是之前探索过认为是不好的选项,说不定已经变成好选项。
但是,对于这个多变问题,现在还没有进行有效解决的算法,而且未来可能也不会有了。
那么既然这样,之前说的算法就都没用了咯,也不是。现实中很多东西很大程度上还是符合上面的那些假设,不然也不会得到实际应用。
其实上面这些算法最重要的并不是告诉我们怎么解决问题,而是提供了一个看待人生的新视角:探索与利用的取舍,时间段的重要性,未知的重要性,最小化后悔...
通过这个新的视角我们才能更合理地做出可能影响一生的决定。
怎么过一个没有遗憾的人生
回到主题,怎么过一个没有遗憾的人生?
通过阅读本章我认为:在年轻时,以一种乐观积极的态度来对未知选项进行探索,通过长时间的探索发现好的选项,当到了一定年龄则开始主要注重于利用已知的好选项。当然,因为多变世界的原因,还是要对已有的这些选项进行一定的重新探索。