KMP算法及优化

转载请注明出处: KMP算法及优化

今天看到同学在复习数据结构书上的KMP算法，忽然发觉自己又把KMP算法忘掉了，以前就已经忘过一次，看样子还是没有真正的掌握它，这回学聪明点，再次搞明白后记录下来。

---

一般字符串匹配过程

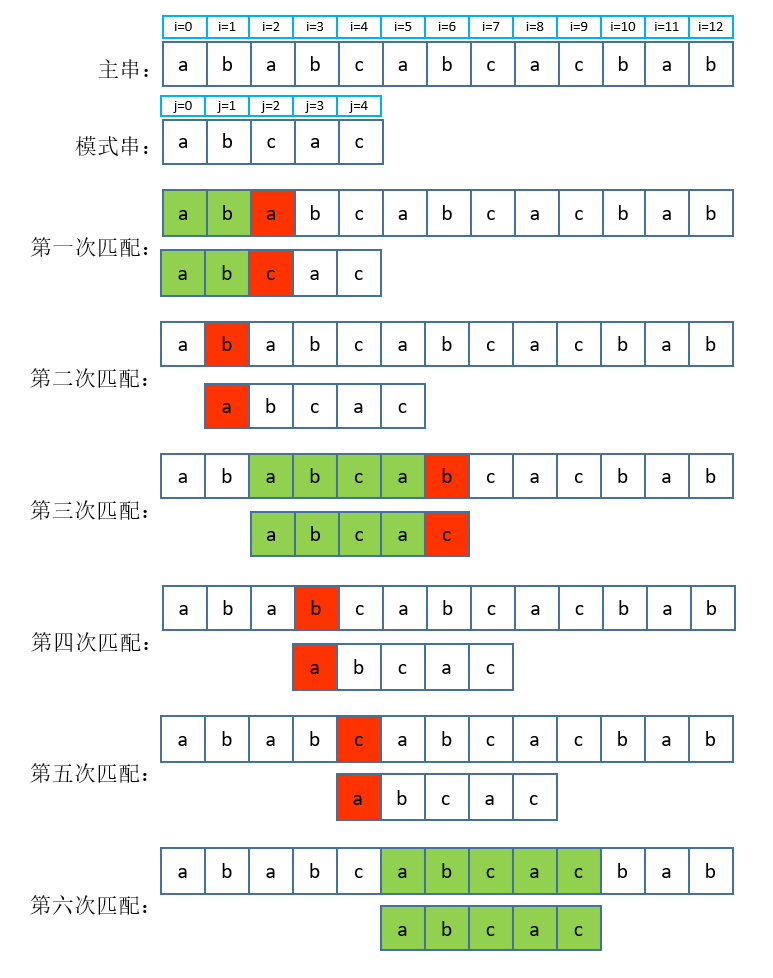
KMP算法是字符串匹配算法的一种改进版，一般的字符串匹配算法是：从主串(目标字符串)和模式串(待匹配字符串)的第一个字符开始比较，如果相等则继续匹配下一个字符， 如果不相等则从主串的下一个字符开始匹配，直到模式串被匹配完，则匹配成功，或主串被匹配完且模式串未匹配完，则匹配失败。匹配过程入下图：

一般匹配方法.PNG

这种实现方式是最简单的， 但也是低效的，因为第三次匹配结束后的第四次和第五次是没有必要的。

分析

第三次匹配在j = 0(a)和i = 2(a)处开始，在j = 4(c)和i = 6(b)处失败，这意味着模式串和主串中：j = 0(a)和i = 2(a)、j = 1(b)和i = 3(b)、j = 2(c)和i = 4(c)、j = 3(a)和i = 5(a)这四个字符相互匹配。

分析模式串的前3个字符：模式串的第一个字符j = 0是a，j = 1(b)、j = 2(c)这两个字符和j = 0(a)不同，因此以这两个字符开头的匹配必定失败，在第三次匹配中，主串中i = 3(b)、i = 4(c)和模式串j = 1(b)、j = 2(c)相互匹配，因此匹配失败后，可以直接跳过主串中i = 3(b)、i = 4(c)这两个字符的匹配。

继续分析模式串的j = 3(a)和j = 4(c)这两个字符，如果模式串匹配到j = 4(c)这个字符才失败的话，因为j = 4(c)的前一个字符j = 3(a)和第一个字符j = 0(a)是相同的，结合上一个分析得知：

1)：下一次匹配中主串已经跳过了和j = 3(a)前两个相互匹配的字符i = 3(b)、i = 4(c)，将从i = 5(a)开始匹配。
2)：j = 3(a)和i = 5(a)相互匹配。

因此下一次匹配认为j = 3(a)和i = 5(a)已经匹配过了，匹配从j = 4(b)和i = 6(b)开始，这样的话也跳过了j = 3(a)这个字符的匹配。

同理可得第二次匹配也是没必要的。

KMP算法

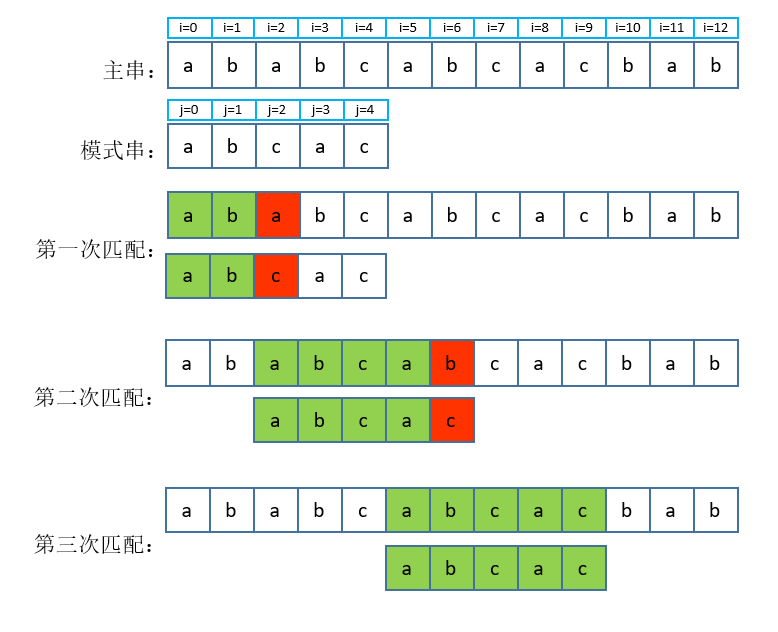
KMP算法匹配过程

利用KMP算法匹配的过程如下图：

KMP算法匹配过程.PNG

KMP算法的改进之处在于：能够知道在匹配失败后，有多少字符是不需要进行匹配可以直接跳过的，匹配失败后，下一次匹配从什么地方开始能够有效的减少不必要的匹配过程。

next[n]求解方法

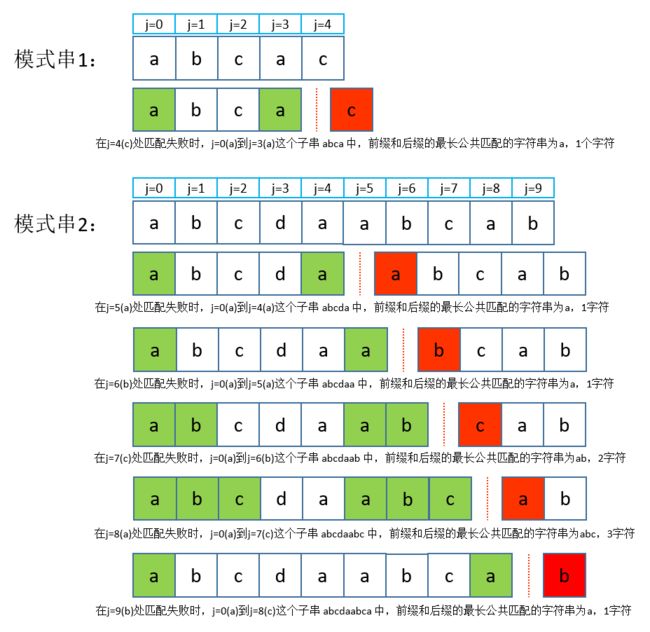
由上面的分析可以发现，KMP算法的核心在于对模式串本身的分析，其分析结果能提供在j = n位置匹配失败时，从j = 0到j = n - 1这个子串中前缀和后缀的最长公共匹配的字符数，这样说可能比较难以理解，看下图：

最长公共匹配字符数.PNG

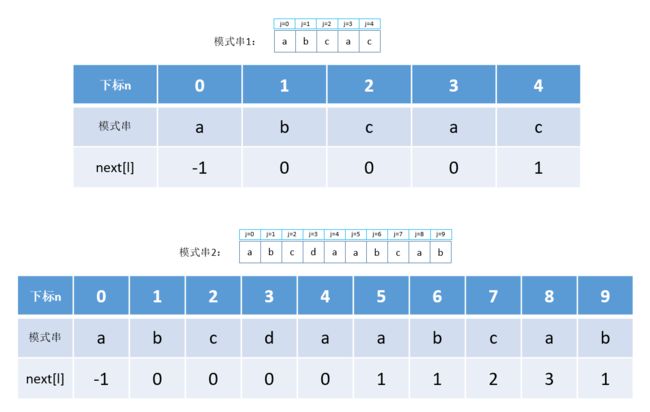
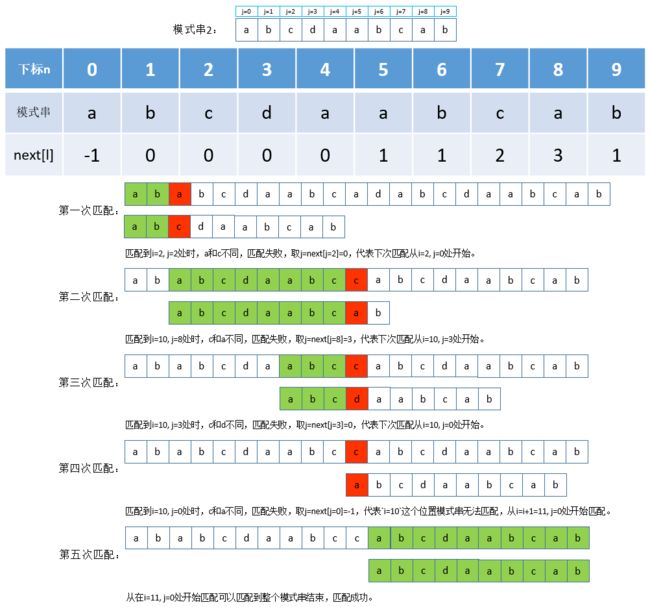
在得到子串前缀和后缀的最长公共匹配字符数l后，以后在i = x,j = n处匹配失败时，可以直接从i = x,j = l处继续匹配(证明过程参考:严蔚敏的《数据结构》4.3章)，这样问题就很明显了，我们要求出n和l对应的值，其中n是模式串字符数组的下标，l的有序集合通常称之为next数组，前面两个模式串的next数组和下标n的对应如下：

next[l].PNG

模式串2完整匹配过程

有了这个next数组，那么在匹配的过程中我们就能在j = n处匹配失败后，根据next[n]的值进行偏移，其中next[0]固定为-1，代表在当前i这个位置整个模式串和主串都无法匹配成功，要从下一个位置i = i + 1及j = 0处开始匹配，模式串2的匹配过程如下：

模式串2匹配过程.PNG

现在知道了next数组的作用，也知道在有next数组时的匹配过程，那么剩下的问题就是如何通过代码求出next数组及匹配过程了。

求next数组的过程可以认为是将模式串拆分成n个子串，分别对每个子串求前缀和后缀的最长公共匹配字符数l，这一点可以通过上图(最长公共匹配字符数)看出来(没有画出l=0时的图解)看出来。

代码实现

求next数组的代码如下：

void get_next(string pattern, int next[]) {
    int i = 0; // i用来记录当前计算的next数组元素的下标， 同时也作为模式串本身被匹配到的位置的下标
    int j = 0; // j == -1 代表从在i的位置模式串无法匹配成功，从下一个位置开始匹配
    next[0] = -1; // next[0]固定为-1
    int p_len = pattern.length();
    while (++i < p_len) {
        if (pattern[i] == pattern[j]) {
            // j是用来记录当前模式串匹配到的位置的下标， 这就意味着当j = l时，
            // 则在pattern[j]这个字符前面已经有l - 1个成功匹配,
            // 即子串前缀和后缀的最长公共匹配字符数有l - 1个。
            next[i] = j++;
        } else {
            next[i] = j;
            j = 0;
            if (pattern[i] == pattern[j]) {
                j++;
            }
        }
    }
}

根据next数组求模式串在主串中的位置代码如下：

int search(string source, string pattern, int next[]) {
    int i = 0;
    int j = 0;
    int p_len = pattern.length();
    int s_len = source.length();
    while (j < p_len && i < s_len) {
        if (j == -1 || source[i] == pattern[j]) {
            i++;
            j++;
        }
        else {
            j = next[j];            
        }
    }
    if (j < pattern.length())
        return -1;
    else
        return i - pattern.length();
}

测试代码如下：

int main() {
    string source = "ABCDABCEAAAABASABCDABCADABCDABCEAABCDABCEAAABASABCDABCAABLAKABCDABABCDABCEAAADSFDABCADABCDABCEAAABCDABCEAAABASABCDABCADABCDABCEAAABLAKABLAKK";
    // string pattern = "abcaaabcab";
    string pattern = "ABCDABCEAAABASABCDABCADABCDABCEAAABLAK";
    int next[pattern.length()] = { NULL };
    get_next(pattern, next);
    cout << "next数组: \t";
    for (int i = 0; i < pattern.length(); i++)
        cout << next[i] << " ";
    cout << endl;
    int pos = search(source, pattern, next);
    if (-1 != pos) {
        cout << "匹配成功，模式串在主串中首次出现的位置是: 第" << pos + 1 << "位";
        getchar();
        return 0;
    } else {
        cout << "匹配失败";
    }
    getchar();
    return 0;
}

执行结果：

next数组: -1 0 0 0 0 1 2 3 0 1 1 1 2 1 0 1 2 3 4 5 6 7 1 0 1 2 3 4 5 6 7 8 9 10 11 12 0 1 
匹配成功，模式串在主串中首次出现的位置是: 第97位

KMP算法优化

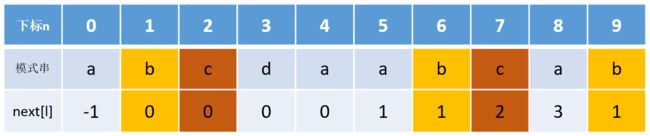
再回过头去看模式串2的next数组的图：

模式串2的next[n].PNG

如果模式串和主串的匹配在j = 6(b)处失败的话，根据j = next[6] = 1得知下一次匹配从j = 1处开始，j = 1处的字符和j = 6处的字符同为c，因此这次匹配必定会失败。
同样的，模式串和主串的匹配在j = 7(c)处或在j = 9(b)处失败的话，根据next数组偏移后下一次匹配也必定会失败。

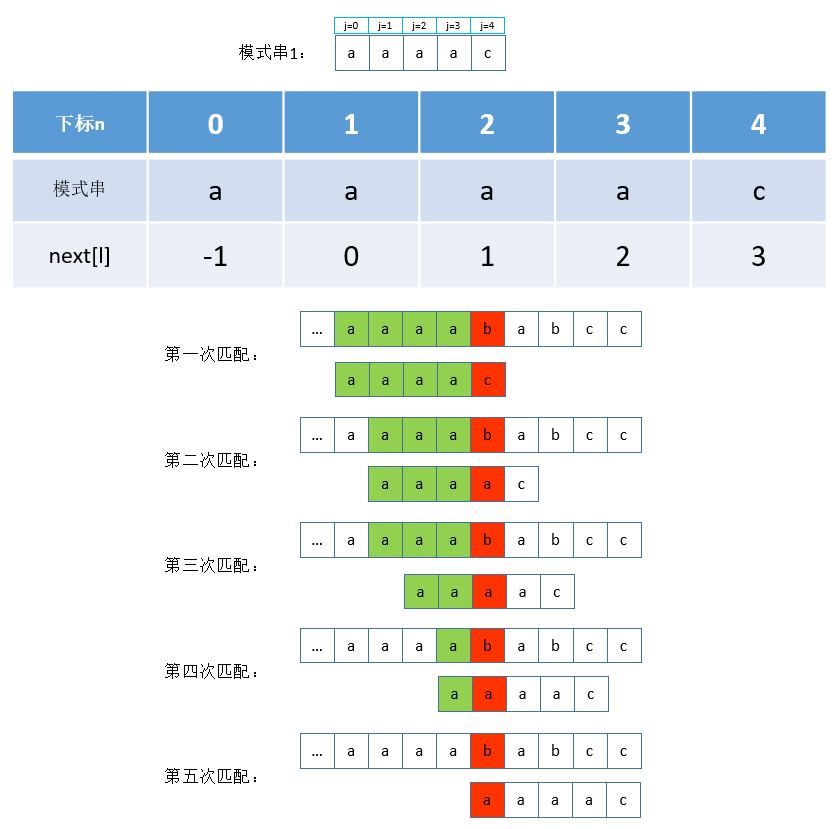
考虑如果模式串是: aaaac，根据一般的KMP算法求出的next数组及匹配过程如下：

KMP算法无效匹配过程.PNG

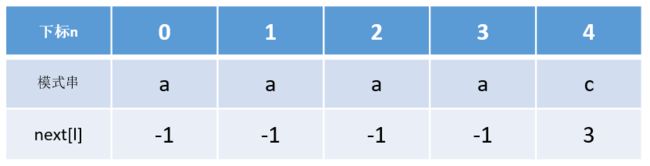
显而易见，在第二次匹配失败后，第三、四、五次匹配都是没有意义的，j = next[3]、j = next[2]、j = next[1]、j = next[0]这四处的字符都是a，在j = 3(a)处匹配失败时，根据模式串本身就应该可以得出结论：可以跳过j = 2(a)、j = 1(a)、j = 0(a)的匹配，直接从i = i + 1 、j = 0处开始匹配，所以优化过后的next数组应该是：

优化过后的next数组.PNG

代码实现

优化后的求next数组的代码如下：

void get_next(string pattern, int next[]) {
    int i = 0; // i用来记录当前计算的next数组元素的下标， 同时也作为模式串本身被匹配到的位置的下标
    int j = 0; // j == -1 代表从在i的位置模式串无法匹配成功，从下一个位置开始匹配
    next[0] = -1; // next[0]固定为-1
    int p_len = pattern.length();
    while (++i < p_len) {
        if (pattern[i] == pattern[j]) {
            // j是用来记录当前模式串匹配到的位置的下标， 这就意味着当j = l时，
            // 则在pattern[j]这个字符前面已经有l - 1个成功匹配,
            // 即子串前缀和后缀的最长公共匹配字符数有l - 1个。
            next[i] = j++;
            
            // 当根据next[i]偏移后的字符与偏移前的字符向同时
            // 那么这次的偏移是没有意义的，因为匹配必定会失败
            // 所以可以一直往前偏移，直到
            // 1): 偏移前的字符和偏移后的字符不相同。
            // 2): next[i] == -1
            while (next[i] != -1 && pattern[i] == pattern[next[i]]) {
                next[i] = next[next[i]];
            }
        } else {
            next[i] = j;
            j = 0;
            if (pattern[i] == pattern[j]) {
                j++;
            }
        }
    }
}

结尾

希望本文能对你有帮助， 如果有什么问题， 欢迎探讨。

参考文献

严蔚敏的《数据结构》4.3章
kmp算法--百度百科