现在对于一款拼音输入法来说,智能整句功能已可算是标配,所以我早就下定决心,必须给岁寒输入法也配一个。经过一段时间的潜心研究,这个目标终于在近日达成,最新版本的iOS岁寒输入法已经整合进了我开发出来的智能整句引擎,效果相当理想。
虽然网上介绍拼音整句的文章也是不少,但没有哪一篇文章能指导人从头到尾地完成一个整句引擎的开发。今天借这篇文章,我除了与大家分享我的开发心得,也希望每一个看完我这篇文章的朋友都可以实现一个自己的整句引擎,而且是可实用的整句引擎。为了达到这一目标,我会将本文写成整句引擎的开发指南,也是对iOS岁寒输入法现正使用的整句引擎作技术揭秘。
而以我个人之力,是难以完全独立地完成一个整句引擎的开发任务的,我也是站在巨人的肩膀上。在这里必须感谢郭家宝先生无私地开源了他所开发的拼音整句模型和相关数据,可从此处获得(郭家宝:基於統計語言模型的拼音輸入法。特此声明,岁寒整句引擎中使用了郭家宝先生开发的模型中的思想、数据和部分代码。
需要指出的是,郭先生所开发的整句模型是一个供学术研究之用的程序,并不能满足实际使用的需求,因为在程序启动时有比较漫长的数据加载过程,而且加载的数据量也很巨大,光是2元数据的文本文件大小就有70m之多,这对于iOS输入法40m左右的内存限制而言,是不可接受的。而且该模型也不支持拼音的省略输入,因此需要重写代码以满足实际应用的需要。此处绝非贬低郭先生所开发的整句模型,而是其程序开发的目标是为学术研究,所以理所当然不会考虑这些限制。从郭先生的程序中我受益匪浅,再次表示感谢。
统计语言模型
我所开发的整句引擎的理论基础是统计语言模型,这是目前最成功的整句模型。搜狗、百度、谷歌所开发的输入法也是使用的该模型,只不过人家工作做得更加精细,数据更加完备,所以效果更好,但大体的架构是类似的。
《数学之美》中是如此介绍统计语言模型的:
统计语言模型是为自然语言这种上下文相关的特性建立的数学模型,它是今天所有自然语言处理的基础,并且广泛应用于机器翻译、语音识别、印刷体或手写体识别、拼写纠错、汉字输入和文献查询。
可见统计语言模型并不止用于智能整句,用途十分广泛,它的其它应用在此是题外话,但个中原理是一样的。
假使S是一个有意义的句子,由一串特定顺序排列的词W1,W2,...,Wn组成,这里n是句子的长度。
要计算S在文本中的概率,即是计算P(S),有:
P(S)=P(W1,W2,...,Wn)
将P(W1,W2,...Wn)展开:
P(W1,W2,...,Wn) = P(W1)P(W2|W1)...P(Wn|W1,W2,...,Wn-1)
其中P(W1)表示第一个词W1出现的概率;P(W2|W1)表示已知第一个词的前提下,第二个词出现的概率;以此类推。词Wn的出现概率则取决于它前面的所有词;
但P(Wn|W1,W2,...,Wn-1)太过复杂,我们用马尔可夫假使对其作简化:假设任意一个词Wi出现的概率只同它前面的词Wi-1有关;
则有:
P(S)=P(W1)P(W2|W1)P(W3|W2)...P(Wi|Wi-1)...P(Wn|Wn-1)
这就是所谓的二元模型,也是我们整句引擎中所使用的模型;
如果我们假使Wi出现的概率只同它前面的2个词有关,则会得到三元模型;虽然使用三元模型效果会更好,但三元模型需要的数据量要大许多,四元以上就更不必说了。
对上面的公式两边取自然对数,则:
log[P(S)]
=log[P(W1)P(W2|W1)P(W3|W2)...P(Wi|Wi-1)...P(Wn|Wn-1)]
=log[P(W1)]+log[P(W2|W1)]+log[P(W3|W2)]+...+log[P(Wi|Wi-1)]+...+log[P(Wn|Wn-1)]
这一操作是必要的。由此,乘法被转换成加法,这样一来,后面我们对log[P(Wi|Wi-1)]取反(log[P(Wi|Wi-1)]<0),通过求解图的最短路径即可得到最大的P(S);
数据准备
巧妇难为无米之炊,没有数据,统计语音模型是玩不转的。
假使我们的统计样本的大小为C,词Wi的出现频度为C(Wi),词Wi-1和Wi连续出现的频度为C(Wi-1,Wi),则有:
P(Wi) = C(Wi)/C
P(Wi|Wi-1) = C(Wi-1,Wi)/C(Wi-1)
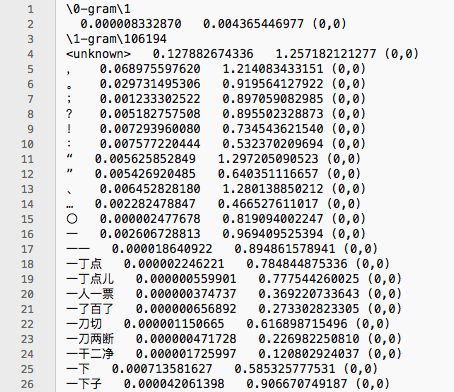
我们当然没有必要自己去训练数据,郭先生所使用的数据来自open-gram,也是遵循开源协议的,我们打开这个文件来看一看:
我阅读郭的代码后知道,倒数第三列数据即为前面字符串出现的统计概率,倒数两列的数据功用则不清楚,因为程序中并没有使用到。
将这些数据读入内存肯定是不可取的,比较方便的办法是将其放入sqlite数据库文件中以供查询。但我仍嫌这一做法生成的文件太大,也不是最适合在数据库中进行索引的格式。对于数据库而言,数字自然是最方便索引的类型,因此,我决定将字符串哈希化,即只保留字符串的哈希码和相应的概率,而不保留其内容。
经过实验,在使用32位长度对这130万的数据进行哈希化时,出现了大约8350次碰撞,频率还是有点高的。而使用64位时,则无一碰撞,因此选定64位长度保存long型字符串的哈希码,外加64位的double型保存统计概率。
我所使用的求long型哈希码的代码如下:
static long[] byteTable = createLookupTable();
static long HSTART = 1349303770470715811L;
static long HMULT = 7664345821815920749L;
private static long[] createLookupTable()
{
long[] byteTable = new long[256];
long h = 0x544B2FBACAAF1684L;
for (int i = 0; i < 256; i++)
{
for (int j = 0; j < 31; j++)
{
h = (h >> 7) ^ h;
h = (h << 11) ^ h;
h = (h >> 10) ^ h;
}
byteTable[i] = h;
}
return byteTable;
}
public static long hashCode(String cs)
{
long h = HSTART;
long hmult = HMULT;
long[] ht = byteTable;
int len = cs.Length;
for (int i = 0; i < len; i++)
{
char ch = cs[i];
h = (h * hmult) ^ ht[ch & 0xff];
h = (h * hmult) ^ ht[(ch >> 8) & 0xff];
}
return h;
}
表的格式如下:
CREATE TABLE "hashtable" ("hashcode" integer ,"probability" float );
最后生成的数据库文件大小为34.2m,这样的大小打包到安装包中还是可以接受的。为了提高表的查询速度,我们可以将hashcode键声明为unique,但这样会使数据文件体积增大一倍。另一个方案是在使用数据文件之前,建立一个unique的索引即可收到相同的效果。建立完索引的数据库文件会增加到57.3m,但这增加的部分并不会影响安装包的大小。
CREATE UNIQUE INDEX "hashtable_hashcode" on "hashtable"("hashcode");
使用哈希化的优化方式相对来说是比较激进的,也就是说在使用过程中有可能会出现哈希碰撞的可能性,但鉴于130万词无一碰撞,相信这概率很小很小,应该不会影响实际使用,甚至采用32位哈希码也不是不可以考虑的。
此外,我们还要准备一个词库,这个词库是用查询词组信息的,词库中至少应该包含如下几项信息:词组的字符内容,对应的拼音及使用词频。这样一个词库并不需要很大,像岁寒输入法所用的默认词库,大小为15万词左右,能够包含我们日常所使用的大多数常用词即可。这个词库中也应该建立响应的索引以提高查询速度。
图的定义
对于整个整句引擎而言,最重要的数据结构莫过于图了。图分无向图和有向图,无权图和加权图,有环图和无环图。在这里,我们会用到有向无权无环图和有向加权无环图。
图,作为一个基础性的数据结构,在此就不多作介绍了,感兴趣的朋友可以随便找一本数据结构方面的书籍作参考,一般都有涉及。这里我推荐《算法》一书。
以下是我所使用的图的定义:
public class Graph
{
/***
* 顶点的定义
*/
public class Vertex
{
public List from;//入边的集合
public List to;//出边的集合
public object data;
public int id;
public Vertex(int id)
{
this.from = new List();
this.to = new List();
this.data = null;
this.id = id;
}
public override string ToString()
{
return data.ToString();
}
}
/***
* 边的定义
*/
public class Edge
{
public Vertex from;//指出该边的顶点
public Vertex to;//边所指向的顶点
public object data;
public Edge(Vertex from, Vertex to)
{
this.from = from;
this.to = to;
this.data = null;
}
}
protected Vertex[] vertex;//图中所有的顶点
protected LinkedList edges = new LinkedList();//图中所有的边
protected int vertex_count = 0;//顶点的数量
protected int edge_count = 0;//边的数量
public int VertexCount
{
get { return vertex_count; }
}
public int EdgeCount
{
get { return edge_count; }
}
protected void InitializeVertex()
{
vertex = new Vertex[vertex_count];
for (int i = 0; i < vertex_count; i++)
{
vertex[i] = new Vertex(i);
}
}
/**
* 添加一条边的方法
*
*/
protected virtual Edge AddEdge(Vertex from, Vertex to)
{
Edge e = new Edge(from, to);
from.to.Add(e);
to.from.Add(e);
edge_count++;
edges.AddLast(e);
return e;
}
/**
* 返回给定顶点的所有出边
*/
public List adjEdge(int v)
{
return Vertexes[v].to;
}
/**
* 返回给定顶点的所有出边所指向的顶点的索引;
*/
public List adj(int v)
{
var result = new List();
var edges = vertex[v].to;
foreach (var i in edges)
{
result.Add(getIndex(i.to));
}
return result;
}
public int getIndex(Vertex i)
{
return i.id;
}
public Vertex[] Vertexes
{
get { return vertex; }
}
public LinkedList Edges
{
get { return edges; }
}
}
需要说明一下,这篇文章中所使用编程语言为C#,平台为xamarin studio。
建立拼音图
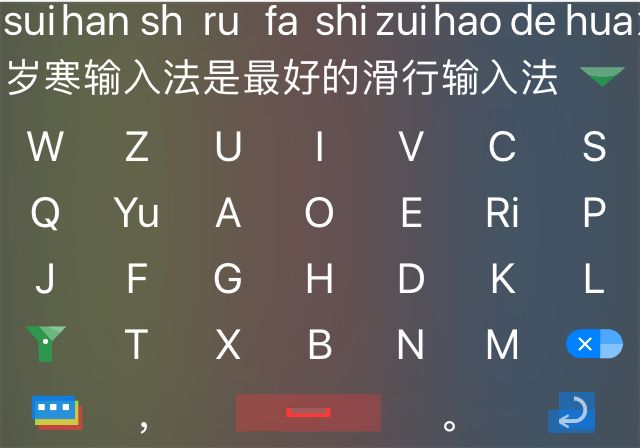
假使我们要整句的目标是这么一句话:“我们一定要打败所有的敌人”,其拼音的一般表示为“wo'men'yi'ding'yao'da'bai'suo'you'de'di'ren”,其在岁寒输入法中声母和韵母是分开表示的,所对应的声母是“wmydydbsyddr”,韵母是“oIiPFaDX4eiI”。这个表示看起来好像不太对劲,韵母怎么是这样子的。其实很简单,这是因为我用一个字母或数字来表示一个声母或韵母。这样表示的好处除了减少存储的空间,同时也会提高数据库索引的速度,而将声母和韵母分开更利于实现省略输入。在代码中我处理的拼音形式如上,但在下面的图解中我会使用一般的表示。
如果你不是如此表示拼音的,也没有关系,形式上的差异并不会影响本质。如果你想知道如何将字母序列转化成拼音序列,可以参考郭先生的代码。这一部分并不复杂,只要实现不是太糟糕,都不至于引发性能上的问题。
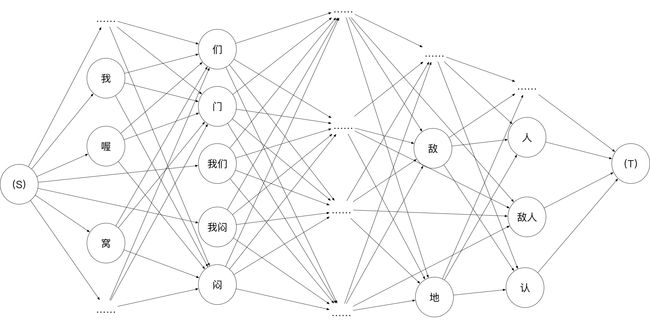
我们需要根据给定的拼音序列构造一个以拼音为顶点,以词组为边的有向无权无环图,其形状如下。
这个图的构造十分简单,就是将拼音序列中所有可能的单字、二字词、三字词一直到N字词都找出来。但在实际中太长的词组价值不大,因此我们取到4字词或5字词就差不多了,至少大多数的成语就不会被忽略了。
以下是构造拼音图的LexiconGraph类,注意LexiconGraph继承自Graph:
public class LexiconGraph : Graph
{
public LexiconGraph()
{
}
public LexiconGraph(String sheng, String yun)
{
/*
* 顶点的数量比拼音的数量多一个,对应图中的(T),
* 如果没有这个顶点,为单字添加边时就会形成自环
*/
vertex_count = sheng.Length + 1;
InitializeVertex();
for (int i = 1; i < 5; i++)
{
for (int j = 0; i + j <= sheng.Length; j++)
{
var list = LexiconLib.Instance.getPhrases(sheng.Substring(j, i), yun.Substring(j, i));
foreach (var v in list)
{
Edge e = AddEdge(vertex[j], vertex[i + j]);
var data = new EdgeData();
data.phrase = v;
data.id = this.edge_count;
e.data = data;
}
}
}
}
/**
* 用于携带词组信息的类
*/
public class EdgeData
{
public int id;
public string phrase;
public EdgeData()
{
}
}
}
其中的LexiconLib是用于与数据库对接的查询类,其定义如下:
public class LexiconLib {
Dictionary> zis = new Dictionary>();
Dictionary> cis = new Dictionary>();
static LexiconLib instance;
public static LexiconLib Instance {
get {
if (instance == null) {
instance = new LexiconLib();
}
return instance;
}
}
public LexiconLib() {
}
public void clearCis() {
cis.Clear();
}
public List getPhrases(String sheng, String yun) {
String key = sheng + yun;
if (sheng.Length == 1) {
if (!zis.ContainsKey(key)) {
StringBuilder stringBuilder = new StringBuilder("select distinct * from zi where ");
addCondition(sheng, yun, stringBuilder);
stringBuilder.Append("order by fre desc limit 15;");
var list = (from e in SuiHanConnetionFactory.MainDataBase.Query(stringBuilder.ToString(), new String[] { sheng, yun }) select e.Str).ToList();
zis.Add(key, list);
return list;
}
return zis[key];
} else {
if (!cis.ContainsKey(key)) {
StringBuilder stringBuilder = new StringBuilder("select distinct * from ci where ");
addCondition(sheng, yun, stringBuilder);
stringBuilder.Append("order by fre desc limit 10;");
var list = (from e in SuiHanConnetionFactory.MainDataBase.Query(stringBuilder.ToString(), new String[] { sheng, yun }) select e.Str).ToList();
cis.Add(key, list);
return list;
}
return cis[key];
}
}
static void addCondition(string sheng, string yun, StringBuilder stringBuilder) {
stringBuilder.Append(sheng.Contains("?") ? "sheng glob ? " : "sheng = ?");
stringBuilder.Append(" and ");
stringBuilder.Append(yun.Contains("?") ? "yun glob ? " : "yun = ?");
}
}
其中,SuiHanConnetionFactory.MainDataBase就是岁寒输入法的词库对象。
我将字和词分作两表存储,所以必须分开查询。
而order by fre desc limit 10;语句则是对查询结果进行排序,并限制其数量,词频太靠后的词组价值不大,我们没有必要取出所有的词组,在省略输入时尤其如此。而限制取词的数量,可以极大地提高引擎的整句速度。
此外,我还对查询结果进行了缓存,这是必要的。因为在实际使用过程中,用户的输入是渐进的。比如说,用户先输入了“wo”,再输入了“men”,那么上一次对“wo”的查询结果,在这一次构造拼音图的过程中也是有用的。其重要性,我们最后通过实验可以看到。
addCondition方法中对SQL语句作了优化,同时也是实现省略输入的关键,除了省略韵母,还可以省略声母。
建立词组图
有了拼音图,下面我们要基于拼音图构造词组图,其形状大致如下:
图中我并没有将边的权重标出来,事实上,这是一个以词组为顶点,以转移概率为边的有向加权无环图。
从拼音图到词组图的转换类如下:
public class SLMGraph : Graph
{
public SLMGraph(LexiconGraph lexicon_graph)
{
/**
* 顶点的数量比词组的总数多两个,分别用作起始顶点和终止顶点
*/
this.vertex_count = lexicon_graph.EdgeCount + 2;
InitializeVertex();
for (int i = 0; i < vertex_count; i++)
{
vertex[i].data = new VertexData();
}
//设置所有的顶点的词组信息
foreach (Edge e in lexicon_graph.Edges)
{
int id = (e.data as LexiconGraph.EdgeData).id;
(vertex[id].data as VertexData).phrase = (e.data as LexiconGraph.EdgeData).phrase;
}
(vertex[0].data as VertexData).phrase = "(S)";
(vertex[vertex_count - 1].data as VertexData).phrase = "(T)";
//创建从起始顶点指出的边
foreach (Edge e in lexicon_graph.Vertexes[0].to)
{
int id = (e.data as LexiconGraph.EdgeData).id;
AddEdge(0, id, GetUnigram((e.data as LexiconGraph.EdgeData).phrase));
}
//创建指向终止顶点的边
foreach (Edge e in lexicon_graph.Vertexes[lexicon_graph.VertexCount - 1].from)
{
int id = (e.data as LexiconGraph.EdgeData).id;
AddEdge(id, vertex_count - 1, new Weight().setValue(1));
}
//创建图中的其它边
for (int i = 0; i < lexicon_graph.VertexCount; i++)
{
foreach (Edge eprev in lexicon_graph.Vertexes[i].from)
{
int prev_id = (eprev.data as LexiconGraph.EdgeData).id;
string prev_phrase = (eprev.data as LexiconGraph.EdgeData).phrase;
foreach (Edge esucc in lexicon_graph.Vertexes[i].to)
{
int succ_id = (esucc.data as LexiconGraph.EdgeData).id;
string succ_phrase = (esucc.data as LexiconGraph.EdgeData).phrase;
AddEdge(prev_id, succ_id, GetBigram(prev_phrase, succ_phrase));
}
}
}
//处理所有的未知的转移概率(权重)
ProbabilityLib.Instance.dealUnknownWeights();
}
/**
* 获得二元转移概率
*/
Weight GetBigram(string prev_phrase, string succ_phrase)
{
return ProbabilityLib.Instance.GetBigram(prev_phrase, succ_phrase);
}
/**
* 获得一元转移概率
*/
Weight GetUnigram(string phrase)
{
return ProbabilityLib.Instance.GetUnigram(phrase);
}
protected Edge AddEdge(int from, int to, Weight weight)
{
Edge e = base.AddEdge(vertex[from], vertex[to]);
e.data = new EdgeData();
(e.data as EdgeData).weight = weight;
return e;
}
/**
*
* 用于携带转移概率的边数据类
*/
public class EdgeData
{
public Weight weight = null;
}
/**
* 用于携带词组的顶点数据类
*/
private class VertexData
{
public string phrase = null;
public override string ToString()
{
return phrase;
}
}
}
查询转移概率
创建词组图的过程中,会创建成千上万条边,如果创建每条边都进行一次数据库查询,可以想见其时间消耗会极为恐怖。为了避免这种情况的发生,我们要对查询进行合并;
为此,我定义了一个权重类:
public class Weight
{
const double infinitesimal = 1e-100;
double Cinfinitesimal = CalculateWeight(infinitesimal);
/**
* 保存统计概率
*/
public double trueWeight = 0;
/**
* 保存取自然对数后的转移概率
*/
public double calculateWeight = 0;
/**
* 以下两个对象是后备的转移概率;
* 假使不存在关于“我 们”这一2元组的统计概率,则尝试取“我 ”的统计概率,
* 若无,则再尝试取“ 们”的统计概率,若还无,则返回1e-100;
*/
public Weight nextWeight1;
public Weight nextWeight2;
/**
* 标记该对象有无被设置过
*/
bool isSet = false;
public double TrueWeight
{
get
{
if (!isSet)
{
if (nextWeight1 != null)
{
return nextWeight1.TrueWeight;
}
else if (nextWeight2 != null)
{
return nextWeight2.TrueWeight;
}
return infinitesimal;
}
return trueWeight;
}
}
public Weight()
{
}
public virtual double value()
{
if (!isSet)
{
if (nextWeight1 != null)
{
return nextWeight1.value();
}
else if (nextWeight2 != null)
{
return nextWeight2.value();
}
return Cinfinitesimal;
}
return calculateWeight;
}
public Weight setValue(double weight)
{
isSet = true;
nextWeight1 = null;//该对象有值,无必要保持后备
nextWeight2 = null;
this.trueWeight = weight;
calculateWeight = CalculateWeight(weight);
return this;
}
protected static double CalculateWeight(double weight)
{
return Math.Log(weight);
}
}
而对于从一个词组到某个词组的转移概率的计算还要稍微更复杂一些;
这里定义一个BiWeight类:
public class BiWeight : Weight
{
Weight delta;
/**
* 避免重复计算
*/
Boolean isDone = false;
public BiWeight(Weight w1, Weight w2, Weight delta) : base()
{
this.nextWeight1 = w1;
this.nextWeight2 = w2;
this.delta = delta;
}
public override double value()
{
if (!isDone)
{
trueWeight = nextWeight1.TrueWeight * nextWeight2.TrueWeight * (Math.E + delta.TrueWeight);
calculateWeight = CalculateWeight(trueWeight);
}
return calculateWeight;
}
}
此处的公式与我们之前的统计模型中转移概率的计算方法是稍有出入的,这可能与实际统计模型的训练方法有关,我可以给出解释的部分是为什么要加一个自然对数e。就是当两个词组之间的转移概率非常小的时候(从Weight的定义中我们可以知道是1e-100),那整条路径的求解结果就会因此都变得非常小,而使路径作废,加入自然对数e可以起到平滑之效。所以事实上你也可以将其换成1或者2,但是我实验的结果是,用e效果最好。不得不说的是,e确实是一个很神奇的数字。
处理合并查询的类是ProbabilityLib,这个类中的代码稍微多一些,我对其进行分块讲解;其所包含的成员如下:
const double infinitesimal = 1e-100;
const string unknown = "";
Dictionary weights = new Dictionary();
Dictionary unknownWeights = new Dictionary();
两个常量我们后面会用到,不多解释;
weights对象是用于保存已查询的转移概率的字典,其道理也是基于用户输入的渐进性特点。其键的类型为long,我们将使用字符串的哈希值作为键值;
unknownWeights对象是用于保存未知的待查询的转移概率的字典。
当我们向数据库查询一个一元数据时:
internal Weight GetUnigram(string phrase)
{
long key = hashCode(phrase);
if (!weights.ContainsKey(key))
{
if (!unknownWeights.ContainsKey(key))
{
var w = new Weight();
unknownWeights.Add(key, w);
return w;
}
else
{
return unknownWeights[key];
}
}
else
{
return weights[key];
}
}
这里所使用的hashCode方法和我们前面对数据库进行哈希化的方法是一样的,否则就无法将数据正确的对应起来。
如果一元数据的转移概率已知,则返回相应的对象;
如果未知,则放入unknownWeights中备查,并返回相应的对象;
当我们向数据库查询一个二元数据时,与查询一元时是类似的,只不过稍微繁复一些而已,最后返回的是一个BiWeight类,利用的是面向对象的多态特性;
internal Weight GetBigram(string prev_phrase, string succ_phrase)
{
long key = hashCode(prev_phrase + " " + succ_phrase);
Weight delta;
List list = new List();
if (!weights.ContainsKey(key))
{
if (!unknownWeights.ContainsKey(key))
{
delta = new Weight();
unknownWeights.Add(key, delta);
long key2 = hashCode(prev_phrase + " " + unknown);//添加后备转移概率1
if (!weights.ContainsKey(key2))
{
if (!unknownWeights.ContainsKey(key2))
{
var w2 = new Weight();
delta.nextWeight1 = w2;
unknownWeights.Add(key2, w2);
}
else
{
delta.nextWeight1 = unknownWeights[key2];
}
}
else
{
delta.nextWeight1 = weights[key2];
}
long key3 = hashCode(unknown + " " + succ_phrase);//添加后备转移概率2
if (!weights.ContainsKey(key3))
{
if (!unknownWeights.ContainsKey(key3))
{
var w3 = new Weight();
delta.nextWeight2 = w3;
unknownWeights.Add(key3, w3);
}
else
{
delta.nextWeight2 = unknownWeights[key3];
}
}
else
{
delta.nextWeight2 = weights[key3];
}
}
else
{
delta = unknownWeights[key];
}
}
else
{
delta = weights[key];
}
return new BiWeight(GetUnigram(prev_phrase), GetUnigram(succ_phrase), delta);
}
现在所有需要查询的转移概率都已经被收集起来,该是一并解决他们的时候了。
public void dealUnknownWeights()
{
var array = unknownWeights.ToArray();
StringBuilder s = new StringBuilder("select * from hashtable where ");
bool done = false;
for (int i = 0; i < array.Length;)
{
if (done)
{
s.Append(" or ");
}
done = true;
s.Append("hashcode = " + array[i++].Key);
if (i % 998 == 0)//一次查询不能超过1000个,只能分段查询;
{
s.Append(";");
done = false;
getProbability(s);
s = new StringBuilder("select * from hashtable where ");
}
}
if (array.Length % 998 != 0)
{
s.Append(";");
getProbability(s);
}
//最后将经过处理的Weight对象都放入weights中,表示其值已知,无论有没有被查询到;
foreach (var i in unknownWeights)
{
weights.Add(i.Key, i.Value);
}
unknownWeights.Clear();
}
void getProbability(StringBuilder s)
{
var list = DataBase.Query(s.ToString());
foreach (var v in list)
{
var w = unknownWeights[v.HashCode];
w.setValue(v.Probability);
}
}
其中,DataBase是链接到哈希化之后的数据文件的对象。
由于边持有对Weight对象的引用,其权重的值都已自动更新好了,不必再重新映射;
完成这一步之后,整个词组图才算构建完全。
求最短路径
现在,我们只要求解词组图中从(S)到(T)的最短路径,即可知该拼音序列下最可能的句子。
郭所使用的算法是动态规划,其优点是可以求解最短的K条路径,但计算量比较大。考虑到实际使用中,我只需要一条整句结果,那么目标应该是以最快的速度求解最短路径,因此我换了另一种算法——基于拓扑排序的最短路径算法;
这个算法分两步,首先是对图的顶点进行拓扑排序:
public class DepthFirstOrder {
bool[] marked;
Stack reversePost;
public DepthFirstOrder(Graph G) {
reversePost = new Stack();
marked = new bool[G.Vertexes.Length];
for (int i = 0; i < G.Vertexes.Length; i++) {
if (!marked[i]) dfs(G, i);
}
}
public Stack ReversePost { get { return reversePost; } }
private void dfs(Graph g, int v) {
marked[v] = true;
foreach (var i in g.adj(v)) {
if (!marked[i]) dfs(g, i);
}
reversePost.Push(v);
}
}
这其实就在对图进行深度优先遍历时将先返回的顶点压入栈;
第二步是按照拓扑排序的结果对图中的顶点依次执行“放松”操作;
public class AcyclicSP
{
Graph.Edge[] edgeTo;
double[] distTo;
public AcyclicSP(Graph g, int s)
{
edgeTo = new Graph.Edge[g.Vertexes.Length];
distTo = new double[g.Vertexes.Length];
for (int v = 0; v < g.Vertexes.Length; v++)
{
distTo[v] = double.PositiveInfinity;
}
distTo[s] = 0;
DepthFirstOrder order = new DepthFirstOrder(g);//拓扑排序
foreach (var v in order.ReversePost)
{
relax(g, v);
}
}
/**
* 这就是所谓的放松操作
*/
private void relax(Graph g, int v)
{
foreach (var e in g.adjEdge(v))
{
int w = g.getIndex(e.to);
var v2 = (e.data as SLMGraph.EdgeData).weight.value();
double v1 = distTo[v] - v2;//此处使用负号,是对求自然对数后的转移概率取反,使其变成正数;
if (distTo[w] > v1)
{
distTo[w] = v1;
edgeTo[w] = e;
}
}
}
/**
* 输出最短路径上的顶点
*/
public Stack pathTo(Graph g, int v)
{
Stack path = new Stack();
bool done = false;
for (var e = edgeTo[v]; e != null; e = edgeTo[g.getIndex(e.from)])
{
if (done) path.Push(e);
done = true;
}
return path;
}
}
至于这个算法为什么可以求解最短路径,超出了我的能力范畴,请感兴趣的朋友参阅《算法》一书。
该算法的特点是只能求解有向加权无环图的最短路径,而词组图是天生的有向加权无环图。
按照拓扑顺序放松顶点,就能在和E+V成正比的时间内解决无环加权有向图的单点最短路径问题。
在已知加权图是无环的情况下,它是找出最短路径的最好方法。 ——《算法》
模型整合与实验
所有“物料”齐备后,我们应该将其整合到一起方便使用:
public class SuiHan2GramModel {
private string sentence;
public SuiHan2GramModel(string sheng, string yun) {
LexiconGraph graph = new LexiconGraph(sheng, yun);
SLMGraph sgraph = new SLMGraph(graph);
AcyclicSP sp = new AcyclicSP(sgraph, 0);
var path = sp.pathTo(sgraph, sgraph.VertexCount - 1);
StringBuilder s = new StringBuilder();
foreach (var i in path) {
s.Append(i.to.ToString());
}
sentence = s.ToString();
}
public string Sentence {
get {
return sentence;
}
}
}
我们用下述代码,测试这个整句模型的性能:
static void makeSentence(string sheng, string yun)
{
Stopwatch s = new Stopwatch();
s.Start();
var gram = new SuiHan2GramModel(sheng, yun);
s.Stop();
Console.WriteLine(gram.Sentence + s.ElapsedMilliseconds);
}
public static void Main(string[] args)
{
//在此之前应当执行初始数据库的操作
makeSentence("wmydydbsyddr", "oIiPFaDX4eiI");
}
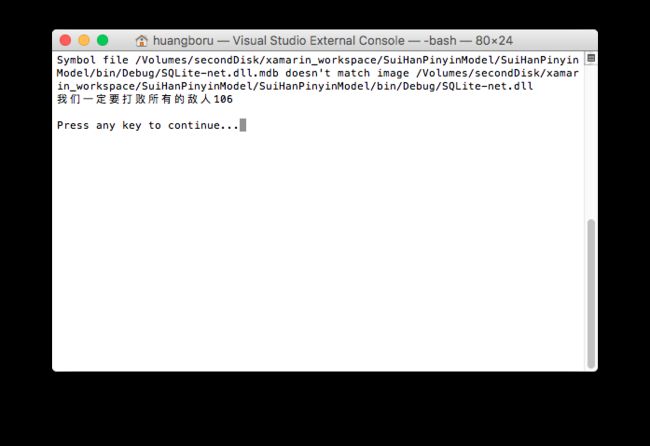
实验结果如下:
106ms的运行时间还是有点长的,但是请注意,这里我们并没有引入用户的输入渐进性,而是直接对整个拼音序列执行整句,所以我们应当模仿用户实际输入的渐进过程再做次实验。
public static void Main(string[] args)
{
const string sheng = "wmydydbsyddr";
const string yun = "oIiPFaDX4eiI";
for (int i = 1; i <= sheng.Length; i++)
{
makeSentence(sheng.Substring(0, i), yun.Substring(0, i));
}
}
实验结果:
9ms!应该说是非常不错的成绩,用时最长的反而是查询最短的时候,说明此时初始化的开销成为了整句过程的大头,也充分说明了对词组查询和概率查询的缓存的重要性。一个10ms级的整句引擎理论上是不会导致用户在输入时出现卡滞现象的,已经可以满足实用需要了。
如果我们再削减取词的数量,可以将时间开销控制得更低,但是必须与整句的正确性之间取得平衡。
要点回顾
我简单回顾一下,整句引擎开发之中的优化要点:
- 统计数据的哈希化
- 建立unique索引
- 对取词进行排序并限制取词的数量
- 对取词进行缓存,以利用实际输入过程的渐进性
- 对概率查询进行合并
- 对概率查询进行缓存,以利用实际输入过程的渐进性
- 使用拓扑排序求解最短路径
写在最后
我之前认为实现一个整句引擎,起码要使用C/C++这个级别的语言,在开发这个整句引擎之前,我一直担心其性能无法满足需求。但事实证明,只要优化得当,使用C#是可以实现一个10ms级的整句引擎的(同理,java应该也可以)。
如果你想将这个引擎应用到其它形式的输入法中,比如形码输入法,是可以的,只需要正确改写LexiconGraph类和LexiconLib类即可。
至于这套整句引擎的全套代码,因为事实上我在文中已经和盘托出了,并且对所有的技术细节都做了讲解,我相信按照这套路做下来,你也可以实现一个与我如出一辙的整句引擎,所以我也就没有必要开源这套引擎的代码了。当然,有一部分的原因是这套引擎引用了岁寒输入法的某些模块,开源这套引擎也就意味着这部分模块也要开源才行。
文中提及的两本书——《数学之美》和《算法》也是强烈向大家推荐的。
最后,还打一剂广告吧,不管是不是违法广告法了。