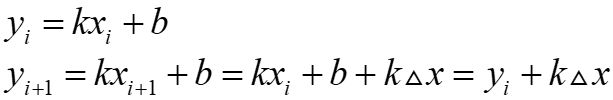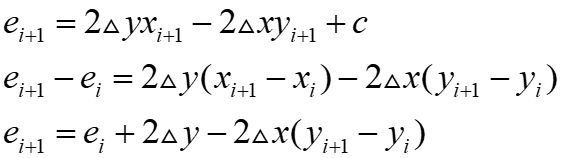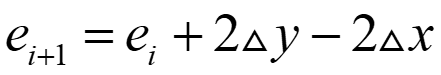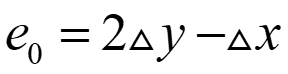图形学入门(1)——直线生成算法（DDA和Bresenham）

开一个新坑，记录从零开始学习图形学的过程，现在还是个正在学习的萌新，写的不好请见谅。

 

首先从最基础的直线生成算法开始，当我们要在屏幕上画一条直线时，由于屏幕由一个个像素组成，所以实际上计算机显示的直线是由一些像素点近似组成的，直线生成算法解决的是如何选择最佳的一组像素来显示直线的问题。

对这个问题，首先想到的最暴力的方法当然是从直线起点开始令x或y每次增加1直到终点，每次根据直线方程计算对应的函数值再四舍五入取整，即可找到一个对应的像素，但这样做每一步都要进行浮点数乘法运算，效率极低，所以出现了DDA和Bresenham两种直线生成算法。

 

一，数值微分法（DDA算法）

DDA算法主要是利用了增量的思想，通过同时对x和y各增加一个小增量，计算下一步的x和y值。

 

 

根据上式可知$\bigtriangleup x$=1时，x每递增1，y就递增k，所以只需要对x和y不断递增就可以得到下一点的函数值，这样避免了对每一个像素都使用直线方程来计算，消除了浮点数乘法运算。

代码实现：

 

#include
#include
#include
using namespace std;

const int ScreenWidth = 500;
const int ScreenHeight = 500;

LRESULT CALLBACK WinProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)
{
    switch (message) {
    case WM_CLOSE:
        DestroyWindow(hWnd);
        break;
    case WM_DESTROY:
        PostQuitMessage(0);
        break;
    default:
        return DefWindowProc(hWnd, message, wParam, lParam);
        break;
    }
    return 0;
}

void DDALine(int x0,int y0,int x1,int y1,HDC hdc)
{
    int i=1;
    float dx, dy, length, x, y;
    if (fabs(x1 - x0) >= fabs(y1 - y0))
        length = fabs(x1 - x0);
    else
        length = fabs(y1 - y0);
    dx = (x1 - x0) / length;
    dy = (y1 - y0) / length;
    x = x0;
    y = y0;
    while (i<=length)
    {
        SetPixel(hdc,int(x + 0.5), ScreenHeight-40-int(y + 0.5), RGB(0, 0, 0));
        x = x + dx;
        y = y + dy;
        i++;
    }
}
int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance, PSTR szCmdLine, int nShowCmd)
{
    WNDCLASS wcs;
    wcs.cbClsExtra = 0;                                         // 窗口类附加参数  
    wcs.cbWndExtra = 0;                                         // 窗口附加参数  
    wcs.hbrBackground = (HBRUSH)GetStockObject(WHITE_BRUSH);    // 窗口DC背景  
    wcs.hCursor = LoadCursor(hInstance, IDC_CROSS);             // 鼠标样式  
    wcs.hIcon = LoadIcon(NULL, IDI_WINLOGO);                    // 窗口icon  
    wcs.hInstance = hInstance;                                  // 应用程序实例  
    wcs.lpfnWndProc = (WNDPROC)WinProc;
    wcs.lpszClassName = "CG";
    wcs.lpszMenuName = NULL;
    wcs.style = CS_VREDRAW | CS_HREDRAW;
    RegisterClass(&wcs);
    HWND hWnd;
    hWnd = CreateWindow("CG","DrawLine", WS_OVERLAPPEDWINDOW, 200, 200, ScreenWidth, ScreenHeight, NULL, NULL, hInstance, NULL);
    ShowWindow(hWnd, nShowCmd);
    UpdateWindow(hWnd);
    MSG msg;

    // hdc init
    HDC hdc = GetDC(hWnd);

    // 绘图，画一条从点（0,0）到（100,350）的直线
    DDALine(0, 0, 100, 350, hdc);// 消息循环  
    while (GetMessage(&msg, 0, NULL, NULL)) {
        TranslateMessage(&msg);
        DispatchMessage(&msg);
    }

    // release
    ReleaseDC(hWnd, hdc);
    return 0;
}

 

 

以上是DDA算法的实现，WinMain和WinProc函数是Windows API编程特有的，我们只需要关注DDALine这个绘图函数，该函数传入两个点的坐标画出一条直线。

首先判断起点和终点间x轴和y轴哪个轴向的跨度更大（斜率范围），为了防止丢失像素，应让跨度更大的轴向每次自增1，这样能获得更精确的结果。

接下来就没什么好说的，依次让x和y加上增量然后四舍五入就行了，浮点数四舍五入可以直接用int(x+0.5)计算，setPixel函数用于设置像素的颜色值（需要传入窗口的hdc句柄），由于Windows窗口坐标的原点在左上角，所以拿窗口高度减去y值就可以转换成平常习惯的左下角坐标系了。

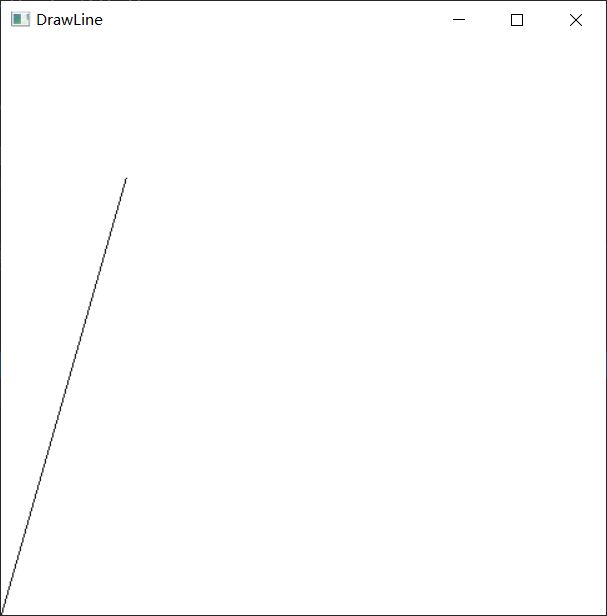
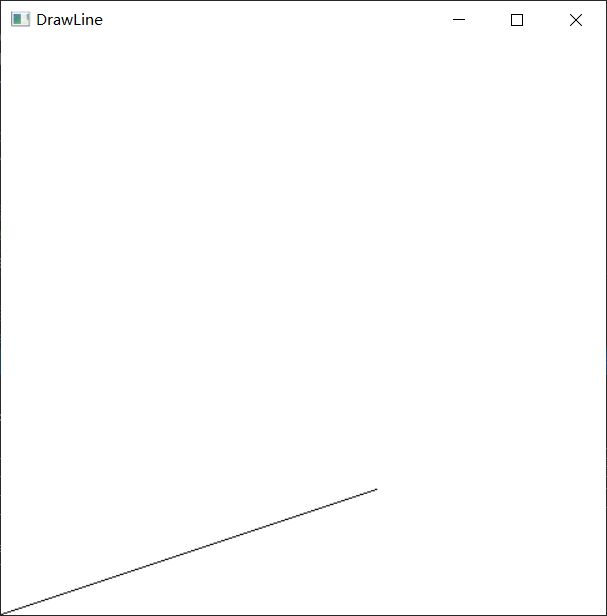
运行结果:

 

 

 

 

  

二，Bresenham算法

DDA算法尽管消除了浮点数乘法运算，但仍存在浮点数加法和取整操作，效率仍有待提高，1965年Bresenham提出了更好的直线生成算法，成为了时至今日图形学领域使用最广泛的直线生成算法，该算法采用增量计算，借助一个误差量的符号确定下一个像素点的位置，该算法中不存在浮点数，只有整数运算，大大提高了运行效率。

 我们先只考虑斜率在0-1之间的情况，从线段左端点开始处理，并逐步处理每个后续列，每确定当前列的像素坐标$(x_{i},y_{i})$后，那么下一步需要在列$x_{i+1}$上确定y的值，此时y值要么不变，要么增加1，这是因为斜率在0-1之间，x增长比y快，所以x每增加1，y的增量是小于1的。

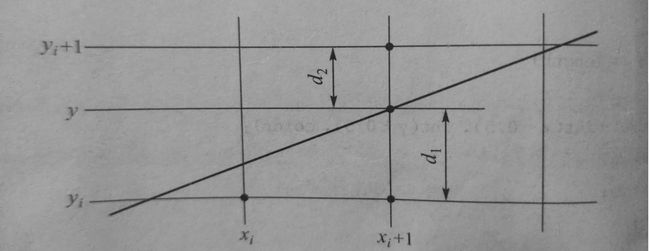
对于左端点默认为其像素坐标，下一列要么是右方的像素，要么是右上方的像素，设右上方像素到直线的距离为d2，右方像素到直线的距离为d1，显然只需要判断直线离哪个像素点更近也就是d1-d2的符号即可找到最佳像素。

 

 所以可以推出以下式子：

 

 其中$\bigtriangleup x$起点到终点x轴上距离，$\bigtriangleup y$为y轴上距离，k=$\bigtriangleup y$/$\bigtriangleup x$，c是常量，与像素位置无关。

令$e_{i}$=$\bigtriangleup x$(d1-d2),则$e_{i}$的计算仅包括整数运算，符号与d1-d2一致，称为误差量参数，当它小于0时，直线更接近右方像素，大于0时直线更接近右上方像素。

可利用递增整数运算得到后继误差量参数，计算如下：

 

 所以选择右上方像素时($y_{i+1}$-$y_{i}$=1)：

 

 选择右方像素时($y_{i+1}$-$y_{i}$=0)：

 

 初始时，将k=$\bigtriangleup y$/$\bigtriangleup x$代入$\bigtriangleup x$(d1-d2)中可得到起始像素的第一个参数：

 

斜率在0-1之间的Bresenham算法代码实现（替换上面程序中DDALine即可）：

void Bresenham_Line(int x0, int y0, int x1, int y1, HDC hdc)
{
    int dx, dy, e, x=x0, y=y0;
    dx = x1 - x0; dy = y1 - y0;
    e = 2 * dy - dx;
    while (x<=x1)
    {
        SetPixel(hdc, x, ScreenHeight-40-y, RGB(0, 0, 0));
        if (e >= 0)//选右上方像素
        {
            e = e + 2 * dy - 2 * dx;
            y++;
        }
        else//选右方像素
        {
            e = e + 2 * dy;
        }
        x++;
    }
}

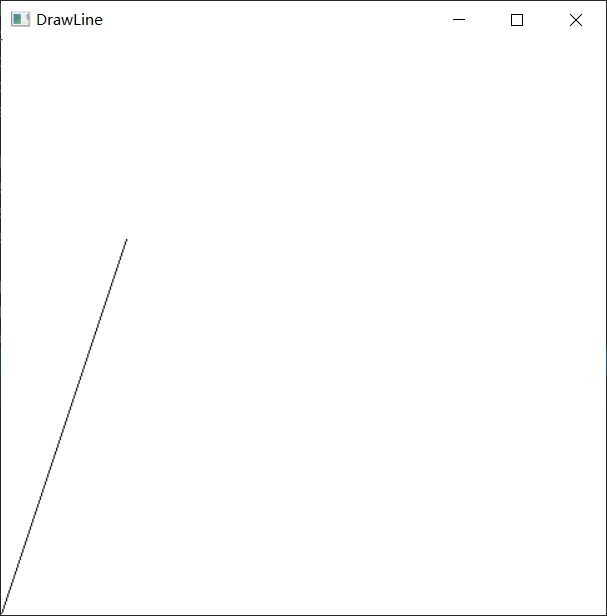
运行结果：

 

 

 

要实现任意方向的Bresenham算法也很容易，斜率在0-1之间意味着直线位于坐标系八象限中的第一象限，如果要绘制第二象限的直线，只需要利用这两个象限关于直线x=y对称的性质即可，可以先将x和y值互换先在第一象限进行计算，然后调用SetPixel时再将x和y值反过来，在第二象限中绘制，其他象限也是类似的思路。

绘制任意方向直线的Bresenham算法代码实现：

void Bresenham_Line(int x0, int y0, int x1, int y1, HDC hdc)
{
    int flag = 0;
    int dx = abs(x1 - x0);
    int dy = abs(y1 - y0);
    if (dx == 0 && dy == 0)   return;
    if (abs(x1 - x0) < abs(y1 - y0))
    {
        flag = 1;
        swap(x0, y0);
        swap(x1, y1);
        swap(dx, dy);
    }
    int tx = (x1 - x0) > 0 ? 1 : -1;
    int ty = (y1 - y0) > 0 ? 1 : -1;
    int x = x0;    
    int y = y0;
    int dS = 2 * dy;   int dT = 2 * (dy - dx);
    int e = dS - dx;
    SetPixel(hdc, x0, y0, RGB(0,0,0));
    while (x != x1)
    {
        if (e < 0)
            e += dS;
        else
        {
            y += ty;  e += dT;
        }
        x += tx;
        if (flag)
            SetPixel(hdc, y, ScreenHeight - 40 - x, RGB(0, 0, 0));
        else
            SetPixel(hdc, x, ScreenHeight - 40 - y, RGB(0, 0, 0));
    }
}

 

 

 

直线生成算法就到这里啦，接下来也要加油学习图形学~