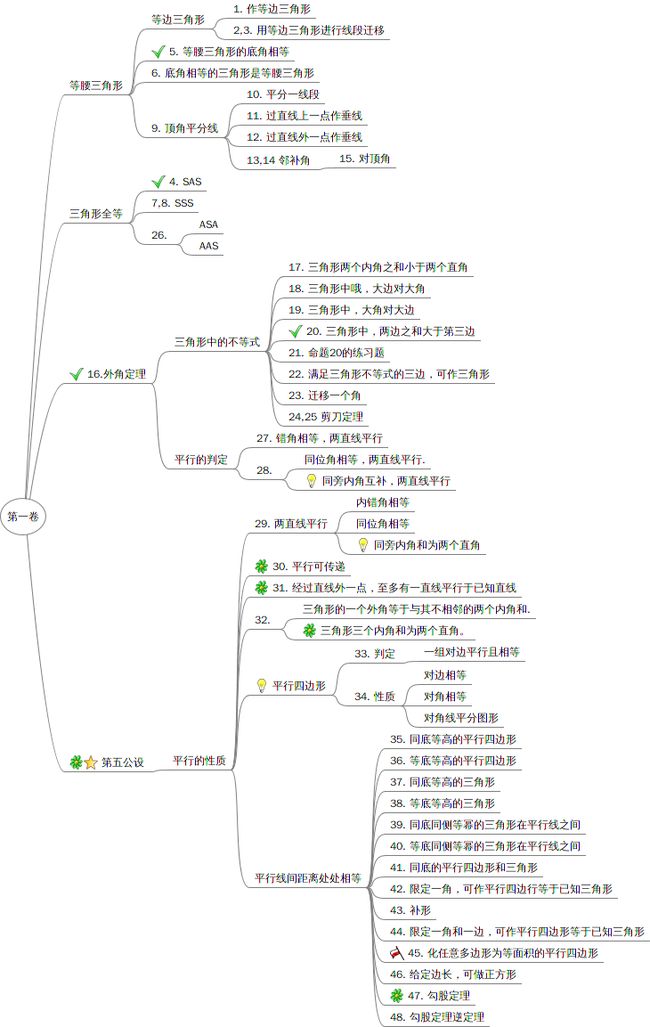
从命题十七开始,到命题三十二为止。探讨三角形中的不等式。同时,也讨论平行。
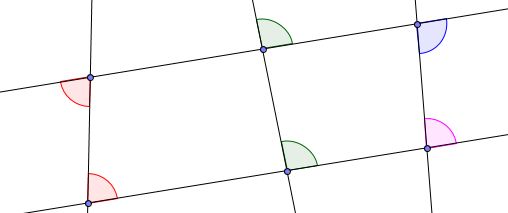
现代的不等号,就是在一组平行线上,画上一条斜线。≠ 。研究平行的时候也是,用一条直线与待考察的两条直线相交,然后考察那些相交的角。不等关系从一开始就与平行有着说不清的联系。就像透过有限,来研究无限;透过相交,来研究平行;知道生,才知道死。这些道理是一致的。
讨论平行的命题,从第二十七开始。但只有二十七,二十八两个命题是来自外角定理的推论。
从第二十九命题开始,第一卷剩下所有的命题都与第五公设相关。
因此,第一卷可以这样划分:
先划分为两部分,
1-28命题为第一部分,得到一条平行线;
29-48命题为第二部分,研究这线的性质。
或者说,独立于第五公设的部分,以及第五公设推导的部分。
≠ 关系
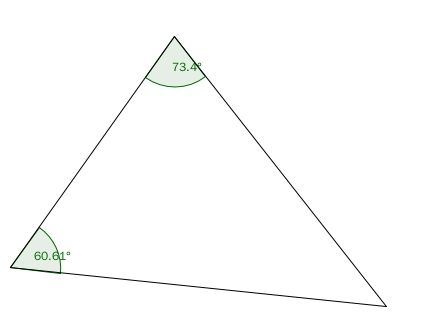
命题十七 三角形的两个内角和小于两直角。
这个命题是外角定理直接的推论,假设三角形的两个内角为A,B,C,而且与A相邻的外角为 alpha,明显,A+alpha为两个直角,而 B< alpha,所以A+B小于两个直角。
作为外角定理的推论,也与外角定理等价。这个命题,比看上去重要,留待后面讨论。
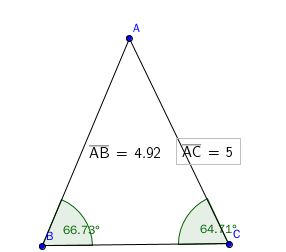
命题十八 在三角形中,大边对大角。
图形只是一个特例。这个命题与第五命题呼应。
命题十九 在三角形中,大角对大边。
命题十九实际上蕴含在命题十八的逆否命题中。“大边对大角”的逆否命题是“不大的角对不大的边”,也就是“等角或小角对等边或小边”,比较的时候,是两个角在比较,一个角自称“等角或小角”,那么另一个角就可自称为“大角”,一个边自称“等边或小边”,那么,另一个边自然是“大边”,那么,从另一个角的和它对的边来看,自然就是“大角对大边”。
而且,这两个命题的排列同前面的都有所不同,例如命题5和命题6,排列上奇数在前,偶数在后。从这两个命题开始,本部分“成对”出现的命题都变成了偶数在前,奇数在后。直到第三部分,讨论面积的时候,恢复成原始的样子。
这里发生了什么?留待后面讨论。
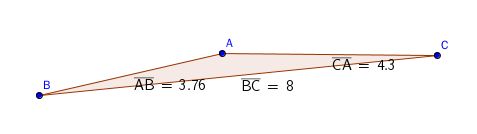
命题二十 三角形两边之和大于第三边。
这个从直觉上,折线长大于线段长就可以理解。或者“两点之间,直线最短”也可以得出解释。
这个是著名的“三角形不等式”。
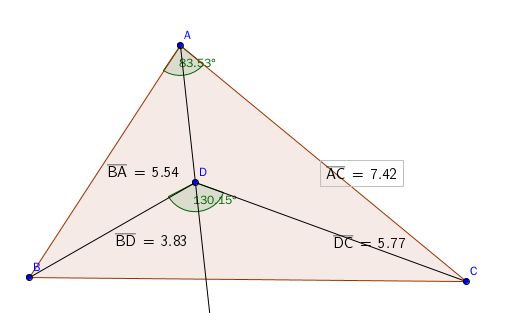
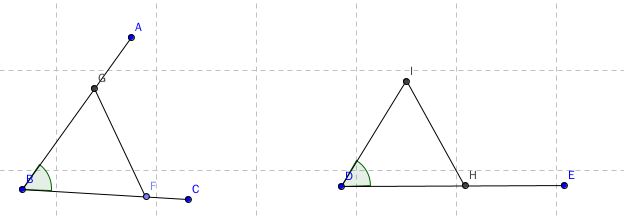
命题二十一 以三角形一边的两个端点向三角形内引两条相交线,那么交点到这两个端点的两条线段和小于三角形余下的两边和,所形成的角大于余下两边的夹角。
这个命题很长。实际上是命题二十的练习题。看起来像是凑数的命题,纯粹为调节命题序号而存在。但与圆内的点相关的命题比较起来看,存在也很合理。
如图的三角形ABC内取一点,连接BD,BC,则角BDC大于角BAC,这个容易证明,因为角BDC可以看作两个三角形的外角。根据外角定理,以及同向不等式可加,易证。
长度的证明有技巧性,因此是及好的练习题。只适当的做辅助线,运用命题20证明。
命题二十二 用满足三角形不等式的三边可作三角形。
这个命题实际上对命题一作出了保证。保证了等边三角形可以做出来。
这个命题实际上是命题二十的逆命题。命题二十讲,如果已知j三角形,那么可以有不等式。本命题是讲,如果同时满足三个不等式,那么可做三角形。
命题二十三 给定顶点和一边,可迁移角。
实际上使用了SSS全等来迁移一个角。希尔伯特对角的迁移作了公理化处理。
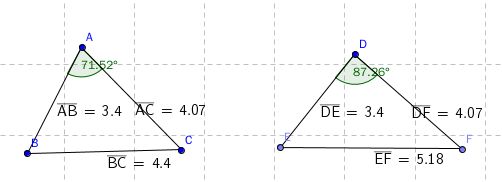
命题二十四 两个三角形有两条边对应相等,其中一个三角形对应的夹角大于另一个三角形的夹角,那么,这个三角形的第三边也大于另一个的第三边。
命题二十五 三角形中如果有两条对应边相等,其中一个的第三边比另一个大,那么,较大的边对的角也较大。
这两个命题被形象的称为“剪刀定理”,好比拿着一把剪刀,两边张开的角度越大,剪刀两个尖端的距离自然越远;反之也是,要剪大的东西,自然要张开更大的角度。
这两个命题实际上是余弦定理的前身,精确量化以后,就是余弦定理。而余弦定理在取直角的时候,就是勾股定理。因此,这两个定理同勾股定理有着联系。也同SAS和SSS全等密切联系。很明显,两旁的量如果一样,那么中间的量决定了三角形是否能够全等。
这两个命题是“成对”的,注意到,仍然是偶数序号在前面。这不科学,好比印书的时候,把页码2,和页码3印在一张纸的正反面。为什么这样呢?留待后面解释。
命题二十六 ASA全等,AAS全等
ASA全等可以通过前面的各种全等证明。也可以出现在更早的地方。欧几里得的证明用到了外角定理,因此出现在这里。希尔伯特因为规定了角的迁移,因此,一早就给出了证明。
ASA出现在这里,表示,
前方高能
要把等腰三角形的两个底角张开来,把腰挺直,让顶角分开,看看,张开到什么程度,腰所在的向上的射线就不再相交。
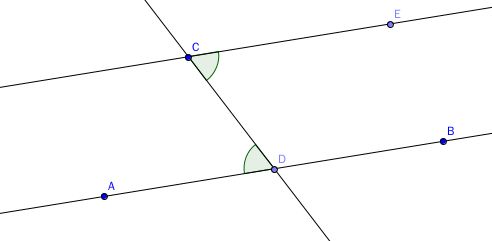
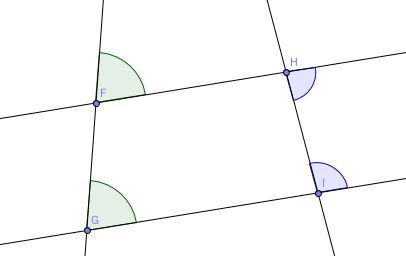
命题二十七 内错角相等,两直线平行。
命题二十八 同位角相等,两直线平行。同旁内角互补,两直线平行。
这两个命题就明确的指出了,直线什么时候不相交,也就是平行。
这两个命题本质上是一样。给出了三种判定平行线的方法。证明过程中,用到了外角定理。也就是说,这两个命题把重要的事情说了三遍。
这两个命题是平行线的判定定理。
这两个命题的来源是命题十六,外角定理。
这里本该安排三个命题,或者一个就够了。为什么是两个呢?仅仅为了调节配对。要做这样的事情,只是因为命题十七。
再次考察命题十七。
三角形的两个内角和小于两直角
欧几里得曾为好看的命题都增加一个逆命题或者配对的命题。但命题十七没有。当初应该有。那么当初,命题十七的逆命题是怎样的呢?
先看原命题
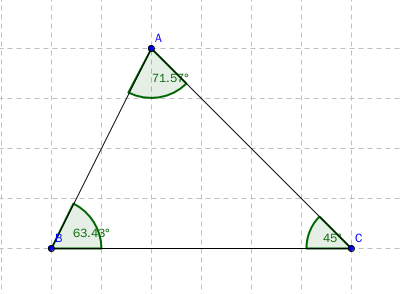
原命题说,如图三角形的两个内角和小于两个直角。
命题十七原命题也可以这样说:
同一平面内,一条直线(AB)和另外两条直线(AC和BC)相交,这两条直线在AB的一侧相交(点C为交点),那么,这一侧的两个内角和小于二直角的和。
那么,当初,命题十七的逆命题或者说配对的命题应该这样写:
同平面内一条直线和另外两条直线都相交,若在直线同侧的两个内角之和小于两个直角,则这两条直线(无限延伸后)在这一侧相交。
眼熟吗?当初,欧几里得每写一个命题,就配对一个命题(有是逆命题,有时不是)。然后证明之。到第十七命题的时候,也配对了这样一个命题。然后就开启了证明模式。
最后发现,尽管这个命题直觉上很正确的,但用已有的全等理论、外角定理等等,居然无法证明!无法证明!无法证明!
于是,他就把本该是第十八命题的这个命题移到前面,悬挂在那里,暂时作为公设,有空了回来证证看。后面几个命题序号的奇偶先错乱一下,算是作个标记,提醒自己回来证明这个公设。
现有的命题十八和命题十九互为逆否命题,也暗示了这一点。也就是说。命题十八和命题十九是完全等价的。因此,可以只有一个。
因为一直不能证明,所以它就一直不能回到命题十八的位置上,而只能一直悬挂在前面,作为公设永远流传下来了。
这个公设就是第五公设。引无数英雄竞折腰。欧几里得是第一个英雄,后面还有很多很多的英雄,试图用第一到第十七命题来证明它,但从来没有成功过。
如果你也想尝试一下,那么,一定只能用最前面的十七个命题,或者宽一点,第一卷最前面的二十八个命题。因为,假如用了后面的命题,一不小心就会使用第五公设的等价命题来证明第五公设。就像证明“我是我”一样,因为“我是我”,所以“我是我”。
第五公设引出的故事,用三天三夜也讲不完。
命题二十九 两直线平行,内错角相等,同位角相等,同旁内角互补(和为两个直角)。
命题二十九是命题二十七和二十八的逆命题。证明的时候,不得已要用到第五公设。
这个命题讲的是平行线的性质,也就是已知两直线平行,会发生什么。
这个命题的证明用到了第五公设。
并且,从这个命题开始,直到第48命题,每一个都同第五公设有关。因为,用到了平行线的性质。
因此,凡是不得不使用平行线性质证明的命题,都需要第五公设直接或间接来参与证明。
第二十七和二十八命题讲平行线的判定,也就是说,判定两两直线满足某些条件,就可以平行。来源是外角定理,与第五公设无关。
命题三十 一些直线平行于同一直线,它们也相互平行。
这是平行的传递性。也属于平行线的性质。自然,与第五公设相关。实际上,等价。
命题三十一 Playfair公理
尽管有人不认为欧几里得发现了这个公理,过直线外一点,能作且只能作一条平行线平行于已知直线。但我认为,他肯定知晓。因为,这个命题的位置在这里。它前后的命题都与第五公设相关,它自身也是与第五公设相关的。
单从外角定理就可以做平行线了,例如,平移正三角形的一内角到外角内。证明平行不需要第五公设。
欧几里得单独设这样一个命题,就是在说:只能作一条平行线。
既然第五公设放在了前面,这个等价的命题就没有必要也放在前面。
命题三十二 三角形的一个外角等于与其不相邻的两个内角之和。三角形的三个内角和为两个直角。
这个命题,是三角形的内角和定理。最广为人知。
三角形三个内角的和为一百八十度。
证明的时候,直接使用了平行线的性质。
也可以用来代替第五公设。
用平行线的性质,很容易证明平行线之间,处处距离相等。
勾股定理也就有了基础。
同时,勾股定理与第五公设也有密切的关系。
在此后,很多地方,如相似等,都用的了平行线的性质,也就是说,间接引用了第五公设。第五公设看上去很长,望之不似人君,所以,后来的数学家想把它证明,然后移除,于是发生很多很多的故事。
第五公设不是家丑,而是欧氏几何的精华。
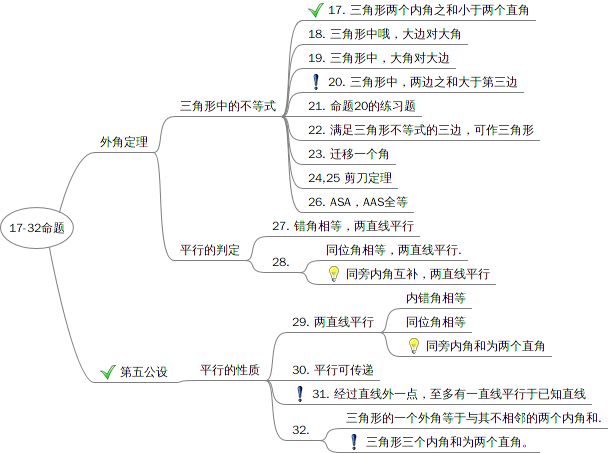
本部分命题结构如下
很多一部分是来自外角定理的命题,只讲三角形中的不等式。
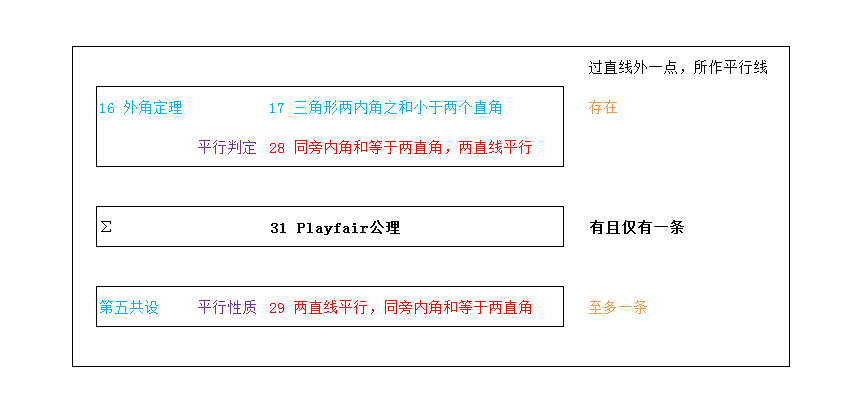
简化结构以后,就是这个样子:
可以看到,第五公设就是命题十七的逆命题,命题28和29也互为逆命题,而且偶数在前。从27到29的命题,可以随意的拆分,调节序号。
30和32命题直接来源于第五公设。
31命题,指出了平行线的存在性,来自外角定理;同时指出了平行线的唯一性,来自第五公设。是两个命题合并起来的命题。
在外角定理作为大前提的情况下,Playfair公理和第五公设是等价的。历史上的英雄想通过证明来移除第五公设的尝试失败了,但成功的帮它完成了瘦身,如今,教科书上都写平行公理:
平行公理(Playfair公理)
给定一条直线,通过此直线外的任何一点,有且仅有一条直线与之平行。
而第五公设的等价写法是
欧几里得公理
设a是任一直线,A是a外的任一点,在a和A所决定的平面上,至多有一条直线过A且不和a相交。
在设定阿基米德公理的情况下,
外角定理表明,存在;
欧几里得公理表明至多有一条。
平行公理说,有且仅有一条。
到底有多少,你说了算。
先师欧几里得,罗巴切夫斯基,黎曼......请赐我力量,让我进步。
最终总结,本卷结构: