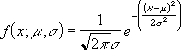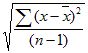上次给大家分享了《2017年最全的excel函数大全13—兼容函数(中)》,这次分享给大家兼容性函数(下),如果你使用的是 Excel 2007,则可以在“公式”选项卡上的统计或数学与三角函数类别中找到这些函数。
MODE 函数
描述
假设您要查找的注册优惠种类注册优惠计数在湿地 30 年时间段的案例中的最常见的数量,或者您想要关闭 pea 期间找出的电话呼叫的电话支持中心出现频率最高的数k 小时。若要计算一组数的数字模式,请使用 MODE 函数。
MODE 返回的数组或数据区域中出现频率最高或重复出现值。
有关新函数的详细信息,请参考MODE.MULT 函数和MODE.SNGL 函数。
用法
MODE(number1,[number2],...)
MODE 函数用法具有下列参数:
Number1必需。要计算其众数的第一个数字参数。
Number2,...可选。要计算其众数的 2 到 255 个数字参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
备注
参数可以是数字或者是包含数字的名称、数组或引用。
如果数组或引用参数包含文本、逻辑值或空白单元格,则这些值将被忽略;但包含零值的单元格将计算在内。
如果参数为错误值或为不能转换为数字的文本,将会导致错误。
如果数据集合中不包含重复的数据点,则 MODE 返回错误值 #N/A。
MODE 函数用于度量集中趋势,集中趋势在统计分步中是一组数字的中心位置。最常用的集中趋势度量方式有以下三种:
平均值平均值是算术平均数,由一组数相加然后除以这些数的个数计算得出。 例如,2、3、3、5、7 和 10 的平均值为 30 除以 6,即 5。
中值中值是一组数中间位置的数;即一半数的值比中值大,另一半数的值比中值小。 例如,2、3、3、5、7 和 10 的中值是 4。
众数众数是一组数中最常出现的数。 例如,2、3、3、5、7 和 10 的众数是 3。
对于对称分布的一组数来说,这三种集中趋势的度量是相同的。 对于偏态分布的一组数来说,这三种集中趋势的度量可能不同。
案例
NEGBINOMDIST 函数
描述
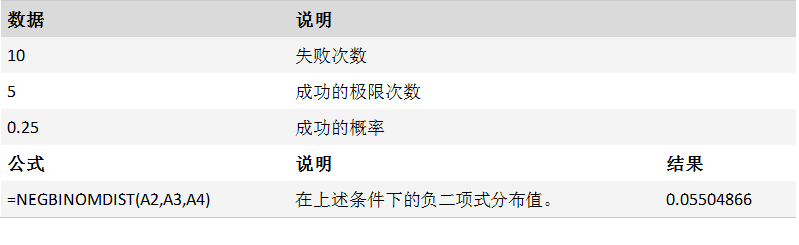
返回负二项式分布。 当成功概率为常量 probability_s 时,NEGBINOMDIST 返回在达到 number_s 次成功之前,出现 number_f 次失败的概率。 此函数与二项式分布相似,只是它的成功次数固定,试验次数为变量。 与二项式分布相同的是,二者均假定试验是独立的。
例如,如果要找 10 个反应敏捷的人,且已知候选人符合相关条件的概率为 0.3。 NEGBINOMDIST 将计算出在找到 10 个合格候选人之前,需面试特定数目的不合格候选人的概率。
有关新函数的详细信息,请参考NEGBINOM.DIST 函数。
用法
NEGBINOMDIST(number_f,number_s,probability_s)
NEGBINOMDIST 函数用法具有下列参数:
Number_f必需。 失败的次数。
Number_s必需。 成功次数的阈值。
Probability_s必需。 成功的概率。
备注
Number_f 和 number_s 将被截尾取整。
如果任一参数为非数值型,则 NEGBINOMDIST 返回 错误值 #VALUE!。
如果 probability_s < 0 或 probability > 1,则 NEGBINOMDIST 返回 错误值 #NUM!。
如果 number_f < 0 或 number_s < 1,则 NEGBINOMDIST 返回 错误值 #NUM!。
负二项式分布的公式为:
其中:
x 是 number_f,r 是 number_s,且 p 是 probability_s。
案例
NORMDIST 函数
描述
返回指定平均值和标准偏差的正态分布函数。 此函数在统计方面应用范围广泛(包括假设检验)。
有关新函数的详细信息,请参考NORM.DIST 函数。
用法
NORMDIST(x,mean,standard_dev,cumulative)
NORMDIST 函数用法具有下列参数:
X必需。 需要计算其分布的数值。
Mean必需。 分布的算术平均值。
standard_dev必需。 分布的标准偏差。
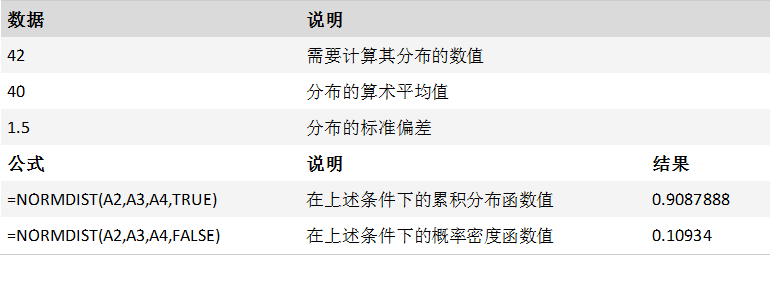
cumulative必需。 决定函数形式的逻辑值。 如果 cumulative 为 TRUE,则 NORMDIST 返回累积分布函数;如果为 FALSE,则返回概率密度函数。
备注
如果 mean 或 standard_dev 是非数值的,则 NORMDIST 返回 错误值 #VALUE!。
如果 standard_dev ≤ 0,则 NORMDIST 返回 错误值 #NUM!。
如果 mean = 0、standard_dev = 1,且 cumulative = TRUE,则 NORMDIST 返回标准正态分布,即 NORMSDIST。
正态分布密度函数 (cumulative = FALSE) 的公式为:
如果 cumulative = TRUE,则公式为从负无穷大到公式中已知的 X 的积分。
案例
NORMINV 函数
描述
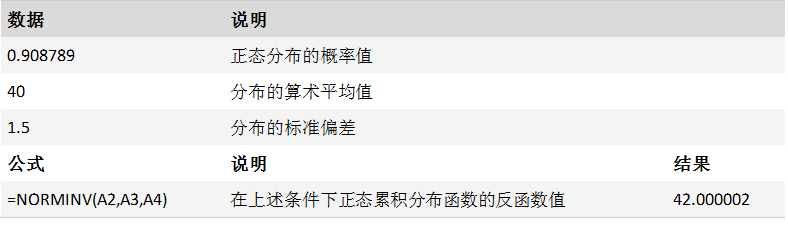
返回指定平均值和标准偏差的正态累积分布函数的反函数值。
有关新函数的详细信息,请参考NORM.INV 函数。
用法
NORMINV(probability,mean,standard_dev)
NORMINV 函数用法具有下列参数:
Probability必需。 对应于正态分布的概率。
Mean必需。 分布的算术平均值。
standard_dev必需。 分布的标准偏差。
其他
如果任一参数为非数值型,则 NORMINV 返回 错误值 #VALUE!。
如果 probability <= 0 或 probability >= 1,则 NORMINV 返回 错误值 #NUM!。
如果 standard_dev ≤ 0,则 NORMINV 返回 错误值 #NUM!。
如果 mean = 0 且 standard_dev = 1,则 NORMINV 使用标准正态分布(请参考 NORMSINV)。
如果已给定概率值,则 NORMINV 使用 NORMDIST(x, mean, standard_dev, TRUE) = probability 求解数值 x。 因此,NORMINV 的精度取决于 NORMDIST 的精度。 NORMINV 使用迭代搜索技术。 如果搜索在 100 次迭代之后没有收敛,则函数返回错误值 #N/A。
案例
NORMSDIST 函数
描述
返回标准正态累积分布函数的函数值。 该分布的平均值为 0(零),标准偏差为 1。 可以使用此函数代替标准正态曲线面积表。
有关新函数的详细信息,请参考NORM.S.DIST 函数。
用法
NORMSDIST(z)
NORMSDIST 函数用法具有以下参数:
Z必需。 需要计算其分布的数值。
其他
如果 z 是非数值的,则 NORMSDIST 返回 错误值 #VALUE!。
标准正态分布密度函数的公式为:
案例
NORMSINV 函数
描述
返回标准正态累积分布函数的反函数值。 该分布的平均值为 0,标准偏差为 1。
有关新函数的详细信息,请参考NORM.S.INV 函数。
用法
NORMSINV(probability)
NORMSINV 函数用法具有下列参数:
Probability必需。 对应于正态分布的概率。
备注
如果 Probability 是非数值的,则 NORMSINV 返回 错误值 #VALUE!。
如果 Probability <= 0 或 Probability >= 1,则 NORMSINV 返回 错误值 #NUM!。
如果已给定概率值,则 NORMSINV 使用 NORMSDIST(z) = probability 求解数值 z。 因此,NORMSINV 的精度取决于 NORMSDIST 的精度。 NORMSINV 使用迭代搜索技术。 如果搜索在 100 次迭代之后没有收敛,则函数返回错误值 #N/A。
案例
PERCENTILE 函数
描述
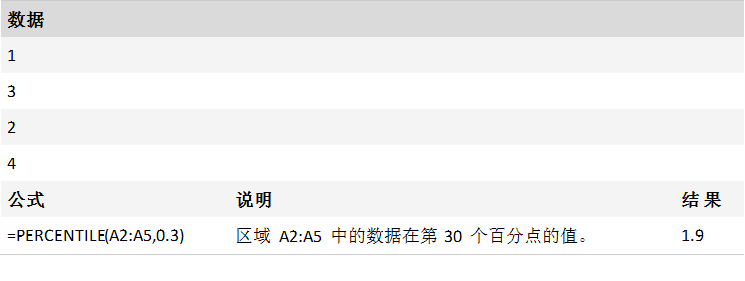
返回区域中数值的第 k 个百分点的值。 可以使用此函数来确定接受的阈值。 例如,可以决定检查得分高于第 90 个百分点的候选人。
有关新函数的详细信息,请参考PERCENTILE.EXC 函数和PERCENTILE.INC 函数。
用法
PERCENTILE(array,k)
PERCENTILE 函数用法具有下列参数:
Array必需。定义相对位置的数组或数据区域。
K必需。 0 到 1 之间的百分点值,包含 0 和 1。
备注
如果 k 为非数值型,则 PERCENTILE 返回 错误值 #VALUE!。
如果 k < 0 或 k > 1,则 PERCENTILE 返回 错误值 #NUM!。
如果 k 不是 1/(n-1) 的倍数,函数 PERCENTILE 使用插值法来确定第 k 个百分点的值。
案例
PERCENTRANK 函数
描述
将某个数值在数据集中的排位作为数据集的百分比值返回,此处的百分比值的范围为 0 到 1。此函数可用于计算值在数据集内的相对位置。 例如,可以使用 PERCENTRANK 计算能力测试得分在所有测试得分中的位置。
有关新函数的详细信息,请参考PERCENTRANK.EXC 函数和PERCENTRANK.INC 函数。
用法
PERCENTRANK(array,x,[significance])
PERCENTRANK 函数用法具有下列参数:
Array必需。 定义相对位置的数值数组或数值数据区域。
X必需。 需要得到其排位的值。
significance可选。 用于标识返回的百分比值的有效位数的值。 如果省略,则 PERCENTRANK 使用 3 位小数 (0.xxx)。
备注
如果数组为空,则 PERCENTRANK 返回 错误值 #NUM!。
如果 significance < 1,则 PERCENTRANK 返回 错误值 #NUM!。
如果数组里没有与 x 相匹配的值,函数 PERCENTRANK 将进行插值以返回正确的百分比排位。
案例
POISSON 函数
描述
返回泊松分布。 泊松分布的一个常见应用是预测特定时间内的事件数,例如 1 分钟内到达收费停车场的汽车数。
有关新函数的详细信息,请参考POISSON.DIST 函数。
用法
POISSON(x,mean,cumulative)
POISSON 函数用法具有下列参数:
X必需。 事件数。
Mean必需。 期望值。
cumulative必需。 一逻辑值,确定所返回的概率分布的形式。 如果 cumulative 为 TRUE,则 POISSON 返回发生的随机事件数在零(含零)和 x(含 x)之间的累积泊松概率;如果为 FALSE,则 POISSON 返回发生的事件数正好是 x 的泊松概率密度函数。
备注
如果 x 不是整数,将被截尾取整。
如果 x 或 mean 为非数值型,则 POISSON 返回 错误值 #VALUE!。
如果 x < 0,则 POISSON 返回 错误值 #NUM!。
如果 mean < 0,则 POISSON 返回 错误值 #NUM!。
POISSON 计算如下。
对于 cumulative = FALSE:
对于 cumulative = TRUE:
案例
QUARTILE 函数
描述
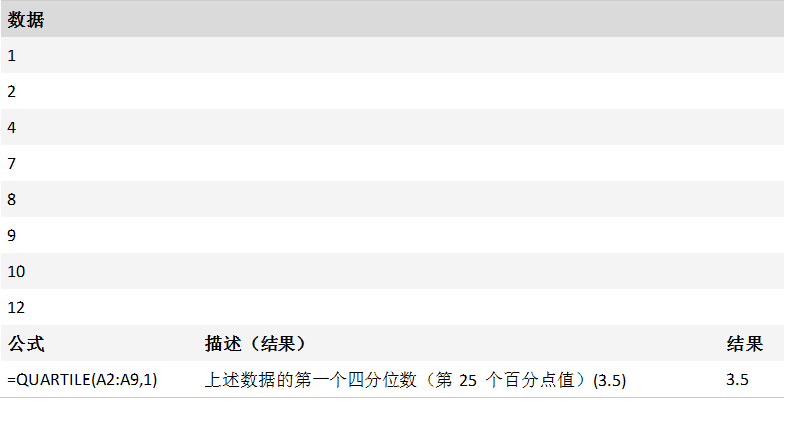
返回一组数据的四分位点。 四分位点通常用于销售和调查数据,以对总体进行分组。 例如,您可以使用 QUARTILE 查找总体中前 25% 的收入值。
有关新函数的详细信息,请参考QUARTILE.EXC 函数和QUARTILE.INC 函数。
用法
QUARTILE(array,quart)
QUARTILE 函数用法具有下列参数:
Array必需。 要求得四分位数值的数组或数字型单元格区域。
Quart必需。 指定返回哪一个值。
备注
如果 array 为空,则 QUARTILE 返回 错误值 #NUM!。
如果 quart 不为整数,将被截尾取整。
如果 quart < 0 或 quart > 4,则 QUARTILE 返回 错误值 #NUM!。
当 quart 分别等于 0、2 和 4 时,函数 MIN、MEDIAN 和 MAX 返回的值与函数 QUARTILE 返回的值相同。
案例
RANK 函数
描述
返回一列数字的数字排位。 数字的排位是其相对于列表中其他值的大小。 (如果要对列表进行排序,则数字排位可作为其位置。)
有关新函数的详细信息,请参考RANK.AVG 函数和RANK.EQ 函数。
用法
RANK(number,ref,[order])
RANK 函数用法具有下列参数:
Number必需。 要找到其排位的数字。
Ref必需。 数字列表的数组,对数字列表的引用。 Ref 中的非数字值会被忽略。
Order可选。 一个指定数字排位方式的数字。
如果 order 为 0(零)或省略,Microsoft Excel 对数字的排位是基于 ref 为按照降序排列的列表。
如果 order 不为零,Microsoft Excel 对数字的排位是基于 ref 为按照升序排列的列表。
其他
Rank 赋予重复数相同的排位。 但重复数的存在将影响后续数值的排位。 例如,在按升序排序的整数列表中,如果数字 10 出现两次,且其排位为 5,则 11 的排位为 7(没有排位为 6 的数值)。
要达到某些目的,可能需要使用将关联考虑在内的排位定义。 在上一案例中,可能需要将数字 10 的排位修改为 5.5。 这可以通过向 RANK 返回的值添加以下修正系数来实现。 此修正系数适用于按降序排序(order = 0 或省略)和按升序排序(order = 非零值)计算排位的情况。
关联排位的修正系数 =[COUNT(ref) + 1 – RANK(number, ref, 0) – RANK(number, ref, 1)]/2。
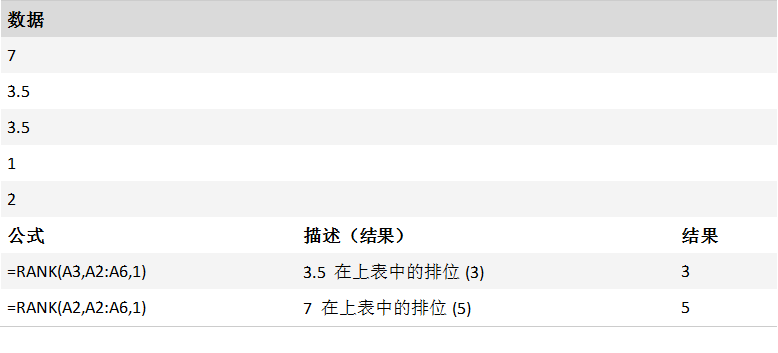
在以下案例中,RANK(A2,A1:A5,1) 等于3。 修正系数为 (5 + 1 – 2 – 3)/2 = 0.5,将关联考虑在内的修订排位为 3 + 0.5 = 3.5。 如果数字在 ref 中仅出现一次,此修正系数将为 0,因为无需调整 RANK 以进行关联。
案例
STDEV 函数
描述
根据样本估计标准偏差。标准偏差可以测量值在平均值(中值)附近分布的范围大小。
有关新函数的详细信息,请参考STDEV.S 函数。
用法
STDEV(number1,[number2],...)
STDEV 函数用法具有下列参数:
Number1必需。对应于总体样本的第一个数值参数。
Number2, ...可选。对应于总体样本的 2 到 255 个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
备注
STDEV 假定其参数是总体样本。如果数据代表整个总体,请使用 STDEVP 计算标准偏差。
此处标准偏差的计算使用“n-1”方法。
参数可以是数字或者是包含数字的名称、数组或引用。
逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用,则只计算其中的数字。数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。
如果参数为错误值或为不能转换为数字的文本,将会导致错误。
如果要使计算包含引用中的逻辑值和代表数字的文本,请使用 STDEVA 函数。
STDEV 使用下面的公式:
其中 x 为样本平均值 AVERAGE(number1,number2,…),n 为样本大小。
案例
STDEVP 函数
描述
根据作为参数给定的整个总体计算标准偏差。标准偏差可以测量值在平均值(中值)附近分布的范围大小。
有关新函数的详细信息,请参考STDEV.P 函数。
用法
STDEVP(number1,[number2],...)
STDEVP 函数用法具有下列参数:
Number1必需。对应于总体的第一个数值参数。
Number2, ...可选。对应于总体的 2 到 255 个数值参数。也可以用单一数组或对某个数组的引用来代替用逗号分隔的参数。
备注
STDEVP 假定其参数是整个总体。如果数据代表总体样本,请使用 STDEV 计算标准偏差。
对于规模很大的样本,STDEV 和 STDEVP 返回近似值。
此处标准偏差的计算使用“n”方法。
参数可以是数字或者是包含数字的名称、数组或引用。
逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用,则只计算其中的数字。数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。
如果参数为错误值或为不能转换为数字的文本,将会导致错误。
如果要使计算包含引用中的逻辑值和代表数字的文本,请使用 STDEVPA 函数。
STDEVP 使用下面的公式:
其中 x 为样本平均值 AVERAGE(number1,number2,…),n 为样本大小。
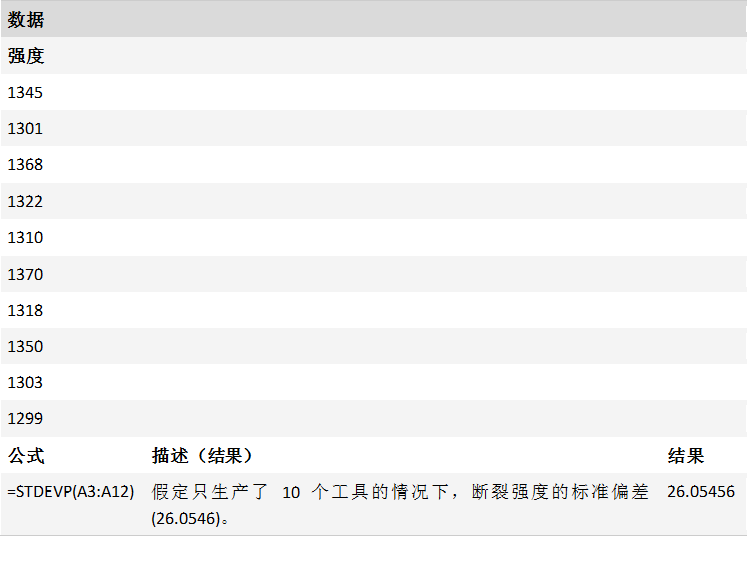
案例
TDIST 函数
描述
返回学生 t 分布的百分点(概率),其中,数字值 (x) 是用来计算百分点的 t 的计算值。 t 分布用于小型样本数据集的假设检验。 可以使用该函数代替 t 分布的临界值表。
有关新函数的详细信息,请参考T.DIST.2T 函数和T.DIST.RT 函数。
用法
TDIST(x,deg_freedom,tails)
TDIST 函数用法具有下列参数:
X必需。 需要计算分布的数值。
Deg_freedom必需。 一个表示自由度数的整数。
tails必需。 指定返回的分布函数是单尾分布还是双尾分布。 如果 Tails = 1,则 TDIST 返回单尾分布。 如果Tails = 2,则 TDIST 返回双尾分布。
备注
如果任一参数为非数值的,则 TDIST 返回错误值 #VALUE!。
如果 Deg_freedom < 1,则 TDIST 返回错误值 #NUM!。
参数 Deg_freedom 和 Tails 将被截尾取整。
如果 Tails 是除 1 或 2 之外的任何值,则 TDIST 返回 错误值 #NUM!。
如果 x < 0,则 TDIST 返回 错误值 #NUM!。
如果 Tails = 1,TDIST 的计算公式为 TDIST = P( X>x ),其中 X 为服从 t 分布的随机变量。 如果 Tails = 2,TDIST 的计算公式为 TDIST = P(|X| > x) = P(X > x or X < -x)。
因为不允许 x < 0,所以当 x < 0 时要使用 TDIST,注意 TDIST(-x,df,1) = 1 – TDIST(x,df,1) = P(X > -x) 和 TDIST(-x,df,2) = TDIST(x df,2) = P(|X| > x)。
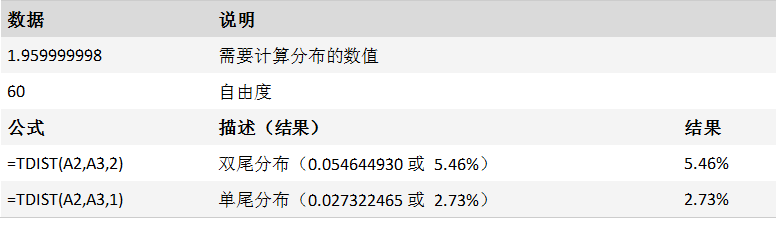
案例
TINV 函数
描述
返回学生 t 分布的双尾反函数。
有关新函数的详细信息,请参考T.INV.2T 函数或T.INV 函数。
用法
TINV(probability,deg_freedom)
TINV 函数用法具有下列参数:
Probability必需。 与双尾学生 t 分布相关的概率。
Deg_freedom必需。 代表分布的自由度数。
其他
如果任一参数是非数值的,则 TINV 返回 错误值 #VALUE!。
如果 probability <= 0 或 probability > 1,则 TINV 返回 错误值 #NUM!。
如果 deg_freedom 不是整数,则将被截尾取整。
如果 deg_freedom < 1,则 TINV 返回 错误值 #NUM!。
TINV 返回 t 值,P(|X| > t) = probability,其中 X 为服从 t 分布的随机变量,且 P(|X| > t) = P(X < -t or X > t)。
通过将 probability 替换为 2*probability,可以返回单尾 t 值。 对于概率为 0.05 以及自由度为 10 的情况,使用 TINV(0.05,10)(返回 2.28139)计算双尾值。 对于相同概率和自由度的情况,可以使用 TINV(2*0.05,10)(返回 1.812462)计算单尾值。
注意:在某些表格中,概率被描述为 (1-p)。
如果已给定概率值,则 TINV 使用 TDIST(x, deg_freedom, 2) = probability 求解数值 x。 因此,TINV 的精度取决于 TDIST 的精度。 TINV 使用迭代搜索技术。 如果搜索在 100 次迭代之后没有收敛,则函数返回错误值 #N/A。
案例
TTEST 函数
描述
返回与学生 t 检验相关的概率。 使用函数 TTEST 确定两个样本是否可能来自两个具有相同平均值的基础总体。
有关新函数的详细信息,请参考T.TEST 函数。
用法
TTEST(array1,array2,tails,type)
TTEST 函数用法具有下列参数:
Array1必需。 第一个数据集。
Array2必需。 第二个数据集。
tails必需。 指定分布尾数。 如果 tails = 1,则 TTEST 使用单尾分布。 如果 tails = 2,则 TTEST 使用双尾分布。
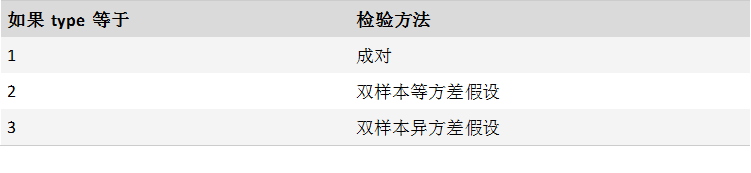
Type必需。 要执行的 t 检验的类型。
备注
如果 array1 和 array2 的数据点个数不同,且 type = 1(成对),函数 TTEST 返回错误值 #N/A。
参数 tails 和 type 将被截尾取整。
如果 tails 或 type 是非数值的,则 TTEST 返回 错误值 #VALUE!。
如果 tails 是除 1 或 2 之外的任何值,则 TTEST 返回 错误值 #NUM!。
TTEST 使用 array1 和 array2 中的数据计算非负 t 统计值。 如果 tails=1,在假设 array1 和 array2 是具有相同平均值的总体中的样本的情况下,TTEST 返回较高 t 统计值的概率。 tails=2 时,TTEST 返回的值是 tails=1 时返回值的两倍,并对应假设“总体平均值相同”时较高的 t 统计绝对值的概率。
案例
VAR 函数
描述
计算基于给定样本的方差。
有关新函数的详细信息,请参考VAR.S 函数。
用法
VAR(number1,[number2],...)
VAR 函数用法具有下列参数:
Number1必需。对应于总体样本的第一个数值参数。
Number2, ...可选。对应于总体样本的 2 到 255 个数值参数。
备注
VAR 假定其参数是总体样本。如果数据代表整个总体,请使用 VARP 计算方差。
参数可以是数字或者是包含数字的名称、数组或引用。
逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用,则只计算其中的数字。数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。
如果参数为错误值或为不能转换为数字的文本,将会导致错误。
如果要使计算包含引用中的逻辑值和代表数字的文本,请使用 VARA 函数。
VAR 使用下面的公式:
其中 x 为样本平均值 AVERAGE(number1,number2,…),n 为样本大小。
案例
VARP 函数
描述
根据整个总体计算方差。
有关新函数的详细信息,请参考VAR.P 函数。
用法
VARP(number1,[number2],...)
VARP 函数用法具有下列参数:
Number1必需。对应于总体的第一个数值参数。
Number2,...可选。对应于总体的 2 到 255 个数值参数。
备注
VARP 假定其参数是整个总体。如果数据代表总体样本,请使用 VAR 计算方差。
参数可以是数字或者是包含数字的名称、数组或引用。
逻辑值和直接键入到参数列表中代表数字的文本被计算在内。
如果参数是一个数组或引用,则只计算其中的数字。数组或引用中的空白单元格、逻辑值、文本或错误值将被忽略。
如果参数为错误值或为不能转换为数字的文本,将会导致错误。
如果要使计算包含引用中的逻辑值和代表数字的文本,请使用 VARPA 函数。
VARP 的公式为:
其中 x 为样本平均值 AVERAGE(number1,number2,…),n 为样本大小。
案例
WEIBULL 函数
描述
返回 Weibull 分布。 可以将该分布用于可靠性分析,例如计算设备出现故障的平均时间。
有关新函数的详细信息,请参考WEIBULL.DIST 函数。
用法
WEIBULL(x,alpha,beta,cumulative)
WEIBULL 函数用法具有下列参数:
X必需。 用来计算函数的值。
Alpha必需。 分布参数。
Beta必需。 分布参数。
cumulative必需。 确定函数的形式。
备注
如果 x、alpha 或 beta 是非数值的,则 WEIBULL 返回 错误值 #VALUE!。
如果 x < 0,则 WEIBULL 返回 错误值 #NUM!。
如果 alpha ≤ 0 或 beta ≤ 0,则 WEIBULL 返回 错误值 #NUM!。
Weibull 累积分布函数的公式为:
Weibull 概率密度函数的公式为:
当 alpha = 1 时,WEIBULL 使用下面的公式返回指数分布:
案例
ZTEST 函数
描述
返回 z 检验的单尾概率值。 对于给定的假设总体平均值 μ0,ZTEST 返回样本平均值大于数据集(数组)中观察平均值的概率,即观察样本平均值。
有关新函数的详细信息,请参考Z.TEST 函数。
用法
ZTEST(array,x,[sigma])
ZTEST 函数用法具有下列参数:
Array必需。 用来检验 x 的数组或数据区域。
X必需。 要测试的值。
Sigma可选。 总体(已知)标准偏差。 如果省略,则使用样本标准偏差。
备注
如果 array 为空,函数 ZTEST 返回错误值 #N/A。
不省略 sigma 时,函数 ZTEST 的计算公式如下:
省略 sigma 时,函数 ZTEST 的计算公式如下:
其中, x 为样本平均值 AVERAGE(array);s 为样本标准偏差 STDEV(array);n 为样本中的观察值个数 COUNT(array)。
ZTEST 代表基础总体平均值为 μ0 时样本平均值大于观察值 AVERAGE(array) 的概率。 在正态分布对称情况下,如果 AVERAGE(array) < μ0,则 Z.TEST 将返回的值大于 0.5。
当基础总体平均值为 μ0,样本平均值从 μ0(沿任一方向)变化到 AVERAGE(array) 时,下面的 Excel 公式可用于计算双尾概率:
=2 * MIN(ZTEST(array,μ0,sigma), 1 - ZTEST(array,μ0,sigma))。
案例
以上是所有EXCEL的兼容性函数(下)描述用法以及使用案例。这次分享中存在哪些疑问或者哪些不足,可以在下面进行评论。如果觉得不错,可以分享给你的朋友,让大家一起掌握这些excel的兼容性函数(下)。