TensorFlow2.0 学习笔记(二):多层感知机(MLP)
专栏——TensorFlow学习笔记
文章目录
- 专栏——TensorFlow学习笔记
- 一、基础知识
- 二、Keras 的模型和层
- 三、多层感知机(MLP)
- 3.1、数据获取及预处理
- 3.2、模型构建
- 3.3、模型训练
- 3.4、模型评估
- 3.5、完整代码
- 四、总结
- 推荐阅读
- 参考文章
一、基础知识
使用 TensorFlow 2.0 快速搭建动态模型,主要有四个部分:
-
模型的构建:
tf.keras.Model和tf.keras.layers -
模型的损失函数:
tf.keras.losses -
模型的优化器:
tf.keras.optimizer -
模型的评估:
tf.keras.metrics
分别通过各自的函数进行构建。
二、Keras 的模型和层
在 TensorFlow 2.0 中,推荐使用 Keras( tf.keras )构建模型。Keras 是一个广为流行的高级神经网络 API,简单、快速而不失灵活性,现已得到 TensorFlow 的官方内置和全面支持,这也是 TensorFlow 2.0 更加简洁的原因之一。
Keras 有两个重要的概念: 模型 和 层。
- 层 将各种计算流程和变量进行了封装(例如基本的全连接层,CNN 的卷积层、池化层等);
- 模型 将各种 层 进行组织和连接并封装成一个整体(例如输入数据通过各种层以及运算而得到输出等)。
Keras 在 tf.keras.layers 下内置了深度学习中大量常用的的预定义层,同时也允许进行自定义层;而在需要模型调用的时候,使用 y_pred = model(X) 的形式即可。
使用
super ()函数调用父类方法,使用__call__()方法对实例进行调用。
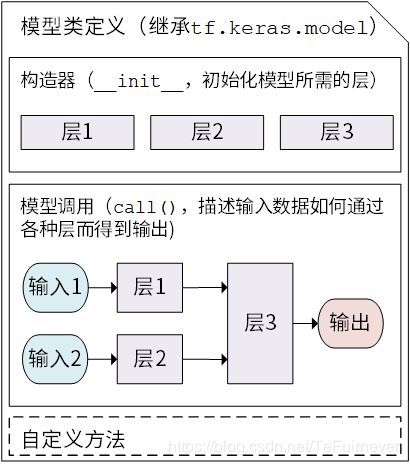
常用的模型写法是以类的形式呈现,通过继承 tf.keras.Model 这个 Python 类来定义自己的模型。在继承类中,需要重写 __init__() (构造函数,初始化)和 call(input) (模型调用)两个方法,同时也可以根据需要增加自定义的方法。
代码如下:
class Model(tf.keras.Model):
def __init__(self):
# Python 2 下使用 super(Model, self).__init__()
super().__init__()
# 此处添加初始化代码(包含 call 方法中会用到的层),例如:
layer1 = tf.keras.layers.BuiltInLayer(...)
layer2 = MyCustomLayer(...)
def call(self, input):
# 此处添加我们模型调用的代码(处理输入并返回输出),例如:
x = layer1(input)
output = layer2(x)
return output
# 还可以添加自定义的方法
继承 tf.keras.Model 后,就同时可以使用父类的若干方法和属性,例如在实例化类 model = Model() 后,可以通过 model.variables 这一属性直接获得模型中的所有变量,免去一个个显式指定变量的麻烦。
举一个例子,通过模型类的方式编写一个线性模型 y_pred = a * X + b:
import tensorflow as tf
X = tf.constant([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
y = tf.constant([[10.0], [20.0]])
class Linear(tf.keras.Model):
def __init__(self):
super().__init__()
self.dense = tf.keras.layers.Dense(
units=1,
activation=None,
kernel_initializer=tf.zeros_initializer(),
bias_initializer=tf.zeros_initializer()
)
def call(self, input):
output = self.dense(input)
return output
# 实例化类
model = Linear()
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
for i in range(100):
with tf.GradientTape() as tape:
# 调用模型 y_pred = model(X) 而不是显式写出 y_pred = a * X + b
y_pred = model(X)
# 均方误差损失函数
loss = tf.reduce_mean(tf.square(y_pred - y))
# 使用 model.variables 这一属性直接获得模型中的所有变量
grads = tape.gradient(loss, model.variables)
optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
print(model.variables)

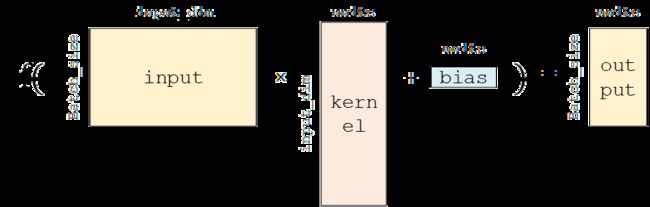
其中这个 全连接层(Fully-connected Layer) tf.keras.layers.Dense 封装了 output = activation(tf.matmul(input, kernel) + bias) 这一线性变换 + 激活函数的计算操作,kernel 和 bias 是层中可训练的变量。假设输入张量的形状为 input = [batch_size, input_dim] ,经过全连接层,输出张量的形状为 [batch_size, units] 的二维张量。
-
units:输出张量的维度; -
activation:激活函数,对应于f(AW + b)中的f,默认为无激活函数(a(x) = x)。常用的激活函数包括tf.nn.relu、tf.nn.tanh和tf.nn.sigmoid; -
use_bias:是否加入偏置向量bias,即f(AW + b)中的b。默认为True; -
kernel_initializer、bias_initializer:权重矩阵kernel和偏置向量bias两个变量的初始化器。默认为tf.glorot_uniform_initializer。设置为tf.zeros_initializer表示将两个变量均初始化为全 0;
三、多层感知机(MLP)
我们之前写过关于感知机的 numpy 代码,详细在这个博客——深度学习之手撕神经网络代码(基于numpy)。
现在基于 TensorFlow 2.0 来写一个感知机,基于一个完整的网络构建过程,主要分为四个步骤:
-
使用
tf.keras.datasets获得数据集并预处理 -
使用
tf.keras.Model和tf.keras.layers构建模型 -
训练模型,使用
tf.keras.losses计算损失函数,并使用tf.keras.optimizer优化模型 -
评估模型,使用
tf.keras.metrics计算评估指标
数据还是手写数字识别 mnist,所以解决的问题是分类问题。
3.1、数据获取及预处理
目标是使用一个简单的 MNISTLoader 类获取 MNIST 数据集数据,通过 tf.keras.datasets 进行 MNIST 数据集的快速载入。
class MNISTLoader():
def __init__(self):
mnist = tf.keras.datasets.mnist
(self.train_data, self.train_label), (self.test_data, self.test_label) = mnist.load_data()
# MNIST中的图像默认为uint8(0-255的数字)
# 以下代码将其归一化到0-1之间的浮点数,并在最后增加一维作为颜色通道
self.train_data = np.expand_dims(
self.train_data.astype(
np.float32) / 255.0,
axis=-1) # [60000, 28, 28, 1]
self.test_data = np.expand_dims(
self.test_data.astype(
np.float32) / 255.0,
axis=-1) # [10000, 28, 28, 1]
self.train_label = self.train_label.astype(np.int32) # [60000]
self.test_label = self.test_label.astype(np.int32) # [10000]
self.num_train_data, self.num_test_data = self.train_data.shape[0], self.test_data.shape[0]
def get_batch(self, batch_size):
# 从数据集中随机取出batch_size个元素并返回
index = np.random.randint(0, np.shape(self.train_data)[0], batch_size)
return self.train_data[index, :], self.train_label[index]
在 DataLoader 类中, self.train_data 和 self.test_data 分别载入了 60,000 和 10,000 张大小为 28*28 的手写体数字图片。此外,在 TensorFlow 中,图像数据集的一种典型表示是 [图像数目,长,宽,色彩通道数] 的四维张量,所以使用 np.expand_dims() 函数为图像数据手动在最后添加一维通道,又由于读入的是灰度图片,色彩通道数为 1(彩色 RGB 图像色彩通道数为 3)。
3.2、模型构建
多层感知机的模型类实现使用 tf.keras.Model 和 tf.keras.layers 构建,又多个层数(顾名思义,“多层” 感知机),以及引入了非线性激活函数(这里使用了 ReLU 函数 , 即下方的 activation=tf.nn.relu )。该模型输入一个向量(比如这里是拉直的 1×784 手写体数字图片),输出 10 维的向量,分别代表这张图片属于 0 到 9 的概率。
class MLP(tf.keras.Model):
def __init__(self):
super().__init__()
# Flatten层将除第一维(batch_size)以外的维度展平
self.flatten = tf.keras.layers.Flatten()
# 全连接层
self.dense1 = tf.keras.layers.Dense(units=100, activation=tf.nn.relu)
self.dense2 = tf.keras.layers.Dense(units=10)
def call(self, inputs): # [batch_size, 28, 28, 1]
x = self.flatten(inputs) # [batch_size, 784]
x = self.dense1(x) # [batch_size, 100]
x = self.dense2(x) # [batch_size, 10]
output = tf.nn.softmax(x)
return output
网络示意图如下:
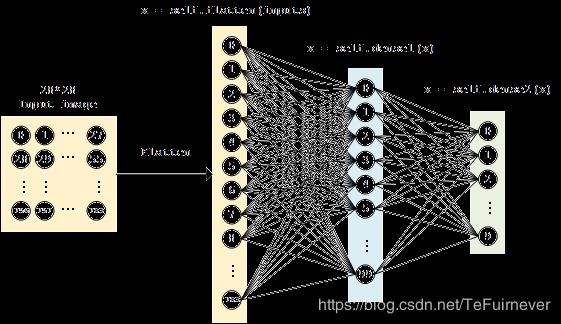
这里,因为期望的输出是 输入图片分别属于 0 到 9 的概率,也就是一个 10 维的离散概率分布,所以:
-
该向量中的每个元素均在 [0, 1] 之间;
-
该向量的所有元素之和为 1。
为了使得模型的输出能始终满足这两个条件,我们使用 Softmax 函数 (归一化指数函数, tf.nn.softmax )对模型的原始输出进行归一化,其形式为 σ ( z ) j = e z j ∑ k = 1 K e z k \sigma(\mathbf{z})_j = \frac{e^{z_j}}{\sum_{k=1}^K e^{z_k}} σ(z)j=∑k=1Kezkezj,应该说 softmax 函数是我们这里的最佳选择!!!因为它完全符合上面的两个要求。 不仅如此,softmax 函数能够 凸显原始向量中最大的值,并抑制远低于最大值的其他分量,这也是该函数被称作 softmax 函数的原因(即平滑化的 argmax 函数)。
3.3、模型训练
先定义一些模型超参数:
num_epochs = 5 # 训练轮数
batch_size = 50 # 批大小
learning_rate = 0.001 # 学习率
实例化模型和数据读取类,并实例化一个 tf.keras.optimizer 的优化器(这里使用常用的 Adam 优化器):
model = MLP() # 实例化模型
data_loader = MNISTLoader() # 数据载入
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate) # 实例化优化器
然后迭代进行以下步骤:
-
从
DataLoader中随机取一批训练数据; -
将这批数据送入模型,计算出模型的预测值
y_pred; -
将模型预测值与真实值进行比较,计算损失函数
loss; -
计算损失函数关于模型变量的导数
grads; -
将求出的导数值传入优化器
optimizer,使用优化器的apply_gradients方法更新模型参数以最小化损失函数。
具体代码实现如下:
num_batches = int(data_loader.num_train_data // batch_size * num_epochs)
for batch_index in range(num_batches):
# 随机取一批训练数据
X, y = data_loader.get_batch(batch_size)
with tf.GradientTape() as tape:
# 计算模型预测值
y_pred = model(X)
# 计算损失函数
loss = tf.keras.losses.sparse_categorical_crossentropy(
y_true=y, y_pred=y_pred)
loss = tf.reduce_mean(loss)
print("batch %d: loss %f" % (batch_index, loss.numpy()))
# 计算模型变量的导数
grads = tape.gradient(loss, model.variables)
# 优化器的使用
optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
你或许注意到了,没有显式地写出一个损失函数,而是使用 tf.keras.losses 中的 sparse_categorical_crossentropy (交叉熵)函数,将模型的预测值 y_pred 与真实的标签值 y 作为函数参数传入,由 Keras 帮助我们计算损失函数的值。
交叉熵作为损失函数,在分类问题中被广泛应用。其离散形式为
H ( y , y ^ ) = − ∑ i = 1 n y i log ( y i ^ ) H(y, \hat{y}) = -\sum_{i=1}^{n}y_i \log(\hat{y_i}) H(y,y^)=−i=1∑nyilog(yi^)
其中 y 为真实概率分布, y ^ \hat{y} y^ 为预测概率分布, n 为分类任务的类别个数。预测概率分布与真实分布越接近,则交叉熵的值越小,反之则越大,这就是交叉熵函数的优势,也是为什么分类问题中很喜欢使用交叉熵函数的原因。
注意:
loss = tf.keras.losses.sparse_categorical_crossentropy(y_true=y, y_pred=y_pred)
等价于
loss = tf.keras.losses.categorical_crossentropy(y_true=tf.one_hot(y, depth=tf.shape(y_pred)[-1]), y_pred=y_pred)
也就是说是默认使用 one-hot 编码 的,也叫 独热编码,简单来说就是把(0.3,0.6,0.1)编码成(0,1,0)。
3.4、模型评估
最后,使用测试集来评估模型的性能,即使用 tf.keras.metrics 中的 SparseCategoricalAccuracy 评估器来评估模型在测试集上的性能,该评估器能够对模型预测的结果与真实结果进行比较,并输出预测正确的样本数占总样本数的比例。
我们迭代测试数据集,每次通过 update_state() 方法向评估器输入两个参数: y_pred 和 y_true ,即模型预测出的结果和真实结果。评估器具有内部变量来保存当前评估指标相关的参数数值(例如当前已传入的累计样本数和当前预测正确的样本数)。迭代结束后,使用 result() 方法输出最终的评估指标值(预测正确的样本数占总样本数的比例)。
在以下代码中,实例化了一个 tf.keras.metrics.SparseCategoricalAccuracy 评估器,并使用 For 循环迭代分批次传入了测试集数据的预测结果与真实结果,并输出训练后的模型在测试数据集上的准确率。
# 评估器
sparse_categorical_accuracy = tf.keras.metrics.SparseCategoricalAccuracy()
# 迭代轮数
num_batches = int(data_loader.num_test_data // batch_size)
for batch_index in range(num_batches):
start_index, end_index = batch_index * batch_size, (batch_index + 1) * batch_size
# 模型预测的结果
y_pred = model.predict(data_loader.test_data[start_index: end_index])
sparse_categorical_accuracy.update_state(
y_true=data_loader.test_label[start_index: end_index], y_pred=y_pred)
print("test accuracy: %f" % sparse_categorical_accuracy.result())
3.5、完整代码
完整的代码如下:
import tensorflow as tf
import numpy as np
class MNISTLoader():
def __init__(self):
mnist = tf.keras.datasets.mnist
(self.train_data, self.train_label), (self.test_data,
self.test_label) = mnist.load_data()
# MNIST中的图像默认为uint8(0-255的数字)
# 以下代码将其归一化到0-1之间的浮点数,并在最后增加一维作为颜色通道
self.train_data = np.expand_dims(
self.train_data.astype(
np.float32) / 255.0,
axis=-1) # [60000, 28, 28, 1]
self.test_data = np.expand_dims(
self.test_data.astype(
np.float32) / 255.0,
axis=-1) # [10000, 28, 28, 1]
self.train_label = self.train_label.astype(np.int32) # [60000]
self.test_label = self.test_label.astype(np.int32) # [10000]
self.num_train_data, self.num_test_data = self.train_data.shape[
0], self.test_data.shape[0]
def get_batch(self, batch_size):
# 从数据集中随机取出batch_size个元素并返回
index = np.random.randint(0, np.shape(self.train_data)[0], batch_size)
return self.train_data[index, :], self.train_label[index]
class MLP(tf.keras.Model):
def __init__(self):
super().__init__()
# Flatten层将除第一维(batch_size)以外的维度展平
self.flatten = tf.keras.layers.Flatten()
# 全连接层
self.dense1 = tf.keras.layers.Dense(units=100, activation=tf.nn.relu)
self.dense2 = tf.keras.layers.Dense(units=10)
def call(self, inputs): # [batch_size, 28, 28, 1]
x = self.flatten(inputs) # [batch_size, 784]
x = self.dense1(x) # [batch_size, 100]
x = self.dense2(x) # [batch_size, 10]
output = tf.nn.softmax(x)
return output
num_epochs = 5 # 训练轮数
batch_size = 50 # 批大小
learning_rate = 0.001 # 学习率
model = MLP() # 实例化模型
data_loader = MNISTLoader() # 数据载入
optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate) # 实例化优化器
num_batches = int(data_loader.num_train_data // batch_size * num_epochs)
for batch_index in range(num_batches):
# 随机取一批训练数据
X, y = data_loader.get_batch(batch_size)
with tf.GradientTape() as tape:
# 计算模型预测值
y_pred = model(X)
# 计算损失函数
loss = tf.keras.losses.sparse_categorical_crossentropy(
y_true=y, y_pred=y_pred)
loss = tf.reduce_mean(loss)
print("batch %d: loss %f" % (batch_index, loss.numpy()))
# 计算模型变量的导数
grads = tape.gradient(loss, model.variables)
# 优化器的使用
optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))
# 评估器
sparse_categorical_accuracy = tf.keras.metrics.SparseCategoricalAccuracy()
# 迭代轮数
num_batches = int(data_loader.num_test_data // batch_size)
for batch_index in range(num_batches):
start_index, end_index = batch_index * \
batch_size, (batch_index + 1) * batch_size
# 模型预测的结果
y_pred = model.predict(data_loader.test_data[start_index: end_index])
sparse_categorical_accuracy.update_state(
y_true=data_loader.test_label[start_index: end_index], y_pred=y_pred)
print("test accuracy: %f" % sparse_categorical_accuracy.result())
输出结果:
# 测试了五次
test accuracy: 0.974600
test accuracy: 0.973600
test accuracy: 0.975200
test accuracy: 0.972600
test accuracy: 0.975200
第一次结果图如下:
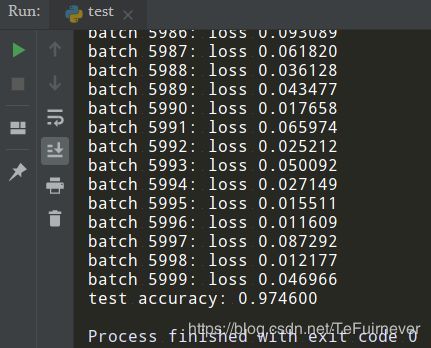
可以注意到,使用这样简单的一个模型(多层感知机),就已经可以达到 97% 左右的准确率。
四、总结
还是和 深度学习之手撕神经网络代码(基于numpy) 进行对比,可以看得出整个令人厌烦的数学过程变得简单的多,数学帕金森患者不必忧虑了,通过慢慢地复现不同的网络,也能感知到 2.0 和 1.x 的区别是让人动容的,我反正是哭了,期待接下来的 CNN 复现了!
推荐阅读
- TensorFlow2.0 学习笔记(一):TensorFlow 2.0 的安装和环境配置以及上手初体验
- TensorFlow2.0 学习笔记(二):多层感知机(MLP)
- TensorFlow2.0 学习笔记(三):卷积神经网络(CNN)
- TensorFlow2.0 学习笔记(四):迁移学习(MobileNetV2)
- TensorFlow2.0 学习笔记(五):循环神经网络(RNN)
参考文章
- TensorFlow 官方文档
- 简单粗暴 TensorFlow 2.0