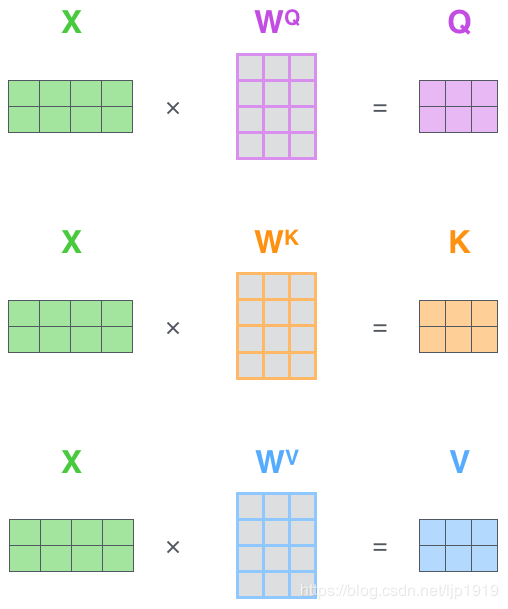Transformer学习笔记

0-背景

机构：Google 大脑
作者：Ashish Vaswani等
发表会议：NIPS2017
面向任务：机器翻译
论文地址：https://arxiv.org/abs/1706.03762
论文代码：https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/models/transformer.py

本文主要介绍Transformer(注：近期出现了Transformer-XL)的原理及其具体应用。

动机：机器翻译任务使用Encoder—Decoder模型过程中抛弃RNN或者CNN模型，只使用attention机制。采用Attention机制的原因是考虑到RNN（或者LSTM，GRU等）的计算限制为是顺序的，也就是说RNN相关算法只能从左向右依次计算或者从右向左依次计算，这种机制带来了两个问题：

• 时间片 t 的计算依赖 t-1 时刻的计算结果，这样限制了模型的并行能力；
• 顺序计算的过程中信息会丢失，尽管LSTM等门机制的结构一定程度上缓解了长期依赖的问题，但是对于特别长期的依赖现象,LSTM依旧无能为力。而如果采用CNN，虽然具备良好的并行条件，但是通过加深层深的方式获得更大的感受野，捕获长距离特征方向仍然很受限。或许后期CNN还有其他方式可以解决这个问题。

Transformer的提出解决了上面两个问题，首先它使用了Attention机制，将序列中的任意两个位置之间的距离是缩小为一个常量；其次它不是类似RNN的顺序结构，因此具有更好的并行性，符合现有的GPU框架。

效果：

WMT 2014 英-德数据集中获得28.4 BLEU(state-of-the-art)
WMT 2014 英-法数据集中获得41.8 BLEU(state-of-the-art)

另外，Transformer模型具有良好的泛化能力。后续还继续发展了Universal Transformers通用Transformer和BERT。BERT是第一个深度双向、无监督的语言表示，仅使用纯文本语料库进行预训练，然后可以使用迁移学习对各种自然语言任务进行微调的框架。

1-模型介绍

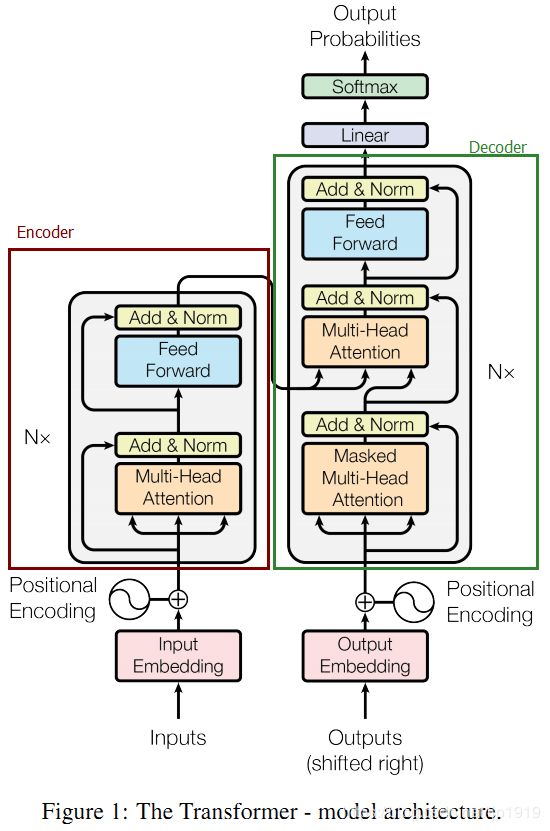
Transformer的结构由Encoder和Decoder组成：

1-1 Encoder和Decoder：

Encoder结构

Encoder由N=6个相同的layer（也称一个layer为Block）组成，layer指的就是上图左侧的单元，最左边有个“Nx”，这里是$6$个。每个Layer由两个sub-layer组成：

• muti-head self-attention (自注意力机制)
• fully connected feed forward (全连接层)

其中每个sub-layer都加了residual connection（残差连接）和normalisation，因此可以将sub-layer的输出表示为：$LayerNorm(x+Sublayer(x))$

具体每个sub-layer的含义在后续章节进行详解，这里仅仅是绘制轮廓的方式展示整个框架。

Decoder结构

Decoder和Encoder的结构差不多，但是多了一个Multi-head self-attention的sub-layer。Decoder也是由6个Transformer Block组成。每个Block组成：

• masked multi-head self-attention：发生在 Decoder 层内，上一个 Decoder 的output 作为当前Decoder 的input（即为了预测当前i位置的输出，利用了i-1位置Decoder的输出作为输入的一部分）。另外为确保位置i的输出仅依靠位置小于i的input（即确保预测第i个位置时不会接触到未来的信息），所以加入了一个mask。
• muti-head attention：Encoder 层的output作为该子层的input。所以，这一sub-layer的attention不是self-attention。
• fully connected feed forward (全连接层)

我们再从Decoder的输入、输出简述下Decode过程：
输入： Encoder的输出、i-1（上一个字符）位置Decoder的输出
输出： $i$位置输出词的概率分布
解码： Encoder可以并行计算，一次性全部encoding出来，但Decoder不是一次把所有序列解出来的，而是如RNN一个一个解出来的，因为要用上一个位置的输入当作attention的query。

过程介绍

Encoder：
Encoder通过处理输入序列开启工作。顶端Encoder的输出之后会变转化为一个包含向量K（键向量）和V（值向量）的注意力向量集。这些向量将被每个Decoder用于自身的“Encoder-Decoder注意力层”，而这些层可以帮助Decoder关注输入序列哪些位置合适：

Decoder：
Decoder阶段的每个步骤都会输出一个输出序列（在这个例子里，是翻译出的句子）的元素。接下来的步骤重复了这个过程，直到到达一个特殊的终止符号，它表示transformer的解码器已经完成了它的输出。每个步骤的输出在下一个时间步被提供给底端Decoder，这些Decoder会输出它们的解码结果。另外，与Encoder的输入类似，对Decoder的输入进行嵌入并添加位置编码。

另外Decoder中的自注意力层表现的模式与Encoder不同：在Decoder中，自注意力层只被允许处理输出序列中更靠前的那些位置。在softmax步骤前，它会把后面的位置给隐去（通过mask将它们设为-inf）。

Decoder中的“Encoder-Decoder注意力层”工作方式基本就像muti-head attention一样，只不过它是通过在它下面的层来创造query matrix（查询矩阵）， 并且从Encoder的输出中取得key/value matrix。
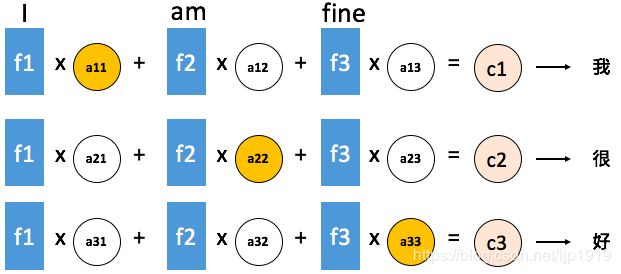
从Encoder 层到Decoder 层的途中，因为有文字序列的问题需要进行编码，例如输入序列是「I am fine」，以英文翻译成中文为例：

线性变换和Softmax层：
Decoder组件最后会输出一个实数向量。通过线性变换层把浮点数变成一个单词。线性变换层是一个简单的全连接神经网络，它可以把Decoder组件产生的向量投射到一个比它大得多的、被称作对数几率（logits）的向量里。不妨假设模型从训练集中学习一万个不同的英语单词（模型的“输出词表”）。因此对数几率向量为一万个单元格长度的向量——每个单元格对应某一个单词的分数。接下来的Softmax 层便会把那些分数变成概率（都为正数、上限1.0）。概率最高的单元格被选中， 并且它对应的单词被作为这个时间步的输出。

这张图片从底部以Decoder组件产生的输出向量开始。之后它会转化出一个输出单词。

1-2 Attention介绍

Attention机制其实就是一系列权重参数用以区别对待句子中的不同word。没有Attention的Encoder-Decoder如下：

比如，‘I like deep learning’被编码(语义编码)成C，然后在经过非线性函数$g$来Decoder得到目标Target中的每一个单词$y1$,$y2$,$y3$。计算如下：

$$\begin{gathered} C=f(x1,x2,x3) \\ y1=g(C) \\ y2=g(C,y1) \\ y3=g(C,y1,y2) \end{gathered}$$

可以看出编码结果对输出的贡献是相同的，可实际上，"I"这个word对target中的"我"的结果是影响最大的，其他word的影响几乎可以忽略。但是在上述模型中，这个重要程度没有被体现出来。Attention机制就是要从序列中学习到每一个word的重要程度。这就表明了序列元素在Encoder的时候，所对应的语义编码C是不一样的。所以$C$就不单单是$x1,x2,x3$简单的Encoder，而是成为了各个元素按其重要度加权求和得到的。也即:

$$C_i=\sum _{j=0}^{L_x}{a}_{ij}f(x_j)$$

其中$i$表示时刻，$j$表示序列中第$j$个元素，$L_x$表示序列的长度，$f()$表示word（如果不特指NLP领域的话，用元素来作为指代）$x_j$的编码。

以下以seq2seq + attention为例详细说明Attention机制在Encoder-Decoder中是如何引入的。

Attention流程：

1-隐状态准备阶段
假设已有第一个decoder的隐状态 (图中红色部分)和全部encoder的隐状态(图中绿色部分)。下图示例中有1个当前decoder的隐状态和4个encoder的隐状态。

2-对每个encoder的隐状态计算一个score

这里我们的score function采用dot product，即直接计算decoder隐状态和encoder隐状态的点乘。当然也可以选择其他的score functions。

decoder_hidden = [10, 5, 10]
encoder_hidden  score
---------------------
     [0, 1, 1]     15 (= 10×0 + 5×1 + 10×1, the dot product)
     [5, 0, 1]     60
     [1, 1, 0]     15
     [0, 5, 1]     35

3-将所有的score输入到softmax

此时其实是将score进行归一化，结果记为score^。其结果是将注意力集中到[5, 0, 1]身上。

encoder_hidden  score  score^
-----------------------------
     [0, 1, 1]     15       0
     [5, 0, 1]     60       1
     [1, 1, 0]     15       0
     [0, 5, 1]     35       0

4-将softmax结果与每个Encoder的隐状态相乘

softmax与Encoder的隐状态乘积结果为alignment vector（也称为annotation vector）。

encoder_hidden  score  score^  alignment
----------------------------------------
     [0, 1, 1]     15       0  [0, 0, 0]
     [5, 0, 1]     60       1  [5, 0, 1]
     [1, 1, 0]     15       0  [0, 0, 0]
     [0, 5, 1]     35       0  [0, 0, 0]

从aligment vector可以看出抑制无关元素，抽取相关元素。一般情况下的softmax结果是浮点数，不会如这里例子中一个1，其余都是0这种完美情况。

5-将alignment vectors进行求和
将alignment vectors进行求和得到context vector：

context vector是alignment vectors的信息集成。

encoder_hidden  score  score^  alignment
----------------------------------------
     [0, 1, 1]     15       0  [0, 0, 0]
     [5, 0, 1]     60       1  [5, 0, 1]
     [1, 1, 0]     15       0  [0, 0, 0]
     [0, 5, 1]     35       0  [0, 0, 0]
context = [0+5+0+0, 0+0+0+0, 0+1+0+0] = [5, 0, 1]

6-将context vector输入到decoder
这部分取决于具体的框架设计：

Attention整个流程：

PS：主要参考资料3

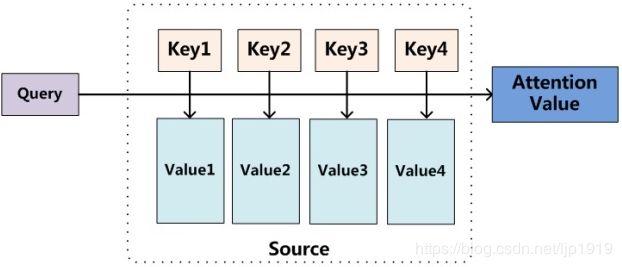
Attention函数：

为了获得Attention的一组注意力分配系数，引入Attention函数，它是用来得到attention value的。 Attention函数的本质可以被描述为一个查询（query）与一系列（键key-值value）对一起映射成一个output（输出）。其中query, keys, values和output都是vector。output是value的加权求和，而每个value权重是将query及其对应的key输入到compatibility function所得到的结果。

Attention value的获得分为以下3步：

• 相似度计算：将query和每个key进行相似度计算得到权重。常用的相似度函数有点积，拼接，感知机等
• 归一化：使用一个softmax(因为是一系列的k/v，所以类似多分类，要用softmax)函数对这些权重进行归一化
• 将归一化的权重和相应的键值value进行加权求和得到最后的Attention Value，即为注意力值。

$$attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

机器翻译里的源语言的Encoder输出$h_j$就是$V$
机器翻译里的源语言的Encoder输出$h_j$同样是$K$
机器翻译里的目标语言的隐层状态$z_i$就是$Q$
机器翻译里的目标语言和源语言的匹配程度$e_{ij}$就是$\frac{Q{K}^T}{\sqrt{d_k}}$
机器翻译里的归一化后的目标语言和源语言的匹配程度$a_{ij}$就是$softmax(\frac{Q{K}^T}{\sqrt{d_k}})$
机器翻译里的$c_i$就是最终的$attention(Q,K,V)$
所以说，机器翻译的attention，本质就是想给源语言Encoder输出的每一个元素$h_j$ (即V) 搞一个权重，然后加权求和。而这个权重是通$h_j$ 它自己 (即K=V) 与目标语言的隐层状态$z_i$ (即Q) 进行变换得到的。
即k=v=源语言的encoder输出，q=目标语言的隐层状态。

Self-Attention即K=V=Q。例如输入一个句子，那么里面的每个词都要和该句子中的所有词进行Attention计算。目的是学习句子内部的词依赖关系，捕获句子的内部结构。Self-Attention也正是Transformer中使用的Attention。

Self-Attention

下面介绍Self-Attention的计算实例以进一步说明。假设输入句子是"Thinking Machines"。Self-Attention的计算：

第一步：
从每个Encoder的输入向量（每个单词的词向量）中生成三个向量。也就是说对于每个单词，创造一个查询向量（Query vector）、一个键向量（Key vector）和一个值向量（Value vector）。这三个向量是通过词嵌入与三个权重矩阵后相乘创建的。这三个权重矩阵也是在训练过程中学习到的参数。

可以发现这些新向量在维度上比词嵌入向量更低。他们的维度是64，而词嵌入和编码器的输入/输出向量的维度是512. 但实际上不强求维度更小，这只是一种基于架构上的选择，它可以使multi-headed attention的大部分计算保持不变。

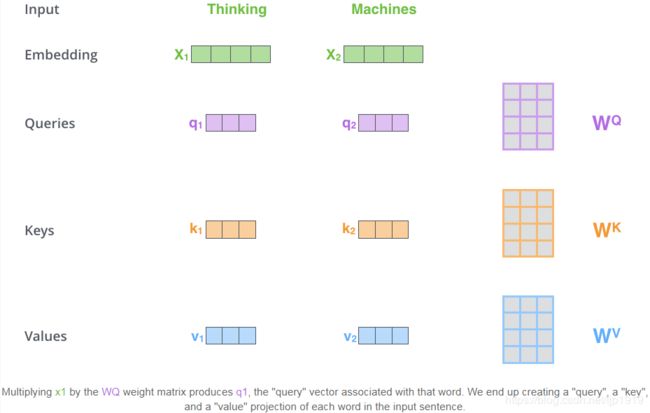
$X_1$与$W^Q$权重矩阵相乘得到$q_1$，就是与这个单词相关的查询向量。最终使得输入序列的每个单词的创建一个查询向量、一个键向量和一个值向量

第二步：
计算得分。假设为这个例子中的第一个词“Thinking”计算自注意力向量，需要拿输入句子中的每个单词对“Thinking”打分。这些分数决定了在Encode单词“Thinking”的过程中有多重视句子的其它部分。这些分数是通过打分单词（所有输入句子的单词）的Key Vector（键向量）与“Thinking”的Query vector（查询向量）的dot product（点积）来计算的。所以如果处理位置最靠前的词，即第1个单词的自注意力的话，第一个分数是$q_1和k_1$的点积，第二个分数是$q_1和k_2$的点积。

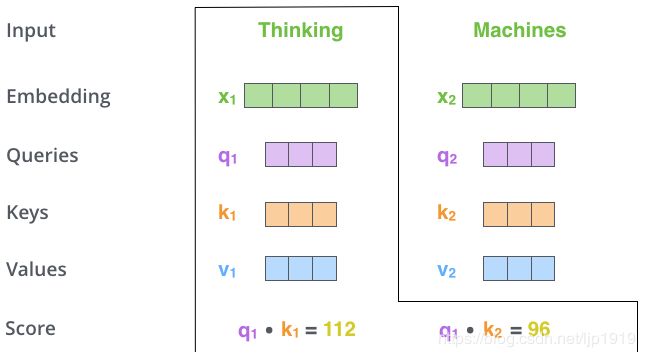
第三步和第四步：
将分数除以8(8是论文中使用的Key Vector的维数64的平方根，这会让梯度更稳定。这里也可以使用其它值，8只是默认值)，然后输入到softmax。softmax的作用是使所有单词的分数归一化，得到的分数都是正值且和为1。注意，self-attention一般是没有除以这个根号$d_k$，这里是论文作者修正的版本。

这个softmax分数决定了每个单词对Encode当下位置（“Thinking”）的贡献。显然，已经在这个位置上的单词将获得最高的softmax分数，但有时关注另一个与当前单词相关的单词也会有帮助。

第五步：
将每个Value Vector乘以softmax分数(这是为了准备之后将它们求和)。这里的直觉是希望关注语义上相关的单词，并弱化不相关的单词(例如，让它们乘以0.001这样的小数)。

第六步：
对加权的value vectors求和（注：自注意力的另一种解释就是在Encode某个单词时，就是将所有单词的表示（value vector）进行加权求和，而权重是通过该词的表示（key vector）与被编码词表示（query vector）的点积并通过softmax得到）。然后即得到自注意力层在该位置的输出(本文例子中是对于第一个单词)。

如此自注意力的计算就完成了。得到的向量就可以传给前馈神经网络。然而实际中，这些计算是以矩阵形式完成的，以便算得更快。那接下来就看看如何用矩阵实现的。

通过矩阵运算实现自注意力机制

第一步：
计算 Query matrice, Key matrice和Value matrice。为此，将输入句子的词嵌入装进矩阵$X$中， 将其乘以训练的权重矩阵$(W^Q，W^K，W^V)$

$X$矩阵中的每一行对应于输入句子中的一个单词。我们再次看到词嵌入向量 (512，或图中的4个格子)和q/k/v向量(64，或图中的3个格子)的大小差异。
最后，由于处理的是矩阵，我们可以将步骤2到步骤6合并为一个公式来计算自注意力层的输出。自注意力的矩阵运算形式：

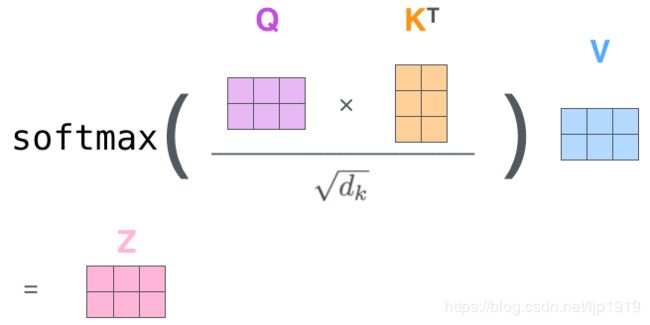
目前在NLP研究中，key和value常常都是同一个，即 key=value。这时计算出的attention value是一个向量， 代表序列元素$x_j$的编码向量。 此向量中包含了元素$x_j$的上下文关系，即包含全局联系也拥有局部联系。全局联系是因为在求相似度的时候，序列中元素与其他所有元素的相似度计算，然后加权得到了编码向量。局部联系，因为它所计算出的attention value是属于当前输入的$x_j$的。这也就是attention的强大优势之一，它可以灵活的捕捉长程和局部依赖，而且是一步到位的。

Multi-head self-attention

按照论文中的做法其实是对于多个Scaled Dot-Product Attention进行堆叠分开处理，再拼接就形成了Multi-head self-attention。论文中原图如下：

Scaled Dot-Product Attention和Multi-Head Attention

Scaled Dot-Product Attention实际上就是上文介绍self-attention。前文也介绍过了，与其他self-attention不同之处就是除以$\sqrt{d_k}$。这个尺度变换操作是为了防止dot products量纲过大，导致softmax的梯度极小，进而导致训练不稳定。这个$\sqrt{d_k}$就是所谓的scaled，本质上还是dot product。

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

multi-head attention则是通过h个不同的线性变换对Q，K，V进行投影，最后将不同的attention结果拼接起来：
$$\begin{gathered} MultiHead(Q,K,V)=Concat(hea{d}_1,...,hea{d}_h)W^o \\ 其中hea{d}_i=Attention(Q{W}_i^Q,K{W}_i^K,V{W}_i^V) \end{gathered}$$

这种通过增加“multi-headed” attention（“多头”注意力）的机制，进一步完善了自注意力层，并在两方面提高了注意力层的性能：

• 它扩展了模型专注于不同位置的能力。在上面的例子中，虽然每个编码都在$z_1$中有或多或少的体现，但是它可能被实际的单词本身所支配。如果翻译一个句子，比如“The animal didn’t cross the street because it was too tired”，我们会想知道“it”指的是哪个词，这时模型的“多头”注意机制会起到作用。
• 它给出了注意力层的多个“表示子空间”（representation subspaces）。 对于“多头”注意机制，我们有多个查询/键/值权重矩阵集(Transformer使用8个注意力头，因此对于每个Encoder/Decoder有8个矩阵集合)。这些集合中的每一个都是随机初始化的，在训练之后，每个集合都被用来将输入词嵌入(或来自较低编码器/解码器的向量)投影到不同的表示子空间中。
  

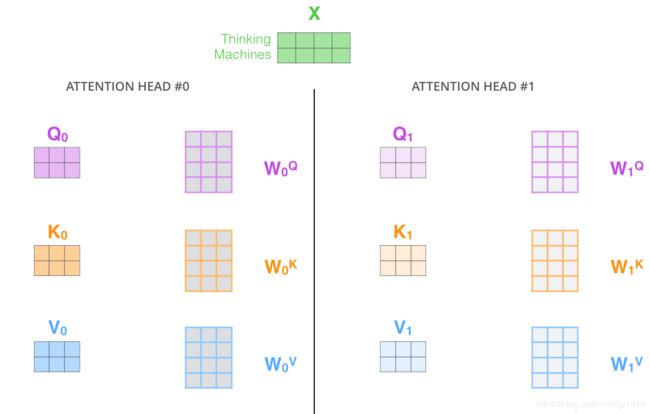
在“多头”注意机制下，为每个head保持独立的query/key/value权重矩阵，从而产生不同的query/key/value矩阵。和之前一样，拿$X$乘以$W^Q/W^K/W^V$矩阵来产生查query/key/value 矩阵。
如果按照此前介绍的自注意力计算方式，运行8次，根据8个不同的权重矩阵运算，就会得到8个不同的$Z$矩阵。

但是问题来了，前馈层不需要8个矩阵，它只需要一个矩阵(由每一个单词的表示向量组成)。所以我们需要一种方法把这8个矩阵压缩成一个矩阵。那该怎么做？其实可以直接把这些矩阵拼接在一起，然后用一个附加的权重矩阵$W^O$与它们相乘。

这几乎就是Multi-head self-attention（多头自注意力）的全部。这确实有好多矩阵，把它们集中在一个图片中，这样可以一眼看清。

小结

整个框架有3处的Attention。

1、Encoder自身的self-attention，Q K V均来自于前面一层输出，当前层的每个position可以attend到前面一层的所有位置。
2、Deocder自身的self-attention，同理，不同之处在于为了避免信息向左流动，在decoder内的scaled dot-attention加了一个mask-out层（Encoder没有），将所有在softmax的全连接层的非法连接屏蔽掉（置为-∞）
3、Encoder-Decoder attention，Query来自上一位置Decoder的输出，K、V均来自于Encoder的输出。这一步操作模拟了传统机器翻译中的attention过程（信息的交互）。

1-3 Position-wise feed-forward networks

第二个sub-layer是个全连接层。在Encoder和Decoder中都有一个全连接层。这个全连接有两层，第一层的激活函数是$ReLU$，relu的数学表达式就是f(x)=max(0,x)，第二层是一个线性激活函数（Wx+b），可以表示为：

之所以是position-wise（输入和输出的维度是一样的）是因为处理的attention输出是某一个位置$i$的attention输出。hidden_size变化为：768->3072->768（或者512->2048->512）。

1-4 Positional Encoding

Transformer抛弃了RNN，而RNN最大的一大优点是在时间序列上的先后顺序信息。Transformer综合attention 模型在做的事情，顶多是一个非常精妙的『词袋模型』而已。为了利用序列的位置信息，在模型中引入位置编码以记录序列中token之间的相对或者绝对位置信息。Transformer 为每个输入的词嵌入添加了一个向量。这些向量遵循模型学习到的特定模式，这有助于确定每个单词的位置，或序列中不同单词之间的距离。这里的直觉是，将位置向量添加到词嵌入中使得它们在接下来的运算中，能够更好地表达的词与词之间的距离。

为了让模型理解单词的顺序而添加的位置编码向量遵循特定的模式。

如果我们假设词嵌入的维数为4，则实际的位置编码如下：

尺寸为4的词嵌入位置编码实例，positional encoding的维度与embedding维度是相同的，才能够相加。

文章提到了两种Positional Encoding的方法：

• 用不同频率的sine和cosine函数直接计算（公式法）
• 学习出一份positional embedding（常规法）

经过实验发现两者的结果一样，所以最后选择了第一种方法，公式如下：

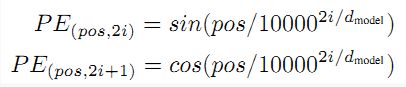
其中$pos$是位置，$i$是维度（第i个维度），这意味着positional encoding的每一个维度都对应了一个正弦曲线，波长区间为$2\pi 10000\times 2\pi$，作者认为这种方法可以使模型更容易去学得attend相对位置。比如固定一个偏移量$k$，$P{E}_{pos+k}$的结果可以用$P{E}_{pos}$通过一个线性函数来获得。
根据公式
$$sin(\alpha +\beta )=sin\alpha cos\beta +cos\alpha sin\beta$$
以及
$$cos(\alpha +\beta )=cos\alpha cos\beta -sin\alpha sin\beta$$

表明位置$k+p$的位置向量可以表示为位置$k$的特征向量的线性变化，这为模型捕捉单词之间的相对位置关系提供了非常大的便利。

1-5 Residuals

此外，Encoder和Decoder中都存在残差连接：在每个Encoder（或者Decoder）中的每个子层（自注意力、前馈网络）的周围都有一个残差连接，随后再紧跟一个"layer-normalization"步骤。

如果可视化这些向量以及这个和自注意力相关联的layer-normalization操作，那么看起来就像下面这张图描述一样：

解码器的子层也是这样样的。如果我们想象一个2 层编码-解码结构的transformer，它看起来会像下面这张图一样：

1-6 训练部分总结

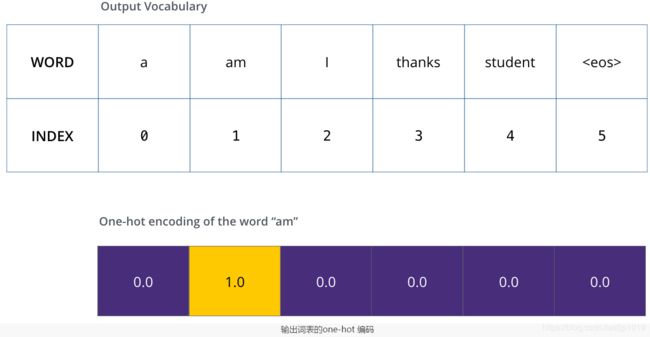
在训练过程中，训练集通过未经训练的模型进行前向传播，再用它的输出去与真实的输出做比较。为了把这个流程可视化，不妨假设输出词汇仅仅包含六个单词：“a”, “am”, “i”, “thanks”, “student”以及 “”（end of sentence的缩写形式）。

模型的输出词表在训练之前的预处理流程中就被设定好。一旦定义了输出词表，我们可以使用一个相同宽度的向量来表示词汇表中的每一个单词。这也被认为是一个one-hot 编码。所以，可以用下面这个向量来表示单词“am”：

2-模型效果

跟过去RNN、CNN相比，在效率上可以并行化训练，减少训练时间，在训练成本最小的情况下达到了最佳性能。
英-德机器翻译BLEU值28.4 (当时最好)
英-法机器翻译BLEU值41.0 (当时最好，后来被微软的**推敲网络（Deliberation Networks）**超越达到41.5)

3-模型评价

优点：
(1)相对于CNN有卷积核size限制，提取dependency的范围有限，本文的attention机制则抓取了全局的内部关联信息，获取到long-range dependencies。
(2)相比于CNN、RNN，降低了计算复杂度，并且训练可以实现并行，速度快。
(3)不会出现RNN内部可能存在的信息重叠的问题、没有过多的信息堆积、冗余、丢失

缺点：
(1)实践上：有些rnn轻易可以解决的问题transformer没做到，比如复制string或则简单的逻辑推理，尤其是碰到比训练时的sequence更长的时。
(2)理论上：Transformers非computationally universal（图灵完备），这限制了其理论表达能力，比如无法实现“while”循环
(3)粗暴的抛弃RNN和CNN也使模型丧失了捕捉局部特征的能力，RNN + CNN + Transformer的结合可能会带来更好的效果。
(4)Transformer 失去的位置信息其实在NLP中非常重要，而论文中在特征向量中加入Position Embedding也只是一个权宜之计，并没有改变Transformer结构上的固有缺陷。

4-参考资料：

1. https://arxiv.org/abs/1706.03762
2. http://jalammar.github.io/illustrated-transformer/
3. https://towardsdatascience.com/attn-illustrated-attention-5ec4ad276ee3
4. https://daiwk.github.io/posts/nlp-self-attention-models.html
5. https://github.com/tensorflow/models/tree/master/official/transformer
6. https://medium.com/@cyeninesky3/attention-is-all-you-need-基於注意力機制的機器翻譯模型-dcc12d251449