RNN循环神经网络的原理与TensorFlow实现

本文部分内容引用了以下文章及书籍，在此由衷感谢以下作者的分享！

1. https://blog.csdn.net/zhaojc1995/article/details/80572098
2. https://github.com/exacity/deeplearningbook-chinese/releases
3. 《TensorFlow实战Google深度学习框架》
4. https://blog.csdn.net/clayanddev/article/details/53947012?utm_source=blogkpcl2#正文
5. 《面向机器智能的TensorFlow实践》
6. https://github.com/exacity/deeplearningbook-chinese/releases

1.循环神经网络简介

传统的机器学习算法非常依赖于人工特征的提取，而基于全连接神经网络的方法也存在参数太多，无法利用数据中时间序列信息等问题。
循环神经网络的主要用途是处理和预测序列数据。从网络结构上，循环神经网络会记忆之前的信息，并利用之前的信息影响后面结点的输出。也就是说，循环神经网络的隐藏层之间的结点是有连接的，隐藏层的输入不仅包括输入层的输出，还包括上一时刻隐藏层的输出。
正如卷积网络可以很容易地扩展到具有很大宽度和高度的图像，以及处理大小可变的图像，循环网络可以扩展到更长的序列（比不基于序列的特化网络长得多）。大多数循环网络也能处理可变长度的序列。

2.循环神经网络结构

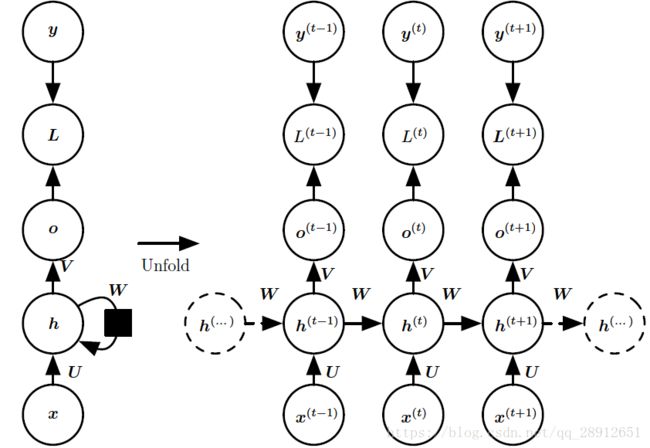
Fig.1. 计算循环网络(将x 值的输入序列映射到输出值o 的对应序列) 训练损失的计算图。损失L衡量每个o与相应的训练目标y的距离。当使用$softmax$输出时，我们假设o是未归一化的对数概率。损失L内部计算$\hat{y}=softmax(o)$，并将其与目标y比较。RNN输入到隐藏的连接由权重矩阵U参数化，隐藏到隐藏的循环连接由权重矩阵W参数化以及隐藏到输出的连接由权重矩阵V参数化。(左) 使用循环连接绘制的RNN和它的损失。(右) 同一网络被视为展开的计算图，其中每个节点现在与一个特定的时间实例相关联。

2.1循环神经网络中一些重要的设计模式包括以下几种：

1. 每个时间步都有输出，并且隐藏单元之间有循环连接的循环网络，如Fig.1 所示。
2. 每个时间步都产生一个输出，只有当前时刻的输出到下个时刻的隐藏单元之间有循环连接的循环网络。
3. 隐藏单元之间存在循环连接，但读取整个序列后产生单个输出的循环网络。

现在我们研究Fig.1中RNN 的前向传播公式。这个图没有指定隐藏单元的激活函数。我们假设使用双曲正切激活函数。此外，图中没有明确指定何种形式的输出和损失函数。我们假定输出是离散的，如用于预测词或字符的RNN。表示离散变量的常规方式是把输出o 作为每个离散变量可能值的非标准化对数概率。然后，我们可以应用softmax 函数后续处理后，获得标准化后概率的输出向量$\hat{y}$。RNN 从特定的初始状态h(0) 开始前向传播。从t = 1 到t = τ 的每个时间步，我们应用以下更新方程：
$$\begin{gathered} a^{(t)}=b+W{h}^{(t-1)}+U{x}^{(t)},(1) \\ {h}^{(t)}=tanh(a^{(t)}),(2) \\ {o}^{(t)}=c+V{h}^{(t)},(3) \\ {\hat{y}}^{(t)}=softmax(o^{(t)}),(4) \end{gathered}$$其中的参数的偏置向量b和c连同权重矩阵U、V和W,分别对应于输入到隐藏、隐藏到输出和隐藏到隐藏的连接。这个循环网络将一个输入序列映射到相同长度的输出序列。与x序列配对的y的总损失就是所有时间步的损失之和。例如，$L^{(t)}$为给定的$x^{(1)},...,x^{(t)}$后$y^{(t)}$的负对数似然，则
$$\begin{gathered} L(x^{(1)},...,x^{(\tau )},y^{(1)},...,y^{(\tau )}),(5) \\ =\sum L^{(t)}(6) \end{gathered}$$

2.2计算循环神经网络的梯度

梯度计算涉及执行一次前向传播（如在Fig.1展开图中从左到右的传播），接着是由右到左的反向传播。运行时间是O(τ)，并且不能通过并行化来降低，因为前向传播图是固有循序的;每个时间步只能一前一后地计算。前向传播中的各个状态必须保存，直到它们反向传播中被再次使用，因此内存代价也是O(τ)。应用于展开图且代价为O(τ) 的反向传播算法称为通过时间反向传播（back-propagation through time, BPTT）。
计算循环神经网络的梯度是容易的。我们可以简单地将反向传播算法应用于展开的计算图，而不需要特殊化的算法。由反向传播计算得到的梯度，并结合任何通用的基于梯度的技术就可以训练RNN。
为了获得BPTT 算法行为一些直观理解，我们举例说明如何通过BPTT 计算上述RNN公式（式(1) 和式(5)）的梯度。计算图的节点包括参数U， V， W， b和c，以及以t 为索引的节点序列$x^{(t)},h^{(t)},o^{(t)}和L^{(t)}$。对于每一个节点N，我们需要基于N 后面的节点的梯度，递归地计算梯度${\nabla }_{N}L$。我们从紧接着最终损失的节点开始递归：
$$\frac{\partial L}{\partial L^{(t)}}=1(7)$$
在这个导数中，我们假设输出$o^{(t)}$ 作为softmax 函数的参数，我们可以从softmax函数可以获得关于输出概率的向量^y。我们也假设损失是迄今为止给定了输入后的真实目标$y^{(t)}$ 的负对数似然。对于所有i,t，关于时间步t 输出的梯度${\nabla }_{o^{(t)}}L$如下:

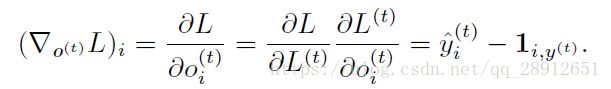
我们从序列的末尾开始，反向进行计算。在最后的时间步τ , $h^{(\tau )}$只有$o^{(\tau )}$作为后续节点，因此这个梯度很简单：

然后，我们可以从时刻 t = τ - 1 到 t = 1 反向迭代，通过时间反向传播梯度，注意$h^{(t)}$(t < τ) 同时具有$o^{(t)}$和$h^{(t+1)}$两个后续节点。因此，它的梯度由下式计算

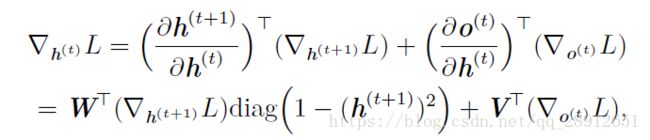
其中$diag(1-(h^{(t+1)}{)}^2)$表示包含元素$1-(h_i^{(t+1)}{)}^2$的对角矩阵。这是关于时刻 t+1 与隐藏单元 i 关联的双曲正切的Jacobian。
一旦获得了计算图内部节点的梯度，我们就可以得到关于参数节点的梯度。因为参数在许多时间步共享，我们必须在表示这些变量的微积分操作时谨慎对待。然而微积分中的${\nabla }_{W}f$算子，计算W对于f 的贡献时将计算图中的所有边都考虑进去了。为了消除这种歧义，我们定义只在t 时刻使用的虚拟变量$W^{(t)}$ 作为W的副本。然后，我们可以使用${\nabla }_{W^{(t)}}$ 表示权重在时间步t 对梯度的贡献。
使用这个表示，关于剩下参数的梯度可以由下式给出：

因为计算图中定义的损失的任何参数都不是训练数据$x^{(t)}$ 的父节点，所以我们不需要计算关于它的梯度。

3.TensorFlow实现

TensorFlow支持RNN的各种变体，可从tf.nn.rnn_cell模块中找到这些变体的实现。可以借助tensorflow.models.rnn中的tf.nn.dynamic_rnn()运算。
关于参数，dynamic_rnn()接收一个循环网络的定义以及若干输入序列构成的批数据。就目前而言，所有的序列都是等长的。该函数会向数据流图创建RNN所需的计算，并返回保存了每个时间步的输出和隐含状态的两个张量。

import tensorflow as tf 
from tensorflow.models.rnn import rnn_cell
from tensorflow.models.rnn import rnn

#输出数据的维数：batch_size * sequence_length *frame_size.
#不限制批次大小，将第一维尺寸设为None
sequence_length = ...
frame_size = ...
data = tf.placeholder(tf.float32. [None, sequence_length, frame_size])

num_neurons = ...
network = rnn_cell.BasicRNNCell(num_neurons)

#为sequence_length步定义模拟RNN的运算
outputs, states = rnn.dynamic_rnn(network, data,
dtype=tf.float32)

这样便完成了RNN的定义，并将它沿时间轴展开，只需要加载一些数据并选择一种TensorFlow的优化器，如tf.train.RMSPropOptimizer或tf.train.AdamOptimizer训练网络即可。

4.后续优化

本文仍存在以下几点问题：

1. 激活函数选择的双曲正弦，可以优化为ReLu函数，具体优劣请自行百度；
2. RNN自身会出现梯度消散等许多问题，所以有很多变种与优化，下文会着重讲LSTM的原理与TensorFlow实现。