区块链:密码学与安全技术
工程领域从来没有黑科技;密码学不仅是工程。
密码学为核心的安全技术在信息科技领域的重要性无需多言。离开现代密码学和信息安全技术,人类社会将无法全面步入信息时代。区块链和分布式账本中大量使用了密码学和安全技术的最新成果,特别是身份认证和隐私保护相关技术。
从数学定理到工程实践,密码学和信息安全所涉及的知识体系十分繁杂。本章将介绍跟区块链密切相关的安全知识,包括 Hash 算法与摘要、加密算法、数字签名和证书、PKI 体系、Merkle 树、布隆过滤器、同态加密等。通过学习,读者可以了解常见安全技术体系,以及如何实现信息安全的核心要素:机密性、完整性、可认证性和不可抵赖性,为后续理解区块链的设计奠定基础。
密码学简史
从历史角度看,密码学可以大致分为古典密码学和近现代密码学两个阶段。两者以现代信息技术的诞生为分界点,现在所讨论的密码学多是指后者,建立在信息论和数学成果基础之上。
古典密码学源自数千年前。最早在公元前 1900 年左右的古埃及,就出现过使用特殊字符和简单替换式密码来保护信息。美索不达米亚平原上曾出土一个公元前 1500 年左右的泥板,其上记录了加密描述的陶器上釉工艺配方。古希腊时期(公元前 800 ~ 前 146 年)还发明了通过物理手段来隐藏信息的“隐写术”,例如使用牛奶书写、用蜡覆盖文字等。后来在古罗马时期还出现了基于替换加密的凯撒密码,据称凯撒曾用此方法与其部下通信而得以命名。
这些手段多数是采用简单的机械工具来保护秘密,在今天看来毫无疑问是十分简陋,很容易破解的。严格来看,可能都很难称为密码科学。
近现代密码的研究源自第一、二次世界大战中对军事通信进行保护和破解的需求。
1901 年 12 月,意大利工程师 Guglielmo Marconi(奎里亚摩·马可尼)成功完成了跨越大西洋的无线电通信实验,在全球范围内引发轰动,推动了无线电通信时代的带来。无线电极大提高了远程通信的能力,但存在着天然缺陷——它很难限制接收方,这意味着要想保护所传递信息的安全,必须采用可靠的加密技术。
对无线电信息进行加密以及破解的过程直接促进了近现代密码学和计算机技术的出现。反过来,这些科技进步也影响了时代的发展。一战时期德国外交部长 Arthur Zimmermann(阿瑟·齐默尔曼)拉拢墨西哥构成抗美军事同盟的电报(1917 年 1 月 16 日)被英国情报机构 —— 40 号办公室破译,直接导致了美国的参战;二战时期德国使用的恩尼格玛(Enigma)密码机(当时最先进的加密设备)被盟军成功破译(1939 年到 1941 年),导致大西洋战役德国失败。据称,二战时期光英国从事密码学研究的人员就达到 7000 人,而他们的成果使二战结束的时间至少提前了一到两年时间。
1945 年 9 月 1 日,Claude Elwood Shannon(克劳德·艾尔伍德·香农)完成了划时代的内部报告《A Mathematical Theory of Cryptography(密码术的一个数学理论)》,1949 年 10 月,该报告以《Communication Theory of Secrecy Systems(保密系统的通信理论)》为题在 Bell System Technical Journal(贝尔系统技术期刊)上正式发表。这篇论文首次将密码学和信息论联系到一起,为对称密码技术提供了数学基础。这也标志着近现代密码学的正式建立。
1976 年 11 月,Whitfield Diffie 和 Martin E.Hellman 在 IEEE Transactions on Information Theory 上发表了论文《New Directions in Cryptography(密码学的新方向)》,探讨了无需传输密钥的保密通信和签名认证体系问题,正式开创了现代公钥密码学体系的研究。
现代密码学的发展与电气技术特别计算机信息理论和技术关系密切,已经发展为包括随机数、Hash 函数、加解密、身份认证等多个课题的庞大领域,相关成果为现代信息系统特别互联网奠定了坚实的安全基础。
注:Enigma 密码机的加密消息在当年需要数年时间才能破解,而今天使用最新的人工智能技术进行破译只需要 10 分钟左右。
Hash 算法与数字摘要
定义
Hash(哈希或散列)算法,又常被称为指纹(fingerprint)或摘要(digest)算法,是非常基础也非常重要的一类算法。可以将任意长度的二进制明文串映射为较短的(通常是固定长度的)二进制串(Hash 值),并且不同的明文很难映射为相同的 Hash 值。
例如计算 “hello blockchain world, this is yeasy@github” 的 SHA-256 Hash 值。
$ echo "hello blockchain world, this is yeasy@github"|shasum -a 256
db8305d71a9f2f90a3e118a9b49a4c381d2b80cf7bcef81930f30ab1832a3c90
对于某个文件,无需查看其内容,只要其 SHA-256 Hash 计算后结果同样为 db8305d71a9f2f90a3e118a9b49a4c381d2b80cf7bcef81930f30ab1832a3c90,则说明文件内容(极大的概率)就是 “hello blockchain world, this is yeasy@github”。
除了快速对比内容外,Hash 思想也经常被应用到基于内容的编址或命名算法中。
一个优秀的 Hash 算法,将能满足:
- 正向快速:给定原文和 Hash 算法,在有限时间和有限资源内能计算得到 Hash 值;
- 逆向困难:给定(若干)Hash 值,在有限时间内无法(基本不可能)逆推出原文;
- 输入敏感:原始输入信息发生任何改变,新产生的 Hash 值都应该发生很大变化;
- 碰撞避免:很难找到两段内容不同的明文,使得它们的 Hash 值一致(即发生碰撞)。
碰撞避免有时候又被称为“抗碰撞性”,可分为“弱抗碰撞性”和“强抗碰撞性”。给定原文前提下,无法找到与之碰撞的其它原文,则算法具有“弱抗碰撞性”;更一般地,如果无法找到任意两个可碰撞的原文,则称算法具有“强抗碰撞性”。
很多场景下,也往往要求算法对于任意长的输入内容,输出为定长的 Hash 结果。
常见算法
目前常见的 Hash 算法包括国际上的 Message Digest(MD)系列和 Secure Hash Algorithm(SHA)系列算法,以及国内的 SM3 算法。
MD 算法主要包括 MD4 和 MD5 两个算法。MD4(RFC 1320)是 MIT 的 Ronald L. Rivest 在 1990 年设计的,其输出为 128 位。MD4 已证明不够安全。MD5(RFC 1321)是 Rivest 于 1991 年对 MD4 的改进版本。它对输入仍以 512 位进行分组,其输出是 128 位。MD5 比 MD4 更加安全,但过程更加复杂,计算速度要慢一点。MD5 已于 2004 年被成功碰撞,其安全性已不足应用于商业场景。。
SHA 算法由美国国家标准与技术院(National Institute of Standards and Technology,NIST)征集制定。首个实现 SHA-0 算法于 1993 年问世,1998 年即遭破解。随后的修订版本 SHA-1 算法在 1995 年面世,它的输出为长度 160 位的 Hash 值,安全性更好。SHA-1 设计采用了 MD4 算法类似原理。SHA-1 已于 2005 年被成功碰撞,意味着无法满足商用需求。
为了提高安全性,NIST 后来制定出更安全的 SHA-224、SHA-256、SHA-384,和 SHA-512 算法(统称为 SHA-2 算法)。新一代的 SHA-3 相关算法也正在研究中。
此外,中国密码管理局于 2010 年 12 月 17 日发布了GM/T 0004-2012 《SM3 密码杂凑算法》,建立了国内商用密码体系中的公开 Hash 算法标准,已经被广泛应用在数字签名和认证等场景中。
注:MD5 和 SHA-1 算法的破解工作都是由清华大学教授、中国科学院院士王小云主导完成。
性能
大多数 Hash 算法都是计算敏感型算法,在强大的计算芯片上完成的更快。因此要提升 Hash 计算的性能可以考虑硬件加速。例如采用普通 FPGA 来计算 SHA-256 值,可以轻易达到数 Gbps 的吞吐量,使用专用芯片甚至会更高。
也有一些 Hash 算法不是计算敏感型的。例如 scrypt算法,计算过程需要大量的内存资源,因此很难通过选用高性能芯片来加速 Hash 计算。这样的算法可以有效防范采用专用芯片进行算力攻击。
数字摘要
数字摘要是 Hash 算法重要用途之一。顾名思义,数字摘要是对原始的数字内容进行 Hash 运算,获取唯一的摘要值。
利用 Hash 函数抗碰撞性特点,数字摘要可以检测内容是否被篡改过。
细心的读者可能会注意到,有些网站在提供文件下载时,会同时提供相应的数字摘要值。用户下载原始文件后可以在本地自行计算摘要值,并与所提供摘要值进行比对,以确保文件内容没有被篡改过。
Hash 攻击与防护
Hash 算法并不是一种加密算法,不能用于对信息的保护。
但 Hash 算法可被应用到对登录口令的保存上。例如网站登录时需要验证用户名和密码,如果网站后台直接保存用户的口令原文,一旦发生数据库泄露后果不堪设想(事实上,网站数据库泄露事件在国内外都不少见)。
利用 Hash 的防碰撞特性,后台数据库可以仅保存用户口令的 Hash 值,这样每次通过 Hash 值比对,即可判断输入口令是否正确。即便数据库泄露了,攻击者也无法轻易从 Hash 值还原回口令。
然而,有时用户设置口令的安全强度不够,采用了一些常见的字符串,如 password、123456 等。有人专门搜集了这些常见口令,计算对应的 Hash 值,制作成字典。这样通过 Hash 值可以快速反查到原始口令。这一类型以空间换时间的攻击方法包括字典攻击和彩虹表攻击(只保存一条 Hash 链的首尾值,相对字典攻击可以节省存储空间)等。
为了防范这一类攻击,可以采用加盐(Salt)的方法。保存的不是原文的直接 Hash 值,而是原文再加上一段随机字符串(即“盐”)之后的 Hash 值。Hash 结果和“盐”分别存放在不同的地方,这样只要不是两者同时泄露,攻击者很难进行破解。
加解密算法
加解密算法是现代密码学核心技术,从设计理念和应用场景上可以分为两大基本类型,如下表所示。
| 算法类型 | 特点 | 优势 | 缺陷 | 代表算法 |
|---|---|---|---|---|
| 对称加密 | 加解密的密钥相同 | 计算效率高,加密强度高 | 需提前共享密钥,易泄露 | DES、3DES、AES、IDEA |
| 非对称加密 | 加解密的密钥不相同 | 无需提前共享密钥 | 计算效率低,存在中间人攻击可能 | RSA、ElGamal、椭圆曲线算法 |
加解密系统基本组成
现代加解密系统的典型组件包括算法和密钥(包括加密密钥、解密密钥)。
其中,加解密算法自身是固定不变的,并且一般是公开可见的;密钥则是最关键的信息,需要安全地保存起来,甚至通过特殊硬件进行保护。一般来说,密钥需要在加密前按照特定算法随机生成,长度越长,则加密强度越大。
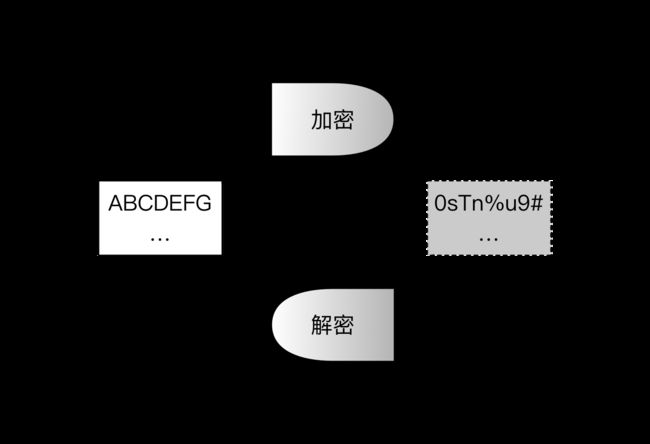
加解密的典型过程如下图所示。加密过程中,通过加密算法和加密密钥,对明文进行加密,获得密文;解密过程中,通过解密算法和解密密钥,对密文进行解密,获得明文。
图 1.8.3.1 - 加解密的基本过程
根据加解密过程中所使用的密钥是否相同,算法可以分为对称加密(Symmetric Cryptography,又称共有密钥加密,Common-key cryptography)和非对称加密(Asymmetric Cryptography,又称公钥加密,Public-key Cryptography)。两种模式适用于不同的需求,形成互补。某些场景下可以组合使用,形成混合加密机制。
对称加密算法
对称加密算法,顾名思义,加密和解密过程的密钥是相同的。
该类算法优点是加解密效率(速度快,空间占用小)和加密强度都很高。
缺点是参与方需要提前持有密钥,一旦有人泄露则系统安全性被破坏;另外如何在不安全通道中提前分发密钥也是个问题,需要借助额外的 Diffie–Hellman 协商协议或非对称加密算法来实现。
对称密码从实现原理上可以分为两种:分组密码和序列密码。前者将明文切分为定长数据块作为基本加密单位,应用最为广泛。后者则每次只对一个字节或字符进行加密处理,且密码不断变化,只用在一些特定领域(如数字媒介的加密)。
分组对称加密代表算法包括 DES、3DES、AES、IDEA 等。
- DES(Data Encryption Standard):经典的分组加密算法,最早是 1977 年美国联邦信息处理标准(FIPS)采用 FIPS-46-3,将 64 位明文加密为 64 位的密文。其密钥长度为 64 位(包括 8 位校验码),现在已经很容易被暴力破解;
- 3DES:三重 DES 操作:加密 --> 解密 --> 加密,处理过程和加密强度优于 DES,但现在也被认为不够安全;
- AES(Advanced Encryption Standard):由美国国家标准研究所(NIST)采用,取代 DES 成为对称加密实现的标准,1997~2000 年 NIST 从 15 个候选算法中评选 Rijndael 算法(由比利时密码学家 Joan Daemon 和 Vincent Rijmen 发明)作为 AES,标准为 FIPS-197。AES 也是分组算法,分组长度为 128、192、256 位三种。AES 的优势在于处理速度快,整个过程可以数学化描述,目前尚未有有效的破解手段;
- IDEA(International Data Encryption Algorithm):1991 年由密码学家 James Massey 与来学嘉共同提出。设计类似于 3DES,密钥长度增加到 128 位,具有更好的加密强度。
序列加密,又称流加密。1949 年,Claude Elwood Shannon(信息论创始人)首次证明,要实现绝对安全的完善保密性(Perfect Secrecy),可以通过“一次性密码本”的对称加密处理。即通信双方每次使用跟明文等长的随机密钥串对明文进行加密处理。序列密码采用了类似的思想,每次通过伪随机数生成器来生成伪随机密钥串。代表算法包括 RC4 等。
总结下,对称加密算法适用于大量数据的加解密过程;不能用于签名场景;并且需要提前安全地分发密钥。
注:分组加密每次只能处理固定长度的明文,因此对于过长的内容需要采用一定模式进行分割,《实用密码学》一书中推荐使用密文分组链(Cipher Block Chain,CBC)、计数器(Counter,CTR)等模式。
非对称加密算法
非对称加密是现代密码学的伟大发明,它有效解决了对称加密需要安全分发密钥的问题。
顾名思义,非对称加密中,加密密钥和解密密钥是不同的,分别被称为公钥(Public Key)和私钥(Private Key)。私钥一般通过随机数算法生成,公钥可以根据私钥生成。
其中,公钥一般是公开的,他人可获取的;私钥则是个人持有并且要严密保护,不能被他人获取。
非对称加密算法优点是公私钥分开,无需安全通道来分发密钥。缺点是处理速度(特别是生成密钥和解密过程)往往比较慢,一般比对称加解密算法慢 2~3 个数量级;同时加密强度也往往不如对称加密。
非对称加密算法的安全性往往基于数学问题,包括大数质因子分解、离散对数、椭圆曲线等经典数学难题。
代表算法包括:RSA、ElGamal、椭圆曲线(Elliptic Curve Crytosystems,ECC)、SM2 等系列算法。
- RSA:经典的公钥算法,1978 年由 Ron Rivest、Adi Shamir、Leonard Adleman 共同提出,三人于 2002 年因此获得图灵奖。算法利用了对大数进行质因子分解困难的特性,但目前还没有数学证明两者难度等价,或许存在未知算法可以绕过大数分解而进行解密。
- ElGamal:由 Taher ElGamal 设计,利用了模运算下求离散对数困难的特性,比 RSA 产生密钥更快。被应用在 PGP 等安全工具中。
- 椭圆曲线算法(Elliptic Curve Cryptography,ECC):应用最广也是强度最早的系列算法,基于对椭圆曲线上特定点进行特殊乘法逆运算(求离散对数)难以计算的特性。最早在 1985 年由 Neal Koblitz 和 Victor Miller 分别独立提出。ECC 系列算法具有多种国际标准(包括 ANSI X9.63、NIST FIPS 186-2、IEEE 1363-2000、ISO/IEC 14888-3 等),一般被认为具备较高的安全性,但加解密过程比较费时。其中,密码学家 Daniel J.Bernstein 于 2006 年提出的 Curve25519/Ed25519/X25519 等算法(分别解决加密、签名和密钥交换),由于其设计完全公开、性能突出等特点,近些年引起了广泛关注和应用。
- SM2(ShangMi 2):中国国家商用密码系列算法标准,由中国密码管理局于 2010 年 12 月 17 日发布,同样基于椭圆曲线算法,一般认为其安全强度优于 RSA 系列算法。
非对称加密算法适用于签名场景或密钥协商过程,但不适于大量数据的加解密。除了 SM2 之外,大部分算法的签名速度要比验签速度慢(1~2个数量级)。
RSA 类算法被认为已经很难抵御现代计算设备的破解,一般推荐商用场景下密钥至少为 2048 位。如果采用安全强度更高的椭圆曲线算法,256 位密钥即可满足绝大部分安全需求。
选择明文攻击
细心的读者可能会想到,非对称加密中公钥是公开的,因此任何人都可以利用它加密给定明文,获取对应的密文,这就带来选择明文攻击的风险。
为了规避这种风险,现代的非对称加密算法(如 RSA、ECC)都引入了一定的保护机制:对同样的明文使用同样密钥进行多次加密,得到的结果完全不同,这就避免了选择明文攻击的破坏。
在实现上可以有多种思路。一种是对明文先进行变形,添加随机的字符串或标记,再对添加后结果进行处理。另外一种是先用随机生成的临时密钥对明文进行对称加密,然后再将对称密钥进行加密,即利用多层加密机制。
混合加密机制
混合加密机制同时结合了对称加密和非对称加密的优点。
该机制的主要过程为:先用非对称加密(计算复杂度较高)协商出一个临时的对称加密密钥(或称会话密钥),然后双方再通过对称加密算法(计算复杂度较低)对所传递的大量数据进行快速的加密处理。
典型的应用案例是网站中使用越来越普遍的通信协议 -- 安全超文本传输协议(Hyper Text Transfer Protocol Secure,HTTPS)。
与以明文方式传输数据的 HTTP 协议不同,HTTPS 在传统的 HTTP 层和 TCP 层之间引入 Transport Layer Security/Secure Socket Layer(TLS/SSL)加密层来实现安全传输。
SSL 协议是HTTPS 初期采用的标准协议,最早由 Netscape 于 1994 年设计实现,其两个主要版本(包括 v2.0 和 v3.0)曾得到大量应用。SSL 存在安全缺陷易受攻击(如 POODLE 和 DROWN 攻击),无法满足现代安全需求,已于 2011 和 2015 年被 IETF 宣布废弃。基于 SSL 协议(v3.1),IETF 提出了改善的安全标准协议 TLS,成为目前广泛采用的方案。2008 年 8 月,TLS 1.2 版本(RFC 5246)发布,修正了之前版本的不少漏洞,极大增强了安全性;2018 年 8 月,TLS 1.3 版本(RFC 8446)发布,提高了握手性能同时增强了安全性。商用场景推荐使用这两个版本。除了 Web 服务外,TLS 协议也被广泛应用到 FTP、Email、实时消息、音视频通话等场景中。
采用 HTTPS 建立安全连接(TLS 握手协商过程)的基本步骤如下:
图 1.8.3.2 - TLS 握手协商过程
- 客户端浏览器发送握手信息到服务器,包括随机数 R1、支持的加密算法套件(Cipher Suite)类型、协议版本、压缩算法等。注意该过程传输为明文。
- 服务端返回信息,包括随机数 R2、选定加密算法套件、协议版本,以及服务器证书。注意该过程为明文。
- 浏览器检查带有该网站公钥的证书。该证书需要由第三方 CA 来签发,浏览器和操作系统会预置权威 CA 的根证书。如果证书被篡改作假(中间人攻击),很容易通过 CA 的证书验证出来。
- 如果证书没问题,则客户端用服务端证书中公钥加密随机数 R3(又叫 Pre-MasterSecret),发送给服务器。此时,只有客户端和服务器都拥有 R1、R2 和 R3 信息,基于随机数 R1、R2 和 R3,双方通过伪随机数函数来生成共同的对称会话密钥 MasterSecret。
- 后续客户端和服务端的通信都通过协商后的对称加密(如 AES)进行保护。
可以看出,该过程是实现防止中间人窃听和篡改的前提下完成会话密钥的交换。为了保障前向安全性(Perfect Forward Secrecy),TLS 对每个会话连接都可以生成不同的密钥,避免某个会话密钥泄露后对其它会话连接产生安全威胁。需要注意,选用合适的加密算法套件对于 TLS 的安全性十分重要。要合理选择安全强度高的算法组合,如 ECDHE-RSA 和 ECDHE-ECDSA 等,而不要使用安全性较差的 DES/3DES 等。
示例中对称密钥的协商过程采用了 RSA 非对称加密算法,实践中也可以通过 Diffie–Hellman(DH)协议来完成。
加密算法套件包括一组算法,包括交换、认证、加密、校验等。
- 密钥交换算法:负责协商对称密钥,常见类型包括 RSA、DH、ECDH、ECDHE 等;
- 证书签名算法:负责验证身份,常见类型包括 RSA、DSA、ECDSA 等;
- 加密数据算法:对建立连接的通信内容进行对称加密,常见类型包括 AES 等;
- 消息认证信息码(MAC)算法:创建报文摘要,验证消息的完整性,常见类型包括 SHA 等。
一个典型的 TLS 密码算法套件可能为 “TLS_ECDHE_ECDSA_WITH_AES_256_CBC_SHA384”,意味着:
- 协商过程算法是 ECDHE(Elliptic Curve Diffie–Hellman Ephemeral),基于椭圆曲线的短期 EH 交换,每次交换都用新的密钥,保障前向安全性;
- 证书签名算法是 ECDSA(Elliptic Curve Digital Signature Algorithm),基于椭圆曲线的签名;
- 加密数据算法是 AES,密钥的长度和初始向量的长度都是 256,模式是 CBC;
- 消息认证信息码算法是 SHA,结果是 384 位。
目前,推荐选用如下的加密算法套件:
- TLS_ECDHE_ECDSA_WITH_AES_256_GCM_SHA384
- TLS_ECDHE_RSA_WITH_AES_256_GCM_SHA384
- TLS_RSA_WITH_AES_256_GCM_SHA384
- TLS_ECDH_ECDSA_WITH_AES_256_GCM_SHA384
- TLS_ECDH_RSA_WITH_AES_256_GCM_SHA384
- TLS_DHE_RSA_WITH_AES_256_GCM_SHA384
注:TLS 1.0 版本已被发现存在安全漏洞,NIST、HIPAA 于 2014 年公开建议停用该版本的 TLS 协议。
离散对数与 Diffie–Hellman 密钥交换协议
Diffie–Hellman(DH)密钥交换协议是一个应用十分广泛的协议,最早由惠特菲尔德·迪菲(Bailey Whitfield Diffie)和马丁·赫尔曼(Martin Edward Hellman)于 1976 年提出。该协议可以实现在不安全信道中协商对称密钥。
DH 协议的设计基于著名的离散对数问题(Discrete Logarithm Problem,DLP)。离散对数问题是指对于一个很大的素数 p,已知 g 为 p 的模循环群的原根,给定任意 x,求解 X=g^x mod p 是可以很快获取的。但在已知 p,g 和 X 的前提下,逆向求解 x 很难(目前没有找到多项式时间实现的算法)。该问题同时也是 ECC 类加密算法的基础。
DH 协议的基本交换过程如下,以 Alice 和 Bob 两人协商为例:
- Alice 和 Bob 两个人协商密钥,先公开商定 p,g;
- Alice 自行选取私密的整数 x,计算 X=g^x mod p,发送 X 给 Bob;
- Bob 自行选取私密的整数 y,计算 Y=g^y mod p,发送 Y 给 A;
- Alice 根据 x 和 Y,求解共同密钥 Z_A=Y^x mod p;
- Bob 根据 X 和 y,求解共同密钥 Z_B=X^y mod p。
实际上,Alice 和 Bob 计算出来的结果将完全相同,因为在 mod p 的前提下,Y^x =(g^y)^x =g^(xy) = (g^x)^y=X^y。而信道监听者在已知 p,g,X,Y 的前提下,无法求得 Z。
安全性
虽然很多加密算法的安全性建立在数学难题基础之上,但并非所有算法的安全性都可以从数学上得到证明。
公认高安全的加密算法和实现往往是经过长时间充分实践论证后,才被大家所认可,但不代表其绝对不存在漏洞。使用方式和参数不当,也会造成安全强度的下降。
另一方面,自行设计和发明未经过大规模验证的加密算法是一种不太明智的行为。即便不公开算法加密过程,也很容易被分析和攻击,无法在安全性上得到足够保障。
实际上,现代密码学算法的安全性是通过数学难题来提供的,并非通过对算法自身的实现过程进行保密。
消息认证码与数字签名
消息认证码和数字签名技术通过对消息的摘要进行加密,可以防止消息被篡改和认证身份。
消息认证码
消息认证码(Hash-based Message Authentication Code,HMAC),利用对称加密,对消息完整性(Integrity)进行保护。
基本过程为对某个消息,利用提前共享的对称密钥和 Hash 算法进行处理,得到 HMAC 值。该 HMAC 值持有方可以向对方证明自己拥有某个对称密钥,并且确保所传输消息内容未被篡改。
典型的 HMAC 生成算法包括 K,H,M 三个参数。K 为提前共享的对称密钥,H 为提前商定的 Hash 算法(如 SHA-256),M 为要传输的消息内容。三个参数缺失了任何一个,都无法得到正确的 HMAC 值。
消息认证码可以用于简单证明身份的场景。如 Alice、Bob 提前共享了 K 和 H。Alice 需要知晓对方是否为 Bob,可发送一段消息 M 给 Bob。Bob 收到 M 后计算其 HMAC 值并返回给 Alice,Alice 检验收到 HMAC 值的正确性可以验证对方是否真是 Bob。
注:例子中并没有考虑中间人攻击的情况,并假定信道是安全的。
消息认证码的主要问题是需要提前共享密钥,并且当密钥可能被多方同时拥有(甚至泄露)的场景下,无法追踪消息的真实来源。如果采用非对称加密算法,则能有效的解决这个问题,即数字签名。
数字签名
类似在纸质合同上进行签名以确认合同内容和证明身份,数字签名既可以证实某数字内容的完整性,又可以确认其来源(即不可抵赖,Non-Repudiation)。
一个典型的场景是,Alice 通过信道发给 Bob 一个文件(一份信息),Bob 如何获知所收到的文件即为 Alice 发出的原始版本?Alice 可以先对文件内容进行摘要,然后用自己的私钥对摘要进行加密(签名),之后同时将文件和签名都发给 Bob。Bob 收到文件和签名后,用 Alice 的公钥来解密签名,得到数字摘要,与对文件进行摘要后的结果进行比对。如果一致,说明该文件确实是 Alice 发过来的(因为别人无法拥有 Alice 的私钥),并且文件内容没有被修改过(摘要结果一致)。
理论上所有的非对称加密算法都可以用来实现数字签名,实践中常用算法包括 1991 年 8 月 NIST 提出的 DSA(Digital Signature Algorithm,基于 ElGamal 算法)和安全强度更高的 ECSDA(Elliptic Curve Digital Signature Algorithm,基于椭圆曲线算法)等。
除普通的数字签名应用场景外,针对一些特定的安全需求,产生了一些特殊数字签名技术,包括盲签名、多重签名、群签名、环签名等。
盲签名
盲签名(Blind Signature),1982 年由 David Chaum 在论文《Blind Signatures for Untraceable Payment》中提出。签名者需要在无法看到原始内容的前提下对信息进行签名。
盲签名可以实现对所签名内容的保护,防止签名者看到原始内容;另一方面,盲签名还可以实现防止追踪(Unlinkability),签名者无法将签名内容和签名结果进行对应。典型的实现包括 RSA 盲签名算法等。
多重签名
多重签名(Multiple Signature),即 n 个签名者中,收集到至少 m 个(n >= m >= 1)的签名,即认为合法。
其中,n 是提供的公钥个数,m 是需要匹配公钥的最少的签名个数。
多重签名可以有效地被应用在多人投票共同决策的场景中。例如双方进行协商,第三方作为审核方。三方中任何两方达成一致即可完成协商。
比特币交易中就支持多重签名,可以实现多个人共同管理某个账户的比特币交易。
群签名
群签名(Group Signature),即某个群组内一个成员可以代表群组进行匿名签名。签名可以验证来自于该群组,却无法准确追踪到签名的是哪个成员。
群签名需要存在一个群管理员来添加新的群成员,因此存在群管理员可能追踪到签名成员身份的风险。
群签名最早在 1991 年由 David Chaum 和 Eugene van Heyst 提出。
环签名
环签名(Ring Signature),由 Rivest,Shamir 和 Tauman 三位密码学家在 2001 年首次提出。环签名属于一种简化的群签名。
签名者首先选定一个临时的签名者集合,集合中包括签名者自身。然后签名者利用自己的私钥和签名集合中其他人的公钥就可以独立的产生签名,而无需他人的帮助。签名者集合中的其他成员可能并不知道自己被包含在最终的签名中。
环签名在保护匿名性方面也具有很多用途。
安全性
数字签名算法自身的安全性由数学问题进行保护。但在实践中,各个环节的安全性都十分重要,一定要严格遵循标准流程。
例如,目前常见的数字签名算法需要选取合适的随机数作为配置参数,配置参数不合理的使用或泄露都会造成安全漏洞和风险。
2010 年 8 月,SONY 公司因为其 PS3 产品上采用十分安全的 ECDSA 进行签名时,不慎采用了重复的随机参数,导致私钥被最终破解,造成重大经济损失。
数字证书
对于非对称加密算法和数字签名来说,很重要的步骤就是公钥的分发。理论上任何人都可以获取到公开的公钥。然而这个公钥文件有没有可能是伪造的呢?传输过程中有没有可能被篡改呢?一旦公钥自身出了问题,则整个建立在其上的的安全性将不复成立。
数字证书机制正是为了解决这个问题,它就像日常生活中的证书一样,可以确保所记录信息的合法性。比如证明某个公钥是某个实体(个人或组织)拥有,并且确保任何篡改都能被检测出来,从而实现对用户公钥的安全分发。
根据所保护公钥的用途,数字证书可以分为加密数字证书(Encryption Certificate)和签名验证数字证书(Signature Certificate)。前者往往用于保护用于加密用途的公钥;后者则保护用于签名用途的公钥。两种类型的公钥也可以同时放在同一证书中。
一般情况下,证书需要由证书认证机构(Certification Authority,CA)来进行签发和背书。权威的商业证书认证机构包括 DigiCert、GlobalSign、VeriSign 等。用户也可以自行搭建本地 CA 系统,在私有网络中进行使用。
X.509 证书规范
一般的,一个数字证书内容可能包括证书域(证书的版本、序列号、签名算法类型、签发者信息、有效期、被签发主体、签发的公开密钥)、CA 对证书的签名算法和签名值等。
目前使用最广泛的标准为 ITU 和 ISO 联合制定的 X.509 的 v3 版本规范(RFC 5280),其中定义了如下证书信息域:
- 版本号(Version Number):规范的版本号,目前为版本 3,值为 0x2;
- 序列号(Serial Number):由 CA 维护的为它所颁发的每个证书分配的唯一的序列号,用来追踪和撤销证书。只要拥有签发者信息和序列号,就可以唯一标识一个证书。最大不能超过 20 个字节;
- 签名算法(Signature Algorithm):数字签名所采用的算法,如 sha256WithRSAEncryption 或 ecdsa-with-SHA256;
- 颁发者(Issuer):颁发证书单位的信息,如 “C=CN, ST=Beijing, L=Beijing, O=org.example.com, CN=ca.org.example.com”;
- 有效期(Validity):证书的有效期限,包括起止时间(如 Not Before 2018-08-08-00-00UTC,Not After 2028-08-08-00-00UTC);
- 被签发主体(Subject):证书拥有者的标识信息(Distinguished Name),如 “C=CN, ST=Beijing, L=Beijing, CN=personA.org.example.com”;
- 主体的公钥信息(Subject Public Key Info):所保护的公钥相关的信息;
- 公钥算法(Public Key Algorithm):公钥采用的算法;
- 主体公钥(Subject Public Key):公钥的内容;
- 颁发者唯一号(Issuer Unique Identifier,可选):代表颁发者的唯一信息,仅 2、3 版本支持,可选;
- 主体唯一号(Subject Unique Identifier,可选):代表拥有证书实体的唯一信息,仅 2、3 版本支持,可选;
- 扩展(Extensions,可选):可选的一些扩展。可能包括:
- Subject Key Identifier:实体的密钥标识符,区分实体的多对密钥;
- Basic Constraints:一般指明该证书是否属于某个 CA;
- Authority Key Identifier:颁发这个证书的颁发者的公钥标识符;
- Authority Information Access:颁发相关的服务地址,如颁发者证书获取地址和吊销证书列表信息查询地址;
- CRL Distribution Points:证书注销列表的发布地址;
- Key Usage: 表明证书的用途或功能信息,如 Digital Signature、Key CertSign;
- Subject Alternative Name:证书身份实体的别名,如该证书可以同样代表 .org.example.com,org.example.com,.example.com,example.com 身份等。
此外,证书的颁发者还需要对证书内容利用自己的私钥进行签名,以防止他人篡改证书内容。
证书格式
X.509 规范中一般推荐使用 PEM(Privacy Enhanced Mail)格式来存储证书相关的文件。证书文件的文件名后缀一般为 .crt 或 .cer,对应私钥文件的文件名后缀一般为 .key,证书请求文件的文件名后缀为 .csr。有时候也统一用 .pem 作为文件名后缀。
PEM 格式采用文本方式进行存储,一般包括首尾标记和内容块,内容块采用 base64 编码。
例如,一个示例证书文件的 PEM 格式如下所示。
-----BEGIN CERTIFICATE-----
MIICMzCCAdmgAwIBAgIQIhMiRzqkCljq3ZXnsl6EijAKBggqhkjOPQQDAjBmMQsw
CQYDVQQGEwJVUzETMBEGA1UECBMKQ2FsaWZvcm5pYTEWMBQGA1UEBxMNU2FuIEZy
YW5jaXNjbzEUMBIGA1UEChMLZXhhbXBsZS5jb20xFDASBgNVBAMTC2V4YW1wbGUu
Y29tMB4XDTE3MDQyNTAzMzAzN1oXDTI3MDQyMzAzMzAzN1owZjELMAkGA1UEBhMC
VVMxEzARBgNVBAgTCkNhbGlmb3JuaWExFjAUBgNVBAcTDVNhbiBGcmFuY2lzY28x
FDASBgNVBAoTC2V4YW1wbGUuY29tMRQwEgYDVQQDEwtleGFtcGxlLmNvbTBZMBMG
ByqGSM49AgEGCCqGSM49AwEHA0IABCkIHZ3mJCEPbIbUdh/Kz3zWW1C9wxnZOwfy
yrhr6aHwWREW3ZpMWKUcbsYup5kbouBc2dvMFUgoPBoaFYJ9D0SjaTBnMA4GA1Ud
DwEB/wQEAwIBpjAZBgNVHSUEEjAQBgRVHSUABggrBgEFBQcDATAPBgNVHRMBAf8E
BTADAQH/MCkGA1UdDgQiBCBIA/DmemwTGibbGe8uWjt5hnlE63SUsXuNKO9iGEhV
qDAKBggqhkjOPQQDAgNIADBFAiEAyoMO2BAQ3c9gBJOk1oSyXP70XRk4dTwXMF7q
R72ijLECIFKLANpgWFoMoo3W91uzJeUmnbJJt8Jlr00ByjurfAvv
-----END CERTIFICATE-----
可以通过 openssl 工具来查看其内容。
# openssl x509 -in example.com-cert.pem -noout -text
Certificate:
Data:
Version: 3 (0x2)
Serial Number:
22:13:22:47:3a:a4:0a:58:ea:dd:95:e7:b2:5e:84:8a
Signature Algorithm: ecdsa-with-SHA256
Issuer: C=US, ST=California, L=San Francisco, O=example.com, CN=example.com
Validity
Not Before: Apr 25 03:30:37 2017 GMT
Not After : Apr 23 03:30:37 2027 GMT
Subject: C=US, ST=California, L=San Francisco, O=example.com, CN=example.com
Subject Public Key Info:
Public Key Algorithm: id-ecPublicKey
Public-Key: (256 bit)
pub:
04:29:08:1d:9d:e6:24:21:0f:6c:86:d4:76:1f:ca:
cf:7c:d6:5b:50:bd:c3:19:d9:3b:07:f2:ca:b8:6b:
e9:a1:f0:59:11:16:dd:9a:4c:58:a5:1c:6e:c6:2e:
a7:99:1b:a2:e0:5c:d9:db:cc:15:48:28:3c:1a:1a:
15:82:7d:0f:44
ASN1 OID: prime256v1
X509v3 extensions:
X509v3 Key Usage: critical
Digital Signature, Key Encipherment, Certificate Sign, CRL Sign
X509v3 Extended Key Usage:
Any Extended Key Usage, TLS Web Server Authentication
X509v3 Basic Constraints: critical
CA:TRUE
X509v3 Subject Key Identifier:
48:03:F0:E6:7A:6C:13:1A:26:DB:19:EF:2E:5A:3B:79:86:79:44:EB:74:94:B1:7B:8D:28:EF:62:18:48:55:A8
Signature Algorithm: ecdsa-with-SHA256
30:45:02:21:00:ca:83:0e:d8:10:10:dd:cf:60:04:93:a4:d6:
84:b2:5c:fe:f4:5d:19:38:75:3c:17:30:5e:ea:47:bd:a2:8c:
b1:02:20:52:8b:00:da:60:58:5a:0c:a2:8d:d6:f7:5b:b3:25:
e5:26:9d:b2:49:b7:c2:65:af:4d:01:ca:3b:ab:7c:0b:ef
此外,还有 DER(Distinguished Encoding Rules)格式,是采用二进制对证书进行保存,可以与 PEM 格式互相转换。
证书信任链
证书中记录了大量信息,其中最重要的包括 签发的公开密钥 和 CA 数字签名 两个信息。因此,只要使用 CA 的公钥再次对这个证书进行签名比对,就能证明所记录的公钥是否合法。
读者可能会想到,怎么证明用来验证对实体证书进行签名的 CA 公钥自身是否合法呢?毕竟在获取 CA 公钥的过程中,它也可能被篡改掉。
实际上,CA 的公钥是否合法,一方面可以通过更上层的 CA 颁发的证书来进行认证;另一方面某些根 CA(Root CA)可以通过预先分发证书来实现信任基础。例如,主流操作系统和浏览器里面,往往会提前预置一些权威 CA 的证书(通过自身的私钥签名,系统承认这些是合法的证书)。之后所有基于这些 CA 认证过的中间层 CA(Intermediate CA)和后继 CA 都会被验证合法。这样就从预先信任的根证书,经过中间层证书,到最底下的实体证书,构成一条完整的证书信任链。
某些时候用户在使用浏览器访问某些网站时,可能会被提示是否信任对方的证书。这说明该网站证书无法被当前系统中的证书信任链进行验证,需要进行额外检查。另外,当信任链上任一证书不可靠时,则依赖它的所有后继证书都将失去保障。
可见,证书作为公钥信任的基础,对其生命周期进行安全管理十分关键。后面章节将介绍的 PKI 体系提供了一套完整的证书管理的框架,包括生成、颁发、撤销过程等。
PKI 体系
按照 X.509 规范,公钥可以通过证书机制来进行保护,但证书的生成、分发、撤销等步骤并未涉及。
实际上,要实现安全地管理、分发证书需要遵循 PKI(Public Key Infrastructure)体系。该体系解决了证书生命周期相关的认证和管理问题。
需要注意,PKI 是建立在公私钥基础上实现安全可靠传递消息和身份确认的一个通用框架,并不代表某个特定的密码学技术和流程。实现了 PKI 规范的平台可以安全可靠地管理网络中用户的密钥和证书。目前包括多个具体实现和规范,知名的有 RSA 公司的 PKCS(Public Key Cryptography Standards)标准和 OpenSSL 等开源工具。
PKI 基本组件
一般情况下,PKI 至少包括如下核心组件:
- CA(Certification Authority):负责证书的颁发和吊销(Revoke),接收来自 RA 的请求,是最核心的部分;
- RA(Registration Authority):对用户身份进行验证,校验数据合法性,负责登记,审核过了就发给 CA;
- 证书数据库:存放证书,多采用 X.500 系列标准格式。可以配合LDAP 目录服务管理用户信息。
其中,CA 是最核心的组件,主要完成对证书信息的维护。
常见的操作流程为,用户通过 RA 登记申请证书,提供身份和认证信息等;CA 审核后完成证书的制造,颁发给用户。用户如果需要撤销证书则需要再次向 CA 发出申请。
证书的签发
CA 对用户签发证书实际上是对某个用户公钥,使用 CA 的私钥对其进行签名。这样任何人都可以用 CA 的公钥对该证书进行合法性验证。验证成功则认可该证书中所提供的用户公钥内容,实现用户公钥的安全分发。
用户证书的签发可以有两种方式。可以由用户自己生成公钥和私钥,然后 CA 来对公钥内容进行签名(只有用户持有私钥);也可以由 CA 直接来生成证书(内含公钥)和对应的私钥发给用户(用户和 CA 均持有私钥)。
前者情况下,用户一般会首先自行生成一个私钥和证书申请文件(Certificate Signing Request,即 csr 文件),该文件中包括了用户对应的公钥和一些基本信息,如通用名(common name,即 cn)、组织信息、地理位置等。CA 只需要对证书请求文件进行签名,生成证书文件,颁发给用户即可。整个过程中,用户可以保持私钥信息的私密性,不会被其他方获知(包括 CA 方)。
生成证书申请文件的过程并不复杂,用户可以很容易地使用开源软件 openssl 来生成 csr 文件和对应的私钥文件。
例如,安装 openssl 后可以执行如下命令来生成私钥和对应的证书请求文件:
$ openssl req -new -keyout private.key -out for_request.csr
Generating a 1024 bit RSA private key
...........................++++++
............................................++++++
writing new private key to 'private.key'
Enter PEM pass phrase:
Verifying - Enter PEM pass phrase:
-----
You are about to be asked to enter information that will be incorporated
into your certificate request.
What you are about to enter is what is called a Distinguished Name or a DN.
There are quite a few fields but you can leave some blank
For some fields there will be a default value,
If you enter '.', the field will be left blank.
-----
Country Name (2 letter code) [AU]:CN
State or Province Name (full name) [Some-State]:Beijing
Locality Name (eg, city) []:Beijing
Organization Name (eg, company) [Internet Widgits Pty Ltd]:Blockchain
Organizational Unit Name (eg, section) []:Dev
Common Name (e.g. server FQDN or YOUR name) []:example.com
Email Address []:
Please enter the following 'extra' attributes
to be sent with your certificate request
A challenge password []:
An optional company name []:
生成过程中需要输入地理位置、组织、通用名等信息。生成的私钥和 csr 文件默认以 PEM 格式存储,内容为 base64 编码。
如生成的 csr 文件内容可能为:
$ cat for_request.csr
-----BEGIN CERTIFICATE REQUEST-----
MIIBrzCCARgCAQAwbzELMAkGA1UEBhMCQ04xEDAOBgNVBAgTB0JlaWppbmcxEDAO
BgNVBAcTB0JlaWppbmcxEzARBgNVBAoTCkJsb2NrY2hhaW4xDDAKBgNVBAsTA0Rl
djEZMBcGA1UEAxMQeWVhc3kuZ2l0aHViLmNvbTCBnzANBgkqhkiG9w0BAQEFAAOB
jQAwgYkCgYEA8fzVl7MJpFOuKRH+BWqJY0RPTQK4LB7fEgQFTIotO264ZlVJVbk8
Yfl42F7dh/8SgHqmGjPGZgDb3hhIJLoxSOI0vJweU9v6HiOVrFWE7BZEvhvEtP5k
lXXEzOewLvhLMNQpG0kBwdIh2EcwmlZKcTSITJmdulEvoZXr/DHXnyUCAwEAAaAA
MA0GCSqGSIb3DQEBBQUAA4GBAOtQDyJmfP64anQtRuEZPZji/7G2+y3LbqWLQIcj
IpZbexWJvORlyg+iEbIGno3Jcia7lKLih26lr04W/7DHn19J6Kb/CeXrjDHhKGLO
I7s4LuE+2YFSemzBVr4t/g24w9ZB4vKjN9X9i5hc6c6uQ45rNlQ8UK5nAByQ/TWD
OxyG
-----END CERTIFICATE REQUEST-----
openssl 工具提供了查看 PEM 格式文件明文的功能,如使用如下命令可以查看生成的 csr 文件的明文:
$ openssl req -in for_request.csr -noout -text
Certificate Request:
Data:
Version: 0 (0x0)
Subject: C=CN, ST=Beijing, L=Beijing, O=Blockchain, OU=Dev, CN=yeasy.github.com
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
RSA Public Key: (1024 bit)
Modulus (1024 bit):
00:f1:fc:d5:97:b3:09:a4:53:ae:29:11:fe:05:6a:
89:63:44:4f:4d:02:b8:2c:1e:df:12:04:05:4c:8a:
2d:3b:6e:b8:66:55:49:55:b9:3c:61:f9:78:d8:5e:
dd:87:ff:12:80:7a:a6:1a:33:c6:66:00:db:de:18:
48:24:ba:31:48:e2:34:bc:9c:1e:53:db:fa:1e:23:
95:ac:55:84:ec:16:44:be:1b:c4:b4:fe:64:95:75:
c4:cc:e7:b0:2e:f8:4b:30:d4:29:1b:49:01:c1:d2:
21:d8:47:30:9a:56:4a:71:34:88:4c:99:9d:ba:51:
2f:a1:95:eb:fc:31:d7:9f:25
Exponent: 65537 (0x10001)
Attributes:
a0:00
Signature Algorithm: sha1WithRSAEncryption
eb:50:0f:22:66:7c:fe:b8:6a:74:2d:46:e1:19:3d:98:e2:ff:
b1:b6:fb:2d:cb:6e:a5:8b:40:87:23:22:96:5b:7b:15:89:bc:
e4:65:ca:0f:a2:11:b2:06:9e:8d:c9:72:26:bb:94:a2:e2:87:
6e:a5:af:4e:16:ff:b0:c7:9f:5f:49:e8:a6:ff:09:e5:eb:8c:
31:e1:28:62:ce:23:bb:38:2e:e1:3e:d9:81:52:7a:6c:c1:56:
be:2d:fe:0d:b8:c3:d6:41:e2:f2:a3:37:d5:fd:8b:98:5c:e9:
ce:ae:43:8e:6b:36:54:3c:50:ae:67:00:1c:90:fd:35:83:3b:
1c:86
需要注意,用户自行生成私钥情况下,私钥文件一旦丢失,CA 方由于不持有私钥信息,无法进行恢复,意味着通过该证书中公钥加密的内容将无法被解密。
证书的吊销
证书超出有效期后会作废,用户也可以主动向 CA 申请吊销某证书文件。
由于 CA 无法强制收回已经颁发出去的数字证书,因此为了实现证书的作废,往往还需要维护一个吊销证书列表(Certificate Revocation List,CRL),用于记录已经吊销的证书序号。
因此,通常情况下,当对某个证书进行验证时,需要首先检查该证书是否已经记录在列表中。如果存在,则该证书无法通过验证。如果不在,则继续进行后续的证书验证过程。
为了方便同步吊销列表信息,IETF 提出了在线证书状态协议(Online Certificate Status Protocol,或 OCSP),支持该协议的服务可以实时在线查询吊销的证书列表信息。
Merkle 树结构
默克尔树(又叫哈希树)是一种典型的二叉树结构,由一个根节点、一组中间节点和一组叶节点组成。默克尔树最早由 Merkle Ralf 在 1980 年提出,曾广泛用于文件系统和 P2P 系统中。
其主要特点为:
- 最下面的叶节点包含存储数据或其哈希值。
- 非叶子节点(包括中间节点和根节点)都是它的两个孩子节点内容的哈希值。
进一步地,默克尔树可以推广到多叉树的情形,此时非叶子节点的内容为它所有的孩子节点的内容的哈希值。
默克尔树逐层记录哈希值的特点,让它具有了一些独特的性质。例如,底层数据的任何变动,都会传递到其父节点,一层层沿着路径一直到树根。这意味树根的值实际上代表了对底层所有数据的“数字摘要”。
目前,默克尔树的典型应用场景包括如下几种。
证明某个集合中存在或不存在某个元素
通过构建集合的默克尔树,并提供该元素各级兄弟节点中的 Hash 值,可以不暴露集合完整内容而证明某元素存在。
另外,对于可以进行排序的集合,可以将不存在元素的位置用空值代替,以此构建稀疏默克尔树(Sparse Merkle Tree)。该结构可以证明某个集合中不包括指定元素。
快速比较大量数据
对每组数据排序后构建默克尔树结构。当两个默克尔树根相同时,则意味着所代表的两组数据必然相同。否则,必然不同。
由于 Hash 计算的过程可以十分快速,预处理可以在短时间内完成。利用默克尔树结构能带来巨大的比较性能优势。
快速定位修改
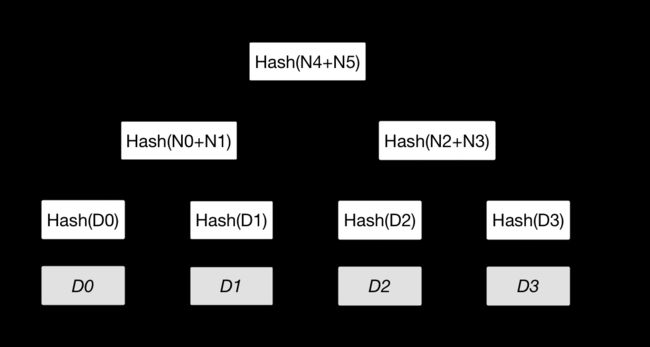
以下图为例,基于数据 D0……D3 构造默克尔树,如果 D1 中数据被修改,会影响到 N1,N4 和 Root。
图 1.8.7.1 - Merkle 树示例
因此,一旦发现某个节点如 Root 的数值发生变化,沿着 Root --> N4 --> N1,最多通过 O(lgN) 时间即可快速定位到实际发生改变的数据块 D1。
零知识证明
仍以上图为例,如何向他人证明拥有某个数据 D0 而不暴露其它信息。挑战者提供随机数据 D1,D2 和 D3,或由证明人生成(需要加入特定信息避免被人复用证明过程)。
证明人构造如图所示的默克尔树,公布 N1,N5,Root。验证者自行计算 Root 值,验证是否跟提供值一致,即可很容易检测 D0 存在。整个过程中验证者无法获知与 D0 相关的额外信息。
Bloom Filter 结构
布隆过滤器(Bloom Filter),1970 年由 Burton Howard Bloom 在论文《Space/Time Trade-offs in Hash Coding with Allowable Errors》提出。布隆过滤器是一种基于 Hash 的高效查找结构,能够快速(常数时间内)回答“某个元素是否在一个集合内”的问题。
该结构因为其高效性,被大量应用到网络和安全领域,例如信息检索(BigTable 和 HBase)、垃圾邮件规则、注册管理等。
基于 Hash 的快速查找
在布隆过滤器之前,先来看基于 Hash 的快速查找算法。在前面的讲解中,我们提到,Hash 可以将任意内容映射到一个固定长度的字符串,而且不同内容映射到相同串的概率很低。因此,这就构成了一个很好的“内容 -> 索引”的生成关系。
试想,如果给定一个内容和存储数组,通过构造 Hash 函数,让映射后的 Hash 值总不超过数组的大小,则可以实现快速的基于内容的查找。例如,内容 “hello world” 的 Hash 值如果是 “100”,则存放到数组的第 100 个单元上去。如果需要快速查找任意内容,如 “hello world” 字符串是否在存储系统中,只需要将其在常数时间内计算 Hash 值,并用 Hash 值查看系统中对应元素即可。该系统“完美地”实现了常数时间内的查找。
然而,令人遗憾的是,当映射后的值限制在一定范围(如总数组的大小)内时,会发现 Hash 冲突的概率会变高,而且范围越小,冲突概率越大。很多时候,存储系统的大小又不能无限扩展,这就造成算法效率的下降。为了提高空间利用率,后来人们基于 Hash 算法的思想设计出了布隆过滤器结构。
更高效的布隆过滤器
图 1.8.8.1 - 布隆过滤器
布隆过滤器采用了多个 Hash 函数来提高空间利用率。
对同一个给定输入来说,多个 Hash 函数计算出多个地址,分别在位串的这些地址上标记为 1。进行查找时,进行同样的计算过程,并查看对应元素,如果都为 1,则说明较大概率是存在该输入。
布隆过滤器相对单个 Hash 算法查找,大大提高了空间利用率,可以使用较少的空间来表示较大集合的存在关系。
实际上,无论是 Hash,还是布隆过滤器,基本思想是一致的,都是基于内容的编址。Hash 函数存在冲突,布隆过滤器也存在冲突。这就造成了两种方法都存在着误报(False Positive)的情况,但绝对不会漏报(False Negative)。
布隆过滤器在应用中误报率往往很低,例如,在使用 7 个不同 Hash 函数的情况下,记录 100 万个数据,采用 2 MB 大小的位串,整体的误判率将低于 1%。而传统的 Hash 查找算法的误报率将接近 10%。
同态加密
定义
同态加密(Homomorphic Encryption)是一种特殊的加密方法,允许对密文进行处理得到仍然是加密的结果。即对密文直接进行处理,跟对明文进行处理后再对处理结果加密,得到的结果相同。从抽象代数的角度讲,保持了同态性。
同态加密可以保证实现处理者无法访问到数据自身的信息。
如果定义一个运算符 ![]() ,对加密算法
,对加密算法 E 和 解密算法 D,满足:
![]()
则意味着对于该运算满足同态性。
同态性来自代数领域,一般包括四种类型:加法同态、乘法同态、减法同态和除法同态。同时满足加法同态和乘法同态,则意味着是代数同态,即全同态(Full Homomorphic)。同时满足四种同态性,则被称为算数同态。
对于计算机操作来讲,实现了全同态意味着对于所有处理都可以实现同态性。只能实现部分特定操作的同态性,被称为特定同态(Somewhat Homomorphic)。
问题与挑战
同态加密的问题最早在 1978 年由 Ron Rivest、Leonard Adleman 和 Michael L. Dertouzos 提出(同年 Ron Rivest、Adi Shamir 和 Leonard Adleman 还共同发明了 RSA 算法)。但第一个“全同态”的算法直到 2009 年才被克雷格·金特里(Craig Gentry)在论文《Fully Homomorphic Encryption Using Ideal Lattices》中提出并进行数学证明。
仅满足加法同态的算法包括 Paillier 和 Benaloh 算法;仅满足乘法同态的算法包括 RSA 和 ElGamal 算法。
同态加密在云计算和大数据的时代意义十分重大。目前,虽然云计算带来了包括低成本、高性能和便捷性等优势,但从安全角度讲,用户还不敢将敏感信息直接放到第三方云上进行处理。如果有了比较实用的同态加密技术,则大家就可以放心的使用各种云服务了,同时各种数据分析过程也不会泄露用户隐私。加密后的数据在第三方服务处理后得到加密后的结果,这个结果只有用户自身可以进行解密,整个过程第三方平台无法获知任何有效的数据信息。
另一方面,对于区块链技术,同态加密也是很好的互补。使用同态加密技术,运行在区块链上的智能合约可以处理密文,而无法获知真实数据,极大的提高了隐私安全性。
目前全同态的加密方案主要包括如下三种类型:
- 基于理想格(ideal lattice)的方案:Gentry 和 Halevi 在 2011 年提出的基于理想格的方案可以实现 72 bit 的安全强度,对应的公钥大小约为 2.3 GB,同时刷新密文的处理时间需要几十分钟。
- 基于整数上近似 GCD 问题的方案:Dijk 等人在 2010 年提出的方案(及后续方案)采用了更简化的概念模型,可以降低公钥大小至几十 MB 量级。
- 基于带扰动学习(Learning With Errors,LWE)问题的方案:Brakerski 和 Vaikuntanathan 等在 2011 年左右提出了相关方案;Lopez-Alt A 等在 2012 年设计出多密钥全同态加密方案,接近实时多方安全计算的需求。
目前,已知的同态加密技术往往需要较高的计算时间或存储成本,相比传统加密算法的性能和强度还有差距,但该领域关注度一直很高,笔者相信,在不远的将来会出现接近实用的方案。
函数加密
与同态加密相关的一个问题是函数加密。
同态加密保护的是数据本身,而函数加密顾名思义保护的是处理函数本身,即让第三方看不到处理过程的前提下,对数据进行处理。
该问题已被证明不存在对多个通用函数的任意多密钥的方案,目前仅能做到对某个特定函数的一个密钥的方案。
其它技术
密码学领域涉及到的技术还有许多,这里总结一些还在发展和探讨中的话题。
零知识证明
零知识证明(Zero Knowledge Proof),是这样的一个过程,证明者在不向验证者提供任何额外信息的前提下,使验证者相信某个论断(Statement)是正确的。
证明过程包括交互式(Interactive)和非交互式(Non-interactive)两种。
零知识证明的研究始于 Shafi Goldwasser,Silvio Micali 和 Charles Rackoff 在 1985 年提交的开创性论文《The Knowledge Complexity of Interactive Proof-Systems》,三位作者也因此在 1993 年获得首届哥德尔奖。
论文中提出了零知识证明要满足三个条件:
- 完整性(Completeness):真实的证明可以让验证者成功验证;
- 可靠性(Soundness):虚假的证明无法保证通过验证。但理论上可以存在小概率例外;
- 零知识(Zero-Knowledge):如果得到证明,无法(或很难)从证明过程中获知除了所证明信息之外的任何信息,分为完美零知识、概率零知识。
交互式零知识证明相对容易构造,需要通过证明人和验证人之间一系列交互完成。一般为验证人提出一系列问题,证明人如果能都回答正确,则有较大概率确实知道论断。
例如,证明人 Alice 向验证人 Bob 证明两个看起来一样的图片有差异,并且自己能识别这个差异。Bob 将两个图片在 Alice 无法看到的情况下更换或保持顺序,再次让 Alice 识别是否顺序调整。如果 Alice 每次都能正确识别顺序是否变化,则 Bob 会以较大概率认可 Alice 的证明。此过程中,Bob 除了知道 Alice 确实能识别差异这个论断外,自己无法获知或推理出任何额外信息(包括该差异本身),也无法用 Alice 的证明(例如证明过程的录像)去向别人证明。注意这个过程中 Alice 如果提前猜测出 Bob 的更换顺序,则存在作假的可能性。
非交互式零知识证明(NIZK)则复杂的多。实际上,通用的非交互式完美或概率零知识证明(Proof)系统并不存在,但可以设计出计算安全的非交互式零知识论证(Argument)系统,具有广泛的应用价值。
Manuel Blum、Alfredo De Santis、Silvio Micali 和 Giuseppe Persiano 在 1991 年发表的论文《Noninteractive Zero-Knowledge》中提出了首个面向“二次非连续问题”的非交互的完美零知识证明(NIPZK)系统。
2012 年,Nir Bitansky、Ran Caneetti 等在论文《From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again》中提出了实用的非交互零知识论证方案 zk-SNARKs,后来在 Z-cash 等项目中得到广泛应用。目前,进行非交互式零知识论证的主要思路为利用所证明论断创造一个难题(一般为 NP 完全问题如 SAT,某些情况下需要提前或第三方提供随机数作为参数)。如果证明人确实知道论断,即可在一定时间内解决该难题,否则很难解答难题。验证人可以通过验证答案来验证证明人是否知晓论断。
零知识证明如果要能普及,还需要接受实践检验,另外需要考虑减少甚至无需预备阶段计算、提高可扩展性,同时考虑抵御量子计算攻击。
可验证随机函数
可验证随机函数(Verifiable Random Function,VRF)最早由 Silvio Micali(麻省理工学院)、Michael Rabiny(哈佛大学)、Salil Vadha(麻省理工学院)于 1999 年在论文《Verifiable Random Functions》中提出。
它讨论的是一类特殊的伪随机函数,其结果可以在某些场景下进行验证。一般可以通过签名和哈希操作来构建。
例如,Alice 拥有公钥 Pk 和对应私钥 Sk。Alice 宣称某可验证随机函数 F 和一个输入 x,并计算 y = F(Sk, x)。Bob 可以使用 Alice 公钥 Pk,对同样的 x 和 F 进行验证,证明其结果确实为 y。注意该过程中,因为 F 的随机性,任何人都无法预测 y 的值。
可见,VRF 提供了一种让大家都认可并且可以验证的随机序列,可以用于分布式系统中进行投票的场景。
安全多方计算
安全多方计算(Secure Multi-Party Computation,SMPC 或 SMC)由 Andrew Chi-Chih Yao(姚期智)于 1986 年在论文《How to generate and exchange secrets》中提出。其假设的场景为多个参与方都拥有部分数据,在不泄露自己数据的前提下,实现利用多方的数据进行计算。这一问题在多方彼此互不信任而又需要进行某些合作时(如保护隐私的前提下进行数据协同),十分有用,有时候也被称为隐私保护计算(Privacy-preserving Computation)。
根据参与方的个数,可以分为双方计算或多方计算;根据实现方法,可以分为基于噪音(如 differential privacy,差分隐私)、基于秘密共享(Secret Sharing)、基于混淆电路(Garbled Circuit)和基于同态加密(Homomorphic Encryption)。
一般来说,基于噪音的方案容易实现,但使用场景局限,基于密码学技术的方案更通用,但往往需要较大计算成本。
不经意传输
不经意传输(Oblivious Transfer,OT)协议由 S. Even,O. Goldreich,A. Lempel 等人 1983 年在论文《A Randomized Protocol for Signing Contracts》中提出。后来应用在安全多方计算等场景下。
该协议所解决的问题是发送方将信息发送给接收方,但要保护双方的隐私:发送方无法获知接收方最终接收了哪些信息;接收方除了能获知自己所需的信息外,无法获得额外的信息。
例如,银行向征信公司查询某个客户的征信情况以决定是否进行贷款,银行不希望征信公司知道该客户来到该银行申请贷款(属于客户隐私),同时,征信公司不希望银行拿到其它客户的征信数据。
一种简单的实现是发送方发送 N 个公钥给接收方,接收方随机选择一个公钥加密一个对称密钥并将结果返回发送方。发送方分别用 N 个私钥进行解密,其中 1 个结果为对称密钥,N-1 个为随机串,但发送方无法区别。发送方用 N 个解密结果分别加密 1 条消息(共计 N 条)并返回给接收方。接收方只能解密其中 1 条消息。如果双方提前约定好 N 对结果进行盲化的随机串,接收方还可以挑选只接收某个特定信息。
另外一种简单实现是接收方提供 N 个随机串作为公钥,并证明自己只知道其中 K 个串对应的私钥。发送方采用这些随机串加密 N 个信息,然后发给接收方。这样,接收方只能解开其中的 K 条信息。
差分隐私
差分隐私(Differential Privacy)是一种相对实用的隐私保护机制。
最初问题是研究如何分享一个数据集而保护数据集中个体的隐私,在 2006 年由 Cynthia Dwork、Frank McSherry、 Kobbi Nissim 和 Adam Smith 在论文《Calibrating Noise to Sensitivity in Private Data Analysis》中提出。由于在隐私保护问题上的应用前景,近些年成为研究热点。
主要思想是在数据集中巧妙的添加一些噪音扰动,使得对修改后数据集进行计算不太影响统计结果,但无法将其中任意个体追溯回原始个体信息。例如,将数据集中删掉任意一条记录,查询结果不受影响。
目前可行的方案主要包括添加拉普拉斯噪音(适合于数值型)和指数噪音(适合于非数值型)等。
量子密码学
量子密码学(Quantum Cryptography)随着量子计算和量子通信的研究而被受到越来越多的关注,被认为会对已有的密码学安全机制产生较大的影响。
量子计算的概念最早是物理学家费曼于 1981 年提出,基本原理是利用量子比特可以同时处于多个相干叠加态,理论上可以同时用少量量子比特来表达大量的信息,并同时进行处理,大大提高计算速度。量子计算目前在某些特定领域已经展现出超越经典计算的潜力。如基于量子计算的 Shor 算法(1994 年提出),理论上可以实现远超经典计算速度的大数因子分解。2016 年 3 月,人类第一次以可扩展的方式,用 Shor 算法完成对数字 15 的质因数分解。
这意味着目前广泛应用的非对称加密算法,包括基于大整数分解的 RSA、基于椭圆曲线随机数的 ECC 等将来都将很容易被破解。当然,现代密码学体系并不会因为量子计算的出现而崩溃。一方面,量子计算设备离实际可用的通用计算机还有较大距离,密码学家可以探索更安全的密码算法。另一方面,很多安全机制尚未发现能加速破解的量子算法那,包括数字签名(基于 Hash)、格(Lattice)密码、基于编码的密码等。
量子通信则可以提供对密钥进行安全协商的机制,有望实现无条件安全的“一次性密码”。量子通信基于量子纠缠效应,两个发生纠缠的量子可以进行远距离的实时状态同步。一旦信道被窃听,则通信双方会获知该情况,丢弃此次传输的泄露信息。该性质十分适合进行大量的密钥分发,如 1984 年提出的 BB84 协议,结合量子通道和公开信道,可以实现安全的密钥分发。
注:一次性密码:最早由香农提出,实现理论上绝对安全的对称加密。其特点为密钥真随机且只使用一次;密钥长度跟明文一致,加密过程为两者进行二进制异或操作。
社交工程学
密码学与安全问题,一直是学术界和工业界都十分关心的重要话题,相关的技术也一直在不断发展和完善。然而,即便存在理论上完美的技术,也不存在完美的系统。无数例子证实,看起来设计十分完善的系统最后被攻破,并非是因为设计上出现了深层次的漏洞。而问题往往出在事后看来十分浅显的一些方面。
例如,系统管理员将登陆密码贴到电脑前;财务人员在电话里泄露用户的个人敏感信息;公司职员随意运行来自不明邮件的附件;不明人员借推销或调查问卷的名义进入办公场所窃取信息……
著名计算机黑客和安全顾问 Kevin David Mitnick 曾在 15 岁时成功入侵北美空中防务指挥系统,在其著作《The Art of Deception》中大量揭示了通过社交工程学的手段轻易获取各种安全信息的案例。
本章小结
本章主要总结了密码学与安全领域中的一些核心问题和经典算法。通过阅读本章内容,相信读者已经对现代密码学的发展状况和关键技术有了初步了解。掌握这些知识,对于理解区块链系统如何实现隐私保护和安全防护都很有好处。
现代密码学安全技术在设计上大量应用了十分专业的现代数学知识,如果读者希望能够深入学习其原理,则需要进一步学习并掌握近现代的数学科学,特别是数论、抽象代数等相关内容。
从应用的角度来看,完善的安全系统除了核心算法外,还需要包括协议、机制、系统、人员等多个方面。任何一个环节出现漏洞都将带来巨大的安全风险。因此,实践中要实现真正高安全可靠的系统是十分困难的。
区块链中大量利用了现代密码学的已有成果;反过来,区块链在诸多场景中的应用也提出了很多新的需求,促进了安全学科的进一步发展。