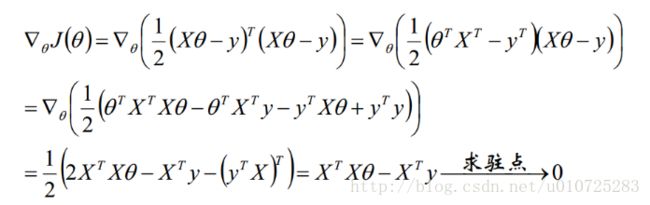一文搞懂深度学习正则化的L2范数
想要彻底弄明白L2范数,必须要有一定的矩阵论知识,L2范数涉及了很多的矩阵变换。在我们进行数学公式的推到之前,我们先对L2范数有一个感性的认识。
L2范数是什么?
L2范数的定义其实是一个数学概念,其定义如下:
这个公式看着相当熟悉吧,用的最多的欧式距离就是一种L2范数,表示向量元素的平方和再开方。
正则化中的L2范数
说到正则化,我们要看一下,正则化在深度学习中含义是指什么?正则化其实是一种策略,以增大训练误差为代价来减少测试误差的所有策略我们都可以称作为正则化。换句话说就是正则化是为了防止模型过拟合。L2范数就是最常用的正则化方法之一。
如何使用L2范数来正则化?
为了方便理解,就以线性规划模型来举个例子,线性规划模型的代价函数也就是平方误差之和,如下:
找到线性模型的解就是找到一个theta值能够使代价函数J取得最小值,也就是对J进行求导,之后得到导数为0的点,我们称为驻点。用数学的方式来看就是:、
这个过程是没有使用正则化的线性规划模型的求解过程,加上L2范数,其实很简单,就是在代价函数后加上theta的L2范数即可。
L2范数的使用就完成了,这样就能够防止模型过拟合了,使用优化算法时也有加快收敛的效果。
但是为什么呐?为什么加上一个参数的L2范数就可以达到这样神奇的效果呐?
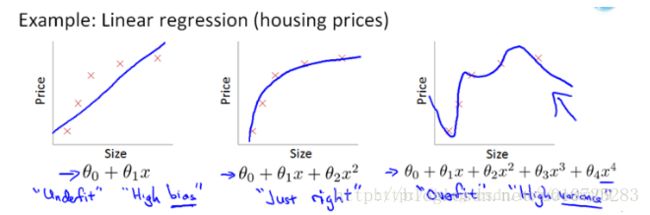
在一探究竟之前我们先看一下L2范数的另一个别名:权重衰减。这里的权重就是指我们要学习到的参数,衰减意思就很明白了,将一些权重进行了缩小,使其影响变小,这样就可以达到防止过拟合了。好像不是很明白,让我们张图,有个感性认识。
这张图是Ng课程中用来讲解什么是过拟合的,最右侧的那条曲线就是一个过拟合的模型,因为这个模型对数据太过敏感了,只要数据一丁点的变化,模型的输出就会有所变化,这肯定带来的后果就是泛化能力很差,在训练集上表现良好的模型,在测试集上表现却会变差。模型的输出对数据的输入过于敏感的程度用专业的数学来表达的话就是condition number,这里不重点讲解了。
用上图解释了什么是过拟合后,我们再看是什么带来了过拟合,好像中间的模型和右侧的模型只是差了theta3和theta4参数
而已,也就是我们如果能够抑制这两个参数的话,我们就可以防止模型过拟合了。对,这可不就是权重衰减吗?!只要我们更多
的抑制这两个参数而更小的抑制其他参数就可以完成正则化了。我们再来捋一下思路,
我们使用L2范数==》抑制模型中产生过拟合的参数==》防止了过拟合
最初其实还有个疑问就是,我们既然知道了多加参数会产生过拟合,那么最初设置参数的时候为什么不设置更少的参数?如果
设置合适的参数确实可以不用使用正则化的任何策略。或者如果知道数据的分布,就根本不用使用什么机器学习或者深度学习的
方法,我们直接设置参数就可以了对吧。设置多的参数就是因为我们对数据是未知的,我们不知道哪个参数会起作用?
那么思路到现在,我们只需要明白L2范数是怎么对模型中的参数进行抑制的就明白了L2范数到底是怎么回事了。
再看一下线性回归的代价函数:
加上L2正则项后的代价函数是:
加入L2正则项后的目标是:对中的某些项有所抑制。
以下就是正式的数学推导:
以上对L2范数对权重的衰减的理解很明白了,但是还是有些晦涩,我们再换另一种有趣的理解方法。
看上面这个公式,我们得到了正则化后的权重和原本之前权重之间的关系。又因为Q是正交基,所以我们可以看作左乘Q是对矩阵的一种旋转,左乘![]() 是对矩阵的拉伸,如果不是太明白可以看下图:
是对矩阵的拉伸,如果不是太明白可以看下图:
也就是说, 对权重进行了缩小,而且针对不同的权重进行不同比例的缩小。这就又要求我们理解特征值
对权重进行了缩小,而且针对不同的权重进行不同比例的缩小。这就又要求我们理解特征值![]() 的含义。
的含义。
再看下面这一段:
也就是说,![]() 是
是![]() 的特征值,也就是
的特征值,也就是![]() 的开方就是X的奇异值!,那么我们就有了X矩阵的奇异值分解,如果奇
的开方就是X的奇异值!,那么我们就有了X矩阵的奇异值分解,如果奇
异值不熟悉的可以移步:http://blog.csdn.net/u010725283/article/details/79155204 ,好的那么我们知道矩阵X的主要成分在前面的奇异值上,换句话说就是前面比较大的奇异值更能代表X,我们终于找到了![]() 的含义,
的含义,![]() 是从大到小的一个排序,越大的奇异值越能代表X,而我们的权重就是为了得到X的分布!那么
是从大到小的一个排序,越大的奇异值越能代表X,而我们的权重就是为了得到X的分布!那么![]() 的含义就是越大的越能代表数据的分布,对应的权重越重要,
的含义就是越大的越能代表数据的分布,对应的权重越重要, 中,
中,![]() 越大,对
越大,对![]() 的抑制越小,反过来也就是抑制越大。这一下就完全明白了,就是对于数据不够重要的权重抑制的大一些,对数据分布越起作用的权重抑制越小,这就实现了正则化,就能够防止过拟合了!
的抑制越小,反过来也就是抑制越大。这一下就完全明白了,就是对于数据不够重要的权重抑制的大一些,对数据分布越起作用的权重抑制越小,这就实现了正则化,就能够防止过拟合了!
L2范数简单却神奇!
参考文献:
SVD和PCA:http://blog.csdn.net/u010725283/article/details/79155204
如何理解矩阵特征值:https://www.zhihu.com/question/21874816
机器学习中的L0,L1,L2范数:http://blog.csdn.net/zouxy09/article/details/24971995
L2正则项解收缩的解释:https://zhuanlan.zhihu.com/p/27131373