数据结构与算法面试题总结
目录
1 树定义
1.1 二叉树
1.2 满二叉树
1.3 完全二叉树
1.4 平衡二叉树 / AVL树
1.5 二分搜索树
1.6 二叉堆
1.7 线段树
1.8 Trie字典树
1.9 红黑树
2 多叉树转成二叉树
3 AVL树的旋转操作
4 HashMap的底层结构
5 HashMap的put操作和get操作底层的实现原理
5.1 put
5.2 get
6 ConcurrentHashMap在Java 7和Java 8之中实现的区别
7 排序算法
7.1 选择排序
7.2 冒泡排序
7.3 插入排序
7.4 希尔排序
7.5 堆排序
7.6 归并排序
7.7 快速排序
7.8 时间复杂度
8 二分查找
9 二分搜索树遍历
9.1 前序遍历
9.2 中序遍历
9.3 后序遍历
9.4 层序遍历
10 链表反转
11 斐波那契数列
1 树定义
1.1 二叉树
- 二叉树具有唯一根节点
- 二叉树每个节点最多有两个孩子
- 二叉树每个节点最多有一个父亲
1.2 满二叉树
- 除了最后一层的叶子节点之外,其他层的所有节点都有两个孩子
1.3 完全二叉树
- 树中元素按一层一层,从左到右的顺序存放
- 完全二叉树不一定是满二叉树,但它不满的那部分一定是在整棵树的右下部
1.4 平衡二叉树 / AVL树
- 对于任意一个节点,左子树和右子树的高度差不能超过1
1.5 二分搜索树
- 二分搜索树的每个结点的值:
- 大于其左子树的所有节点的值
- 小于其右子树的所有节点的值
1.6 二叉堆
- 最大堆中某个节点的值总是不大于其父节点的值
- parent(i) = (i - 1) / 2
- left child(i) = 2 * i + 1
- right child(i) = 2 * i + 2
1.7 线段树
- 线段树中每个节点表示的是一个区间内的统计值
- 如果区间有n个元素, 线段树用数组表示需要4n的空间
1.8 Trie字典树
- 将整个字符串以字母为单位,一个一个拆开,从根节点开始到叶子节点去遍历。每遍历到一个叶子节点,就形成了一个单词
- 查询每个字符串的时间复杂度,和字典中一共有多少个字符串无关,只和该字符串的长度相关
1.9 红黑树
- 每个节点或者是红色的,或者是黑色的
- 根节点是黑色的
- 每一个NULL节点是黑色的
- 如果一个节点是红色的,那么它的孩子都是黑色的
- 从任意一个节点到叶子节点,经过的黑色节点数量是一样的
2 多叉树转成二叉树
- 将树中所有的兄弟节点之间连一条线。
- 对于树中的每一个节点,只保留其与第一个左孩子之间的连线,去掉其他孩子节点与该节点的连线。
- 以树中的根节点为轴心,将树按顺时针旋转一定的角度即可。
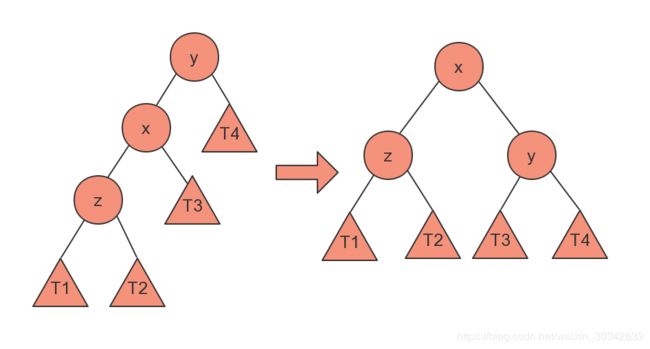
3 AVL树的旋转操作
以右旋转为例,其示意图如下:
伪代码如下:
x.right = y;
y.left = T3;4 HashMap的底层结构
Java 7:数组+链表
Java 8:数组+链表+红黑树
5 HashMap的put操作和get操作底层的实现原理
5.1 put
-
首先判断当前map是否为空,如果为空,则初始化。
-
然后根据hash & (length-1)找到数组下标位置,判断要插入的位置处是否有值,没值就放值。
-
有值的话:
-
首先判断第一个位置处的数据的key和hash是否和需要插入的值的key和hash相同,如果相同,则记录该位置。
-
否则判断是否是红黑树,如果是,则插入树节点,并返回新节点的位置。
-
否则就是链表的插入过程:遍历链表进行插入,如果当前节点数=7(需要转换成红黑树的阈值-1),则进行链表转化成红黑树的过程。在遍历中如果找到key和hash和要插入值的key和hash相同的节点是,记录当前的位置。
-
-
当记录的位置不为null,也就是属于上述三种情况之一的话,则进行值的覆盖。
-
最后size加一后判断当前是否需要扩容,如果是则扩容。
5.2 get
-
计算key的hash值,根据hash & (length-1)找到数组下标位置。
-
判断数组第一个节点的key和hash是否和要找值的key和hash相同,如果相同,则直接返回。
-
否则判断第一个节点是否是红黑树,如果是,则执行红黑树的查找工作。
-
否则的话就遍历链表,直到找到key和hash和要找值的key和hash都相同的节点。
6 ConcurrentHashMap在Java 7和Java 8之中实现的区别
《1》:
Java 7:分段锁+数组+链表
Java 8:CAS+synchroized+数组+链表+红黑树
《2》:
在扩容操作中Java 8中是多线程操作,每个线程每次负责迁移其中的一部分,每个线程每做完一个任务再检测是否有其他没做完的任务,有就帮助迁移。
《3》:
Java 7是头插节点,Java 8是尾插节点。
7 排序算法
以下算法都是以从小到大的顺序为例。
7.1 选择排序
每次循环都会找出当前循环中最小的元素,然后和此次循环中的队首元素进行交换。
public int[] selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i; j < array.length; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
if (minIndex > i) {
int temp = array[i];
array[i] = array[minIndex];
array[minIndex] = temp;
}
}
return array;
}7.2 冒泡排序
每次循环都比较前后两个元素的大小,如果前者大于后者,则将两者进行交换。这样做会将每次循环中最大的元素替换到末尾,逐渐形成有序集合。将每次循环中的最大元素逐渐由队首转移到队尾的过程形似“冒泡”过程,故因此得名。
public int[] bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
for (int j = 0; j < array.length - 1 - i; j++) {
if (array[j] > array[j + 1]) {
int temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}
return array;
}7.3 插入排序
插入排序的精髓在于每次都会在先前排好序的子集合中插入下一个待排序的元素,每次都会判断待排序元素的上一个元素是否大于待排序元素,如果大于,则将元素右移,判断再上一个元素与待排序元素;否则该处就应该是该元素的插入位置。
public int[] insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i - 1;
while (j >= 0 && array[j] > temp) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = temp;
}
return array;
}7.4 希尔排序
希尔排序其实就是分组排序。其关键思想是采用了一个增量increment的概念。每次会不断比较该元素和该元素加上increment后的位置处的大小。从广义上讲,也就是说将源数组拆分成几个小数组进行内部排序。increment会不断减小,拆分的粒度也会越来越细,最后increment会减小到为1,此时该排序会退化成冒泡排序,这次排序完成后即为最终结果。
比如说现有{1,3,5,2,4}这一个数组,假设increment一开始为2:
- 那么首先会将1(0)和5(0+2)进行比较(括号内为索引值,括号前为实际值),1小于5满足条件,然后将5(2)和4(2+2)进行比较,5大于4,则将两者进行交换,此时该数组为{1,3,4,2,5},这一次比较过程完成。
- 此时将指针重新指向第二个元素3(1),继续判断3(1)和2(1+2),3大于2,将两者交换,此时该数组为{1,2,4,3,5},这一次比较过程完成。
- 此时将指针重新指向第三个元素4(2),继续判断4(2)和5(2+2),4小于5,数组不动,此时该数组依然为{1,2,4,3,5},这一次比较过程完成。
- 此时第一次大的比较过程全部完成,将increment减半,变为1,再从第一个元素开始比较。注意此时会将每一个元素和之后的下一个元素进行比较,如上面所说,此时会变成冒泡排序。这一次排序过后的结果为{1,2,3,4,5}。当increment为1时排序过后的结果即为最终结果。
理论上来说,随着increment的不断变小,分组粒度会越来越细,比较和交换的性能也会越来越低,increment减到1时达到最低点。但因为此时数组已经经过了多次的分组排序,该数组已经是一个类似排序好的数组,所以最后一次排序性能也不会下降太多。广而言之,最后几次的排序过程相比前几次的排序,时间消耗不会相差太多。这便是希尔排序的优势所在。
同时在下面的例子中,increment一开始取值为数组的数量除以2,当然也可以有别的取法,比如length/3+1、取奇数、取质数等等。
public int[] shellSort(int[] array) {
int increment = array.length >>> 1;
while (increment >= 1) {
for (int i = 0; i < array.length; i++) {
for (int j = i; j < array.length - increment; j = j + increment) {
if (array[j] > array[j + increment]) {
int temp = array[j];
array[j] = array[j + increment];
array[j + increment] = temp;
}
}
}
increment >>>= 1;
}
return array;
}7.5 堆排序
堆排序的过程是首先构建一个大顶堆,大顶堆首先是一棵完全二叉树,其次它保证堆中某个节点的值总是不大于其父节点的值。
因为大顶堆中的最大元素肯定是根节点,所以每次取出根节点即为当前大顶堆中的最大元素,取出后再重新构建大顶堆,再取出根节点,再重新构建…重复这个过程,直到数据都被取出,最后取出的结果即为排好序的结果。
public class MaxHeapForSort {
/**
* 排序数组
*/
private int[] nodeArray;
/**
* 数组的真实大小
*/
private int size;
private int parent(int index) {
return (index - 1) >>> 1;
}
private int leftChild(int index) {
return (index << 1) + 1;
}
private int rightChild(int index) {
return (index << 1) + 2;
}
private void swap(int i, int j) {
int temp = nodeArray[i];
nodeArray[i] = nodeArray[j];
nodeArray[j] = temp;
}
private void siftUp(int index) {
//如果k处节点的值大于其父节点的值,则交换两个节点值,同时将k指向其父节点,继续向上循环判断
while (index > 0 && nodeArray[index] > nodeArray[parent(index)]) {
swap(index, parent(index));
index = parent(index);
}
}
private void siftDown(int index) {
//左孩子的索引比size小,意味着索引k处的节点有左孩子,证明此时k节点不是叶子节点
while (leftChild(index) < size) {
//maxIndex记录的是k节点左右孩子中最大值的索引
int maxIndex = leftChild(index);
//右孩子的索引小于size意味着k节点含有右孩子
if (rightChild(index) < size && nodeArray[rightChild(index)] > nodeArray[maxIndex]) {
maxIndex = rightChild(index);
}
//如果k节点值比左右孩子值都大,则终止循环
if (nodeArray[index] >= nodeArray[maxIndex]) {
break;
}
//否则进行交换,将k指向其交换的左孩子或右孩子,继续向下循环,直到叶子节点
swap(index, maxIndex);
index = maxIndex;
}
}
private void add(int value) {
nodeArray[size] = value;
size++;
//构建大顶堆
siftUp(size - 1);
}
private void extractMax() {
//将堆顶元素和最后一个元素进行交换
swap(0, size - 1);
//此时并没有删除元素,而只是将size-1,剩下的元素重新构建成大顶堆
size--;
//重新构建大顶堆
siftDown(0);
}
public int[] heapSort(int[] array) {
nodeArray = new int[array.length];
for (int i = 0; i < array.length; i++) {
add(array[i]);
}
for (int i = 0; i < array.length; i++) {
extractMax();
}
return nodeArray;
}
}
7.6 归并排序
归并排序使用的是分治的思想,首先将数组不断拆分,直到最后拆分成两个元素的子数组,将这两个元素进行排序合并,再向上递归。不断重复这个拆分和合并的递归过程,最后得到的就是排好序的结果。
合并的过程是将两个指针指向两个子数组的首位元素,两个元素进行比较,较小的插入到一个temp数组中,同时将该数组的指针右移一位,继续比较该数组的第二个元素和另一个元素…重复这个过程。最后temp数组保存的便是这两个子数组排好序的结果。最后将temp数组复制回原数组的位置处即可。
public int[] mergeSort(int[] array) {
return mergeSort(array, 0, array.length - 1);
}
private int[] mergeSort(int[] array, int left, int right) {
if (left < right) {
int mid = left + ((right - left) >>> 1);
// 拆分子数组
mergeSort(array, left, mid);
mergeSort(array, mid + 1, right);
// 对子数组进行合并
merge(array, left, mid, right);
}
return array;
}
private void merge(int[] array, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
// p1和p2为需要对比的两个数组的指针,k为存放temp数组的指针
int p1 = left, p2 = mid + 1, k = 0;
while (p1 <= mid && p2 <= right) {
if (array[p1] <= array[p2]) {
temp[k++] = array[p1++];
} else {
temp[k++] = array[p2++];
}
}
// 把剩余的数组直接放到temp数组中
while (p1 <= mid) {
temp[k++] = array[p1++];
}
while (p2 <= right) {
temp[k++] = array[p2++];
}
// 复制回原数组
for (int i = 0; i < temp.length; i++) {
array[i + left] = temp[i];
}
}7.7 快速排序
快速排序的核心是要有一个基准数据temp,一般取数组的第一个位置元素。然后需要有两个指针left和right,分别指向数组的第一个和最后一个元素。
首先从right开始,比较right位置元素和基准数据。如果大于等于,则将right指针左移,比较下一位元素;否则将right指针处数据赋给left指针处(此时left指针处数据已保存进temp中),left指针+1,之后开始比较left指针处数据。
拿left位置元素和基准数据进行比较。如果小于等于,则将left指针右移,比较下一位元素;否则将left指针处数据赋给right指针处,right指针-1,之后开始比较right指针处数据…重复这个过程。
直到left和right指针相等时,说明这一次比较过程完成。此时将先前存放进temp中的基准数据赋值给当前left和right指针共同指向的位置处,即可完成这一次排序操作。
之后递归排序基础数据的左半部分和右半部分,递归的过程和上面讲述的过程是一样的,只不过数组范围不再是原来的全部数组了,而是现在的左半部分或右半部分。当全部的递归过程结束后,最终结果即为排好序的结果。
public int[] quickSort(int[] array) {
return quickSort(array, 0, array.length - 1);
}
private int[] quickSort(int[] array, int start, int end) {
// left和right指针分别指向array的第一个和最后一个元素
int left = start, right = end;
// temp存放的是array中的start位置的元素,也就是需要比较的基准数据
int temp = array[start];
while (left < right) {
// 首先从right指针开始比较,如果right指针位置处数据大于temp,则将right指针左移
while (left < right && array[right] >= temp) {
right--;
}
// 如果找到一个right指针位置处数据小于temp,则将right指针处数据赋给left指针处
if (left < right) {
array[left] = array[right];
left++;
}
// 然后从left指针开始比较,如果left指针位置处数据小于temp,则将left指针右移
while (left < right && array[left] <= temp) {
left++;
}
// 如果找到一个left指针位置处数据大于temp,则将left指针处数据赋给right指针处
if (left < right) {
array[right] = array[left];
right--;
}
}
// 当left和right指针相等时,此时循环跳出,将之前存放的基准数据赋给当前两个指针共同指向的数据处
array[left] = temp;
// 一次替换后,递归交换基准数据左边的数据
if (start < left - 1) {
array = quickSort(array, start, left - 1);
}
// 之后递归交换基准数据右边的数据
if (right + 1 < end) {
array = quickSort(array, right + 1, end);
}
return array;
}7.8 时间复杂度
| 排序算法 | 时间复杂度 | ||
| 平均情况 | 最好情况 | 最坏情况 | |
| 选择排序 | |||
| 冒泡排序 | |||
| 插入排序 | |||
| 希尔排序 | |||
| 堆排序 | |||
| 归并排序 | |||
| 快速排序 | |||
8 二分查找
public int binarySearch(int[] array, int target) {
return binarySearch(array, 0, array.length - 1, target);
}
private int binarySearch(int[] array, int left, int right, int target) {
if (left >= right) {
return -1;
}
int mid = left + ((right - left) >>> 1);
if (array[mid] == target) {
return mid;
} else if (array[mid] < target) {
return binarySearch(array, mid + 1, right, target);
} else {
return binarySearch(array, left, mid, target);
}
}9 二分搜索树遍历
9.1 前序遍历
public void preOrder() {
preOrder(root);
}
private void preOrder(Node cur) {
if (cur == null) {
return;
}
System.out.print(cur.value + " ");
preOrder(cur.left);
preOrder(cur.right);
}9.2 中序遍历
public void inOrder() {
inOrder(root);
}
private void inOrder(Node cur) {
if (cur == null) {
return;
}
inOrder(cur.left);
System.out.print(cur.value + " ");
inOrder(cur.right);
}9.3 后序遍历
public void postOrder() {
postOrder(root);
}
private void postOrder(Node cur) {
if (cur == null) {
return;
}
postOrder(cur.left);
postOrder(cur.right);
System.out.print(cur.value + " ");
}9.4 层序遍历
public void levelOrder() {
if (root == null) {
return;
}
Queue q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
Node cur = q.remove();
System.out.print(cur.value + " ");
if (cur.left != null) {
q.add(cur.left);
}
if (cur.right != null) {
q.add(cur.right);
}
}
} 10 链表反转
import java.util.Random;
public class MyLinkedList {
private class Node {
private int value;
private Node next;
private Node(int value, Node next) {
this.value = value;
this.next = next;
}
@Override
public String toString() {
return Integer.toString(value);
}
}
private Node head;
private void addFirst(int value) {
head = new Node(value, head);
}
public void reverse() {
reverse(head);
}
private Node reverse(Node cur) {
if (cur == null || cur.next == null) {
head = cur;
return cur;
}
Node nextNode = reverse(cur.next);
nextNode.next = cur;
cur.next = null;
return cur;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
for (Node cur = head; cur != null; cur = cur.next) {
res.append(cur + "->");
}
res.append("NULL");
return res.toString();
}
public static void main(String[] args) {
MyLinkedList list = new MyLinkedList();
Random r = new Random();
for (int i = 0; i < 10; i++) {
list.addFirst(r.nextInt(100));
}
System.out.println(list);
list.reverse();
System.out.println(list);
}
}11 斐波那契数列
public int fibonacci(int index) {
if (index == 1 || index == 2) {
return 1;
} else {
return fibonacci(index - 1) + fibonacci(index - 2);
}
}