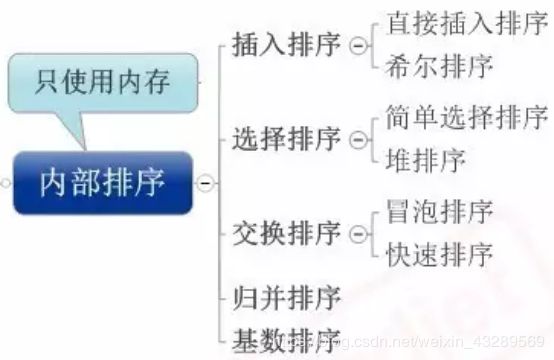
Java--常见排序算法
import java.util.Arrays;
public class Bubble {
public static void main(String[] args) {
int []a={23,4,56,2,7,18,9};
for(int i=0;i<a.length;i++){
for(int j=0;j<a.length-1-i;j++){
int t;
if(a[j]>a[j+1]){
t=a[j];
a[j]=a[j+1];
a[j+1]=t;
}
}
}
System.out.println(Arrays.toString(a));
}
}
冒泡排序通过一趟又一趟地比较数组中的每一个元素,使较大的数据下沉,较小的数据上升。是最慢的、效率最低的算法。
冒泡排序平均时间复杂度为O(n^2),是稳定的算法。
二、插入排序
import java.util.Arrays;
//从1号下标开始
//越有序越快,最好情况O(n)
public class Insert {
public static void main(String[] args) {
int[] a = {23, 4, 56, 2, 7, 18, 9};
for(int i=1;i<a.length;i++){
for(int j=0;j<=i;j++){
if(a[j]>a[i]){
int t=a[j];
a[j]=a[i];
a[i]=t;
}
}
System.out.println(Arrays.toString(a));
}
System.out.println();
System.out.println(Arrays.toString(a));
}
}
插入排序通过把序列中的值插入一个已经排序好的序列中,直到该序列的结束,可看作是对冒泡排序的改进。
插入排序平均时间复杂度为O(n^2),是稳定的算法。
三、选择排序
import java.util.Arrays;
public class Select {
public static void main(String[] args) {
int[] a = {23, 4, 56, 2, 7, 18, 9};
for (int i = 0; i < a.length - 1; i++) {
int index = i;
for (int j = i + 1; j < a.length; j++) {
if (a[j] < a[index]) {
index = j;// 保存最小元素的下标
}
}
// 此时已经找到最小元素的下标
// 将最小元素与前面的元素交换
int t = a[index];
a[index] = a[i];
a[i] = t;
}
System.out.println(Arrays.toString(a));
}
}
在实际应用中处于和冒泡排序基本相同的地位,使用较少。
选择排序平均时间复杂度为O(n^2),是不稳定的算法。
四、希尔排序
import java.util.Arrays;
public class Shell {
public static void main(String[] args) {
int[] arr = {23, 4, 56, 2, 7, 18, 9};
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
for (int i = gap; i < arr.length; i++) {
for (int j = i - gap; j >= 0; j -= gap) {
if (arr[j] > arr[j + gap]) {
int t = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = t;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
}
解决了插入排序只能相邻项之间交换的问题,通过将数据分成不同的组,先对每一组进行排序,然后再对所有的元素进行一次插入排序,以减少数据交换和移动的次数。适合操作数据量较小的数列重复排序。分组的合理性会对算法产生重要的影响。一般选择奇数分组避免出现重复分组的情况。
希尔排序平均时间复杂度为O(nlog(n)),是不稳定的算法。
五、快速排序
import java.util.Arrays;
public class QuickSort {
public static int part(int[] arr, int left, int right) {
int start = arr[left];
while (left < right) {
while (arr[right] >= start && right > left) right--;
arr[left] = arr[right];
while (arr[left] <= start && right > left) left++;
arr[right] = arr[left];
}
arr[left] = start;
return left;
}
public static void quickSort(int[] arr, int left, int right) {
if (left < right) {
int i = part(arr, left, right);
quickSort(arr, left, i - 1);
quickSort(arr, i + 1, right);
}
}
public static void main(String[] args) {
int arr[] = {23, 4, 56, 2, 7, 18, 9};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
}
通过一趟排序将待排序列分成独立的两部分,选取基准,创建两个移动的变量,一个从右向左移动,一个从左向右移动,以此遍历左右两边的元素,并将大于基准的放在右边,小于基准的放在左边,当两个移动的变量重合时,遍历结束,整个排序过程可以递归进行。时间复杂度为O(n^2),是不稳定的排序。