深度学习的基础知识(RNN、LSTM等模型、梯度消失与爆炸、正则化、优化方式)

今天在看迁移学习中的一个模型COVE，里面用到了LSTM（ELMo也是），故而想回顾一下深度学习中的一些基础知识。

一、网络结构

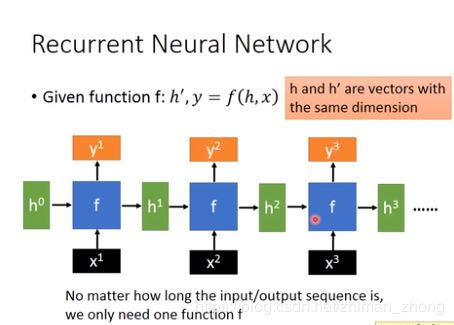
1.RNN

在此之前先介绍fully connected、CNN、RNN等重要architecture（参见台大李宏毅老师的教程）

 

RNN与传统的feedward的区别在于：允许信息的持久化，即基于原始的信息去处理新的信息。

 

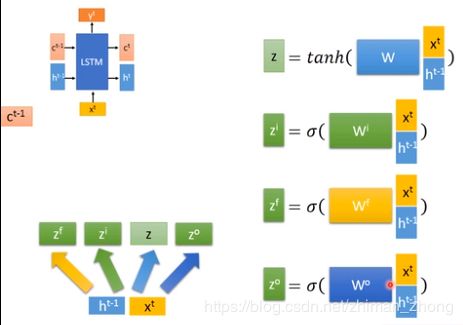
2.LSTM

但RNN不能处理长期依赖的问题（长期依赖指输出的根据离输出时刻太远，譬如根据当前视频段预测接下来视频，如果当前视频只与先前不久的视频相关，那么RNN可以很好的解决这个问题。但如果当前视频依赖于很久之前的视频，比如电影的结尾与开头相呼应，那么RNN就会表现很差）

Long Short Term Memory（LSTM）是一种 RNN 特殊的类型，可以很好解决这个问题。LSTM是在标准的RNN的基础上加入了其他的神经网络（gates），而这些gates只是控制数级，控制信息的流动量。

下面就是LSTM的计算过程。

 

 

二、优化方法

1.过拟合（面经当中问的较多）

      正则化是指在经验风险上加一个正则项或罚项，正则项一共有两种L1正则化和L2正则化，或者L1范数和L2范数。

（1）L1正则化：可使参数稀疏，排除无关特征的干扰，稀疏化的结果使优化后的参数一部分为0

（2）L2正则化：可使参数平滑，防止过拟合（让L2范数的正则项||W||2最小，可以使得W的每个元素都很小，并且更加平均。而越小的参数说明模型越简单，越简单的模型越不容易产生过拟合的现象）

注：防止过拟合还可以采取

（3）早停策略：将数据集划分成训练集和验证集，训练集用来计算梯度，更新权值，验证集用来估计误差，若训练集误差降低但验证集误差升高，则停止训练。

（4）dropout（随机失活）：通过在反向传播误差更新权值时候随机选择一部分权值不更新，相当于随机删除一部分hidden units（不是真实删除了，只是暂时不使用这部分units），由于是随机丢弃，故而每一个mini-batch都在训练不同的网络，有点类似集成学习的思想。dropout强迫一个神经单元，和随机挑选出来的其他神经单元共同工作，达到好的效果，减弱了神经元节点间的联合适应性，增强了泛化能力，通过这样的方法能防止过拟合。

 

2.梯度爆炸与梯度消失

（1）产生原因

因为sigmoid的导函数最大值为0.25（在x特别小或者特别大时导数接近于0），在链式求导与反向传播中：

• 梯度消失：如果初始化权重较小，W<1，当神经网络特别深的时候，则多个W和小于0.25（甚至接近于0）的值连乘起来，梯度呈指数级衰减。当梯度趋于0 ，权重和偏差参数无法被更新，导致神经网络无法被优化。
• 梯度爆炸：如果初始化权重较大，W>10，当神经网络特别深的时候，则多个W和小于0.25（甚至接近于0）的值连乘起来，梯度呈指数级增长
• 解决方法：好的参数初始化方式（如He初始化），非饱和的激活函数（如 ReLU），批量规范化、LSTM

反向传播原理：可以说是梯度下降在链式法则中的应用

从输入信号前传到输出，计算输出层误差，再将误差根据链式求导逐层向前传播，得到连接权和阈值的更新公式

（2）梯度爆炸解决办法

A.梯度剪切

设置一个梯度剪切阈值，更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内。

B.权重正则化

比较常见的是l1/l2正则,如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。

 

（3）梯度消失解决方法(更常见）

A.激励函数ReLU

激励函数用ReLU而不用sigmoid，优点主要在于：1.计算快（线性函数） 2.避免梯度消失（sigmoid和tanh的gradient在饱和区域x很大或者很小时，导数接近于0，很容易造成梯度消失的问题，几乎更新不了，减缓收敛速度），而RELU的正数部分导数为1

缺点：由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）

 

B.Batch Norm

（1）产生原因：机器学习理论依赖于样本独立同分布假设，而神经网络中，各层输入值在训练过程中其分布逐渐发生偏移或者变动，整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因

（2）思想：BN就是通过一定的规范化手段（减去均值除以方差），把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化

（3）优点：让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

 

C.残差网络

残差可以很轻松的构建几百层，一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分，其中残差单元如下图所示：

在上图的残差网络结构图中，通过“shortcut connections（捷径连接）”的方式，直接把输入x传到输出作为初始结果，输出结果为H(x)=F(x)+x，当F(x)=0时，那么H(x)=x，也就是上面所提到的恒等映射。于是，深度残差网络将学习目标改变了，学习的是目标值H(X)和x的差值，也就是所谓的残差。因此，后面的训练目标就是要将残差结果逼近于0，使到随着网络加深，准确率不下降。
这种残差跳跃式的结构，打破了传统的神经网络n-1层的输出只能给n层作为输入的惯例，使某一层的输出可以直接跨过几层作为后面某一层的输入，其意义在于为叠加多层网络而使得整个学习模型的错误率不降反升的难题提供了新的方向。

 

D.LSTM结构：复杂的门结构导致不易发生梯度消失

 

3.梯度下降优化方式

详细SGD、momentum、Adagrad、RMSprop、Adam讲解如此篇博客

batch GD：每轮迭代都需要在整个数据集上计算一次,非常慢

SGD：每轮迭代都随机选一个样本，容易陷入局部最优

Mini-batch GD：每次从所有训练数据中取一个子集用于计算梯度，计算较快，收敛较为稳定

momentum：GD方法的一个缺点是其更新方向完全依赖于当前batch计算出的梯度，因而十分不稳定；Momentum算法会观察历史梯度，若当前梯度的方向与历史梯度一致（表明当前样本不太可能为异常点），则会增强这个方向的梯度，若当前梯度与历史梯方向不一致，则梯度会衰减。

Adagrad：自适应学习率，学习率除以之前所有梯度值平方和的开方值，整体的学习率会越来越小

RMSprop：自适应学习率，学习率除以之前所有梯度值的平均值

Adam：Momentum与RMSprop的结合