COCI2016/2017 Round1T4 Mag
文章目录
- 题目
- 分析
- 代码
题目
分析
既然是乘积,容易想到所选路径上的值不可能很大,所以一般(特殊情况等会讨论)有以下几个结论:
- 最优路径上不可能有点权超过 2 2 2的结点
证明:
设当前已找到的乘积为 x x x,结点个数为 n n n,新加入的点权为 y ( y > 2 ) y(y>2) y(y>2),则新的路权为 x y n + 1 \dfrac{xy}{n+1} n+1xy,由于 y > 2 y>2 y>2,所以一定有 x y n + 1 > x n \dfrac{xy}{n+1}>\dfrac{x}{n} n+1xy>nx,故新路径不可能更优。
- 最优路径上不可能有超过 1 1 1个点权为 2 2 2的点
证明:
设路径上有 k ( k > 1 ) k(k>1) k(k>1)个权为 2 2 2的结点, n − k ( n ≥ k ) n-k(n\geq k) n−k(n≥k)个权为 1 1 1的结点,则路权为 2 k n \dfrac{2^k}{n} n2k,易得 2 k n ≥ 2 k − 1 n − 1 \dfrac{2^k}{n}\geq\dfrac{2^{k-1}}{n-1} n2k≥n−12k−1(当且仅当 n = k = 2 n=k=2 n=k=2时取等号)。
所以,我们只需要找这样的链:只由点权为 1 1 1的点构成,或只由一个点权为 2 2 2的点和若干点权为 1 1 1的点构成。
问题就变成了以下两个步骤:
- 找到树上的连续的 1 1 1链
- 得到最长的一个连续的 1 1 1链,得到一个可能的答案 1 n \dfrac{1}{n} n1( n n n为这个链的长度)
- 找到数 2 2 2,看它能否链接两个 1 1 1链,若能,找到最长的两个,用这个 2 2 2把它们连起来,得到一个可能的答案 2 x + y + 1 \dfrac{2}{x+y+1} x+y+12( x x x, y y y为这两个 1 1 1链的长度)
- 找到最小答案,约分输出
改题的时候我自己写了调了一晚上没弄出来,最后照着std打才理解了这道题实现的奇妙。
无根树的树形DP真的恶心。
设根为结点 1 1 1,
定义dpDown和dpUp两个数组,dpDown[u]表示以 u u u的儿子 v v v为起点,在 u u u的子树的最长的连续 1 1 1的长度;dpUp[u]表示以 u u u的父亲为起点,不在 u u u子树的最长的连续 1 1 1的长度。
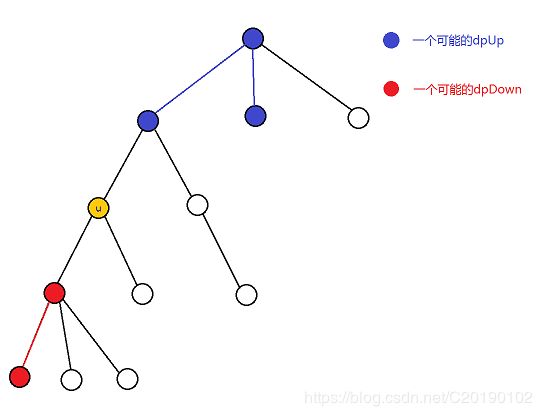
dpDown的转移很简单: d p D o w n [ u ] = max v ∈ c h i l d r e n [ u ] { d p D o w n [ v ] + 1 X v = 1 0 X v ≠ 1 dpDown[u]=\max\limits_{v\in children[u]} \begin{cases} dpDown[v]+1& &X_v=1\\ 0& &X_v\neq 1\\ \end{cases} dpDown[u]=v∈children[u]max{dpDown[v]+10Xv=1Xv̸=1
重点是dpUp:
发现它可以分成两种情况:
- 直接转移为
dpUp[fa[u]],即不考虑 u u u的兄弟子树,上图表示的就是一种这样的情况 - 考虑 u u u的兄弟子树,那么就是 u u u的父亲与 u u u的某个兄弟相连,如下图的绿色部分
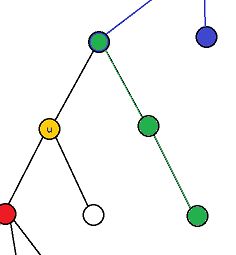
所以: d p U p [ u ] = max { d p U p [ f a [ u ] ] , { 0 X f a [ u ] ≠ 1 max v ∈ c h i l d r e n [ f a [ u ] ] v ≠ u d p D o w n [ v ] + 1 X f a [ u ] = 1 } dpUp[u]=\max\left\{dpUp[fa[u]], \begin{cases} 0& &X_{fa[u]}\neq 1\\ \max\limits_{v\in children[fa[u]]}^{v\neq u}dpDown[v]+1& &X_{fa[u]}=1 \end{cases} \right\} dpUp[u]=max⎩⎨⎧dpUp[fa[u]],⎩⎨⎧0v∈children[fa[u]]maxv̸=udpDown[v]+1Xfa[u]̸=1Xfa[u]=1⎭⎬⎫
乍一看是 n 2 n^2 n2的,然而里面那个max显然可以用两个数组优化成 O ( 1 ) O(1) O(1):
LeftMax[u]表示先根序中 u u u之前的 u u u的兄弟 b b b 里最大的那个dp[b]RightMax[u]表示先根序中 u u u之后的 u u u的兄弟 b b b 里最大的那个dp[b]
所以: max v ∈ c h i l d r e n [ f a [ u ] ] v ≠ u d p [ v ] = max { L e f t M a x [ u ] , R i g h t M a x [ u ] } \max\limits_{v\in children[fa[u]]}^{v\neq u}dp[v]=\max\{LeftMax[u],RightMax[u]\} v∈children[fa[u]]maxv̸=udp[v]=max{LeftMax[u],RightMax[u]}
于是给的那 20 % 20\% 20%的 n ≤ 1000 n\leq 1000 n≤1000的点就是考虑的最后一步??
这个部分分真的迷,,,
得到了这两个数组就好办了, u u u如果要连接两个链,有两种情况:
- 一条在 u u u子树,另一条在 u u u头上
- 两条都在 u u u子树
当然还有一点特殊情况:没有一个点的权值为 1 1 1,那就输出权值最小点的权值就好(可以在DP里面处理掉)。
代码
#include
