深度学习: Non-Maximum Supression (非极大值抑制)

NMS (Non-Maximum Supression)

NMS来 选取那些邻域里分数最高的窗口，同时抑制那些分数低的窗口 。

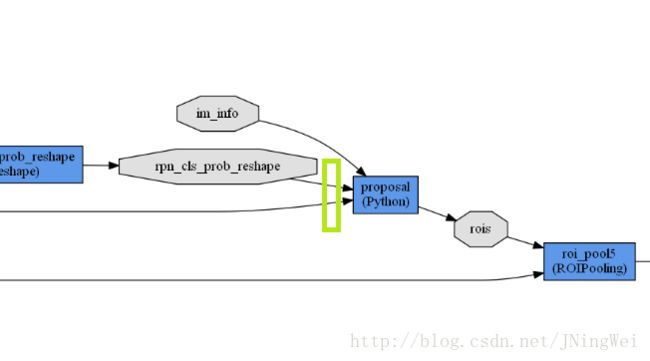
由 论文可见，在 Faster R-CNN 中，NMS算法被放在RPN网络的末段，用于 协助 剔除低得分的box：

Note:

• 所有NMS算法都是在每个类内分别独立进行NMS。

• NMS算法略显粗暴，直接将和得分最大的box的IOU大于某个阈值的box的 得分置零 或者 丢弃box 。后续的改良版——Soft NMS，改用稍低一点的分数 ( score*(1-iou) ) 来代替原有的分数，而不是直接置零。

在 Faster R-CNN 中位于下图中的 绿框位置：

Test

我经过动手实验，成功复现了 NMS 的处理过程。

未经过NMS之前的bbox分布：

经过NMS筛选后的保留的bbox分布：

Code

效果图所对应的源码如下：

# coding=utf-8

import numpy as np
import cv2


def nms(bboxs, thresh):

    x1, y1, x2, y2, scores = list([bboxs[:, i] for i in range(len(bboxs[0]))])
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)    # 每块 bbox 面积

    order = scores.argsort()[::-1]    # 所有 bbox 根据置信度 进行 index排序
    keep = []    # 筛选后 要留下来的 bbox
    while order.size > 0:
        i = order[0]    # 置信度最高的bbox 的 index
        keep.append(i)    # 先 留下 剩下的bbox 中 置信度最高的bbox 的index

        # 选择大于x1,y1和小于x2,y2的区域
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])
        # 当前bbox 与 每个剩余的 bbox 分别的 重叠区域
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h    # [ 12272.  11716.  13566.      0.      0.]    [ 8181.]

        # 交叉区域面积 / (bbox + 某区域面积 - 交叉区域面积)
        overlap = inter / (areas[i] + areas[order[1:]] - inter)    # [ 0.73362028  0.62279396  0.52134814  0.          0.        ]   [ 0.61832061]

        # 保留交集小于一定阈值的boundingbox
        idxs = np.where(overlap <= thresh)[0]    # [3 4]    []

        order = order[idxs + 1]    # [0 3]    []

    return keep


def draw_bbox(bboxs, pic_name):
    pic = np.zeros((850, 850), np.uint8)
    for bbox in bboxs:
        x1, y1, x2, y2 = map(int, bbox[:-1])
        pic = cv2.rectangle(pic, (x1, y1), (x2, y2), (255, 0, 0), 2)
    cv2.imwrite('./{}.jpg'.format(pic_name), pic)


if __name__ == "__main__":
    bboxs = np.array([
        [720, 690, 820, 800, 0.5],
        [204, 102, 358, 250, 0.5],
        [257, 118, 380, 250, 0.8],
        [700, 700, 800, 800, 0.4],
        [280, 135, 400, 250, 0.7],
        [255, 118, 360, 235, 0.7]])
    thresh = 0.3
    draw_bbox(bboxs, "Before_NMS")
    keep = nms(bboxs, thresh)    # [2, 0]
    draw_bbox(bboxs[keep], "After_NMS")

算法缺陷

NMS算法的 核心思想 是：在 假设 实例之间均为不重叠或低重叠的 前提 下，去除高重叠bbox。

该核心思想也导致了NMS不可避免地会对 高重叠的实例 产生 漏检 。