·计算机视觉」立体视觉 对极几何 (Epipolar Geometry) 本质矩阵E 基础矩阵F
致敬 (参考书)永远的丰碑 必看的书
计算机视觉中的多视图几何
学习opencv (参考书)
联想：地球-南北极 对极几何
本质矩阵(本征矩阵) 相机坐标系的关系
基础矩阵 图像像素坐标系的关系（加入内参）
先思考一个问题：用两个相机在不同的位置拍摄同一物体，如果两张照片中的景物有重叠的部分，我们有理由相信，这两张照片之间存在一定的对应关系，本节的任务就是如何描述它们之间的对应关系，描述工具是对极几何 ，它是研究立体视觉的重要数学方法。
要寻找两幅图像之间的对应关系，最直接的方法就是逐点匹配，如果加以一定的约束条件对极约束(epipolar constraint)，搜索的范围可以大大减小。
先回顾简单的立体成像系统
对极约束的图示
更一般的立体成像关系：两个相机的坐标无任何约束关系，相机的内部参数可能不同，甚至是未知的。要刻画这种情况下的两幅图像之间的对应关系，需要引入两个重要的概念——对极矩阵(Epipolar Matrix)和基本矩阵(Fundamental Matrix)。
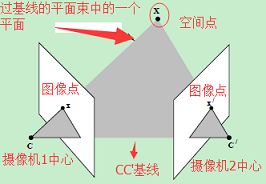
对极几何中的重要概念（参考下图）：
极点：极点:右相机坐标原点在左像平面上的像；极点:左相机坐标原点在右像平面上的像
极平面：由两个相机坐标原点、和物点P组成的平面
级线：极平面与两个像平面的交线，即和
级线约束：两极线上点的对应关系
对极几何图，通过上面几幅图示，利用对极几何的约束关系，我们可以：
1. 找到物点P在左像平面上的像点；
2. 画出极线；
3. 找到极平面与右像平面的交线，即得极线；
4. 像点的对应点一定在极一上。
两个相机坐标系之间的关系为
由于R是正交矩阵，因此可写为
三向量共面，它们的混合积为零(混合积对应于有向体积)
将向量乘(叉乘)写成矩阵的形式
通过进一步的改写，可以得到左像点和右像点之间约束关系(非常简单、漂亮)
显然，左像点和右像点是通过矩阵来约束的，我们称矩阵为本质矩阵(Essential Matrix)，它的基本性质有：
• has rank 2(秩为2)
• depends only on the EXTRINSIC Parameters (R & T)(仅依赖于外部参数R和T)
本质矩阵(本征矩阵) 相机坐标系的关系
https://www.cnblogs.com/houkai/p/6661607.html
两个相机坐标系的关系：
是物体P在
相机坐标系的位置,
是物体P在
坐标系的位置。相对于的旋转矩阵为R,位移为T。则：
由于R是正交矩阵，可以写成：
由于三向量共面，如下图，所以它们的混合积为0.
将叉乘写成矩阵相乘的形式：
令：
，S是一个秩为2的矩阵，则：
显然，
和
可以通过矩阵E=RS来约束，我们称E为本质约束(Essential Matrix)。它具有两个性质：
- 秩为2
- 只依赖于外部参数R和T
基础矩阵 图像像素坐标系的关系（加入内参）
继续前面的本质矩阵，结合成像的集合关系：
这里的
和
是在单位距离坐标系下的位置.如果我们要分析的是图像，需要转到像素坐标系下，此时：
从而有：
我们称矩阵F为基础矩阵：
，性质是：
- 秩为2
- 依赖于相机内参和外部参数R和T
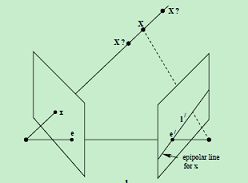
基础矩阵给出了：在已知一个点和F的情况下，其匹配点的直线约束方程：
直线约束方程为：
进一步分析：
而这里的F是秩为2的矩阵，所以存在：
和
。
e表示它满足所有的直线约束，也就是上面图中那一堆直线的交点，物理意义便是cam2(cam1)在cam1(cam2)的像平面的投影，即极点。
使用SVD分解即可求得极点。
一. 对极几何基本概念
对极几何（Epipolar Geometry）描述的是两幅视图之间的内在射影关系，与外部场景无关，只依赖于摄像机内参数和这两幅试图之间的的相对姿态。
1. 基线（baseline）：直线CC'为基线。
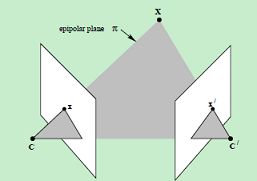
2. 对极平面束（epipolar pencil）：以基线为轴的平面束。
3. 对极平面（epipolar plane）：任何包含基线的平面都称为对极平面。
4. 对极点（epipole）：摄像机的基线与每幅图像的交点。比如，上图中的点e和e'。
5. 对极线（epipolar line）：对极平面与图像的交线。比如，上图中的直线l和l'。
6. 5点共面：点x，x'，摄像机中心C、C'，空间点X是5点共面的。
7. 极线约束：两极线上点的对应关系。
说明：直线l是对应于点x'的极线，直线l'是对应于点x的极线。极线约束是指点x'一定在对应于x的极线l'上，点x一定在对应于x'的极线l上。
二. 对极几何原理
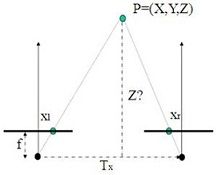
1. 理想模型
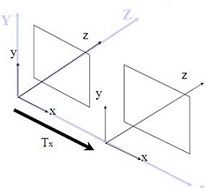
假设两个相机的内部参数一致，比如焦距、镜头等，为了数学描述的方便，需引入坐标，由于坐标是人为引入的，因此客观世界中的事物可以处于不同的坐标系中。假设两个相机的X轴方向一致，像平面重叠，坐标系以左相机为准，右相机相对于左相机是简单的平移，用坐标表示为(Tx,0,0)。如下所示：
在左右相机中像平面像点的坐标，如下所示：
综上可知，深度Z和视差d成反比，这也是为什么近的物体看起来比远的物体移动的快。
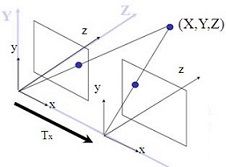
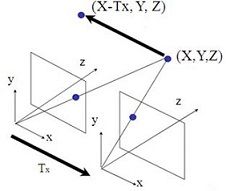
2. 实际模型
更一般的立体成像关系是两个相机的坐标无任何约束关系，相机的内部参数可能不同，甚至是未知的。要刻画这种情
况下的两幅图像之间的对应关系，需要引入两个重要的概念：本征矩阵E和基本矩阵F。本征矩阵E包含物理空间中两个摄像机相关的旋转和平移信息，基础矩阵F除了包含E的信息外，还包含两个摄像机的内参数。本征矩阵E将左摄像机观测到的点的物理坐标与右摄像机观测到的相同点的位置关联起来。基础矩阵F则是将一台摄像机的像平面上的点在图像坐标（像素）上的坐标和另一台摄像机的像平面上的点关联起来。
（1）本质矩阵E
本质矩阵E的推导过程，如下所示：
，
（R是正交矩阵），，，
，，，，，，
左像平面上的一点乘以本质矩阵E，结果为一条直线，该直线就是的对极线，且过在右像平面上的对应点。本质矩阵E的基本性质：秩为2，且仅依赖于外部参数R和T。其中，P表示物点矢量，p表示像点矢量。
（2）基础矩阵
由于本质矩阵E并不包含相机内参信息，且E是面向相机坐标系的。实际上，我们更感兴趣的是在像素坐标系上去研究一个像素点在另一视图上的对极线，这就需要用到相机内参信息将相机坐标系和像素坐标系联系起来。假设和是物理坐标值，其对应的像素坐标值为和，相机内参矩阵为M，那么。根据，那么。令基础矩阵，那么。
三. OpenCV双目相机标定实现 [7]] OpenCV双目相机标定：http://blog.csdn.net/t247555529/article/details/48046859
参考文献：
[1] 对极几何基本概念：http://blog.csdn.net/tina_ttl/article/details/52749542
[2] 计算机视觉基础-视差与深度信息：http://www.360doc.com/content/14/0205/03/10724725_349968116.shtml
[3] 计算机视觉基础-对极几何：http://www.360doc.com/content/14/0205/02/10724725_349963695.shtml
[4] 计算机视觉基础-本质矩阵和基本矩阵：http://www.360doc.com/content/14/0205/03/10724725_349965748.shtml
[5] 本质矩阵和基础矩阵的区别是什么：https://www.zhihu.com/question/27581884
[6] 对极几何--本质矩阵E和基础矩阵F：http://blog.csdn.net/tanmengwen/article/details/7409886