Tensorflow学习笔记：基础篇（2）——多项式回归

Tensorflow学习笔记：基础篇（2）——多项式回归

---

— 前文学习笔记（1）中说到线性回归并不能很好的拟合正弦的问题，loss函数值不甚理想，本文将在上文的Tensorflow程序中进行修改，框架结构不变，数据集也不变，仅把线性回归修改为多项式回归，看看最终效果如何~~
—废话少说，直接进入正题

---

计算流程

1、数据准备

2、准备好placeholder

3、初始化参数/权重

4、计算预测结果

5、计算损失值

6、初始化optimizer

7、指定迭代次数，并在session执行graph

---

代码示例

1、数据准备

与上文相同未做修改，在【-3，3】内生成100个点，使用正弦函数上加上了随机噪声

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

n_observations = 100
xs = np.linspace(-3, 3, n_observations)
ys = np.sin(xs) + np.random.uniform(-0.5, 0.5, n_observations)
plt.scatter(xs, ys)
plt.show()

2、准备好placeholder

X = tf.placeholder(tf.float32, name='X')
Y = tf.placeholder(tf.float32, name='Y')

3、初始化参数/权重

多项式回归问题，此处使用 y = w3 x^3 + w2 x^2 + w1 x + b进行拟合，此处构造四个变量 w1、w2、w3 与 b，比前文多了两个高次项权重

W = tf.Variable(tf.random_normal([1]), name='weight')
B = tf.Variable(tf.random_normal([1]), name='bias')
W_2 = tf.Variable(tf.random_normal([1]), name='weight_2')
W_3 = tf.Variable(tf.random_normal([1]), name='weight_3')

4、计算预测结果

y = w3 x^3 + w2 x^2 + w1 x + b
其中tf.pow()函数即为指数运算，例如：tf.pow(X, 2) 表示为x的2次方

Y_pred = tf.add(tf.multiply(X, W), B)
Y_pred = tf.add(tf.multiply(tf.pow(X, 2), W_2), Y_pred)
Y_pred = tf.add(tf.multiply(tf.pow(X, 3), W_3), Y_pred)

5、计算损失值

此次损失函数，我使用均值平方根，当然你也可以选用其他统计量作为损失函数值的评价方法

loss = tf.reduce_sum(tf.pow(Y_pred - Y, 2)) / sample_num

6、初始化optimizer

梯度下降函数保持不变，使得loss函数的值取到极小值

learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)

7、指定迭代次数，并在session执行graph

init = tf.global_variables_initializer()
sess.run(init)

再次强调！！！此处两句极其重要，需要先初始化变量，才能进行读取和写入（赋值）操作

n_sample = xs.shape[0]
init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)

        for i in range(1000):
        total_loss = 0
        for x, y in zip(xs, ys):
            __, l = sess.run([optimizer, loss], feed_dict={X: x, Y: y})
            total_loss += l
        if i % 20 == 0:
            print('Epoch{0}:{1}'.format(i, total_loss/n_sample))

    W, W_2, W_3, B = sess.run([W, W_2, W_3, B])

plt.scatter(xs, ys)
plt.plot(xs, xs**3*W_3 + xs**2*W_2 + xs*W + B)
plt.show()

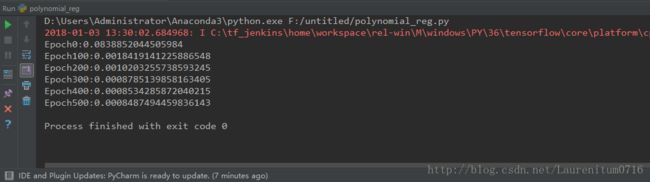
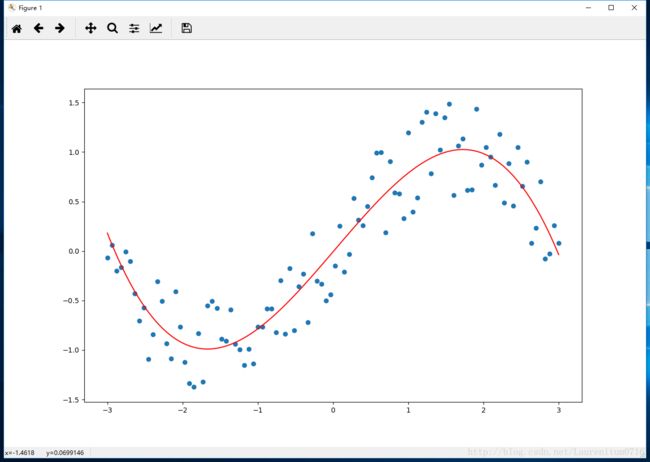
运行结果

迭代计算500次，可以发现loss值较前文的线性回归已经有了明显改善，这是因为用多项式拟合正弦函数，可以理解为正弦函数的泰勒级数展开，如果感兴趣可以尝试将多项式最高次数继续提高，再比较loss函数值的变化。
大家是不是已经大概熟悉这个框架了呢，其实就是一个套路~~~

---

完整代码

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt


#数据准备
n_observations = 100
xs = np.linspace(-3, 3, n_observations)
ys = np.sin(xs) + np.random.uniform(-0.5, 0.5, n_observations)
#plt.scatter(xs, ys)
#plt.show()


#准备好placeholder
X = tf.placeholder(tf.float32, name='X')
Y = tf.placeholder(tf.float32, name='Y')


#初始化参数/权重
W = tf.Variable(tf.random_normal([1]), name='weight')
B = tf.Variable(tf.random_normal([1]), name='bias')
W_2 = tf.Variable(tf.random_normal([1]), name='weight_2')
W_3 = tf.Variable(tf.random_normal([1]), name='weight_3')

#计算预测结果
Y_pred = tf.add(tf.multiply(X, W), B)
Y_pred = tf.add(tf.multiply(tf.pow(X, 2), W_2), Y_pred)
Y_pred = tf.add(tf.multiply(tf.pow(X, 3), W_3), Y_pred)


#计算损失值
sample_num = xs.shape[0]
loss = tf.reduce_sum(tf.pow(Y_pred - Y, 2)) / sample_num


#初始化optimizer
learning_rate = 0.01
optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)


#指定迭代次数，并在session执行graph
n_sample = xs.shape[0]
init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    writer = tf.summary.FileWriter('./graphs/polynomial_reg', sess.graph)

    for i in range(600):
        total_loss = 0
        for x, y in zip(xs, ys):
            __, l = sess.run([optimizer, loss], feed_dict={X: x, Y: y})
            total_loss += l
        if i % 100 == 0:
            print('Epoch{0}:{1}'.format(i, total_loss/n_sample))

    writer.close()

    W, W_2, W_3, B = sess.run([W, W_2, W_3, B])

plt.scatter(xs, ys)
plt.plot(xs, xs**3*W_3 + xs**2*W_2 + xs*W + B, 'r')
plt.show()