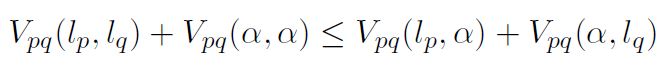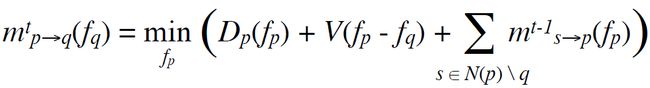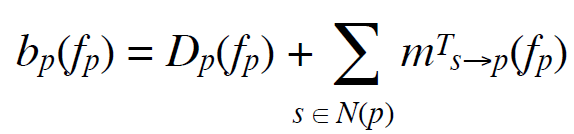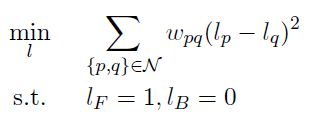图像处理中的全局优化技术(Global optimization techniques in image processing and computer vision) (一)

MulinB按：最近打算好好学习一下几种图像处理和计算机视觉中常用的 global optimization (或 energy minimization) 方法，这里总结一下学习心得。分为以下几篇：

1. Discrete Optimization: Graph Cuts and Belief Propagation (本篇)

2. Quadratic Optimization : Poisson Equation and Laplacian Matrix

3. Variational Methods for Optical Flow Estimation

4. TODO: Likelihood Maximization (e.g., Blind Deconvolution)

1. Discrete Optimization: Graph Cuts and Belief Propagation

很多图像处理和视觉的问题可以看成是pixel-labeling问题，用energy minimization framework可以formulate成以下能量方程：

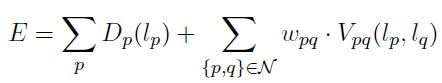
其中第一项叫data term (或叫unary term)，是将label l_p赋给像素p时的cost，第二项叫smoothness term (或叫pairwise term)，是每两个相邻pixel的labeling不同时产生的cost (w_pq是spatial varying weight，比如跟p和q的difference相关)。传统的smoothness term一般只考虑两两(pairwise)相邻的pixel，最近几年的CVPR和ICCV上开始出现很多higher-order MRF的研究，比如这位大牛的paper，这是题外话。这种energy minimization framework其实从概率的角度看，等价于求Markov Random Field (MRF) 的maximum a posteriori (MAP) 概率。求解这类energy minimization的方法，最流行的有两个，Graph Cuts和Belief Propagation。

1.1 Graph Cuts

刚开始学习Graph Cuts时，不知道到底这方法是从哪篇paper最早提出来的，因为在后来的paper里引用的参考文献一般指向好几个来源，这里先大致梳理一下参考文献。一般认为，将Graph Cuts引入图像处理领域的先驱paper是Greig等人1989年发表的[1]，不过貌似没有引起太大的注意。真正使Graph Cuts在图像领域风靡起来的是两个俄罗斯人(貌似是在Cornell做出的成果)，Yuri Boykov和Vladimir Kolmogorov，以及他们的导师Ramin Zabih。首先引起大家注意的是Boykov在ICCV 2001上的使用Graph Cuts解决Interactive Image Segmentation的paper[2]，以及这篇paper提到的一个max-flow算法[3] (该max-flow算法最早是发在2001年的一个CVPR Workshop上，后来扩展到TPAMI [3])。需要注意的是，这两篇paper里的Graph Cuts算法，只是针对只有两个label (待求变量是binary variable)的情况。而Boykov的2001 TPAMI paper[4]提出使用alpha expansion技术将多个label的问题转化成一系列的binary label问题去逼近，这使得Graph Cuts算法开始风靡起来。后来Kolmogorov的2004 TPAMI paper[5] 进一步讨论了什么样的能量方程可以被Graph Cuts优化，并给出了一个简单清晰的根据能量方程构造相应graph的算法，该算法基本成为被大家广泛使用的Graph Cuts算法。Boykov和Kolmogorov的代码可以从这里找到。

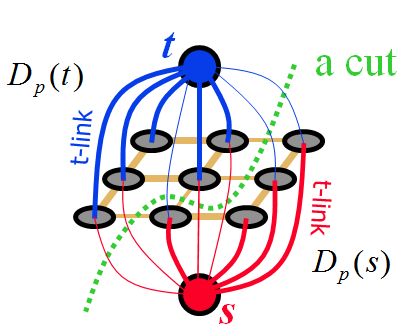
下面简单介绍一下Graph Cuts算法，先从binary label开始(见参考文献[2] [3])。顾名思义，Graph Cuts是将图像中的所有pixel以及两个label作为node，根据data cost和smoothness cost建立node之间的edge，这样构造一个(无向)graph，然后通过cut算法将整个graph切成两个分离的部分。如下图所示：

注意，图中的cut会切断它经过的所有edge(包括蓝色、红色、和土黄色的edge)。如果将两个label的node看成两个特殊的terminal，这样的一个cut会阻断所有s连往t的路径(edge)。在Boykov的ICCV 2001 paper [2]中，他证明了通过简单的方式构造这样的一个graph，如果能找到一个min-cut (即该cut经过的edge cost加起来在所有possible的cut中最小)，其实就是上面的能量方程的最小解 (见paper中的Theorem 1)。那么如何找到min-cut呢？

在图论里，有证明找到min-cut其实等价于找到max-flow，即从s流往t的最大流量。其实，min-cut等价于max-flow的intuition很简单，从一个terminal流往另一个terminal的最大流量，其瓶颈肯定是min-cut的位置。这里有个有意思的介绍，关于网络里s-t flow的计算。计算max-flow的经典算法主要有两种，一种是基于augmenting-path，一种是基于push-relabeling。在Boykov和Kolmogorov的TPAMI 2004 paper [3]里，介绍了一种基于augmenting-path，为了图像这种扁平graph量身定制的max-flow算法，通过实验证明了其效率，这里有他们的代码。

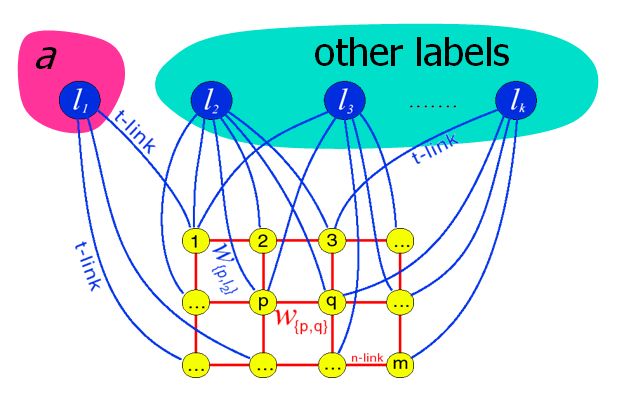
在解决multi-labeling问题时 (其实是更为普遍和常见的问题)，在能量方程满足某些特定的条件下(注意：该限定条件其实挺难满足，后面讨论！)，可以使用alpha expansion算法将其转化为一系列binary-labeling问题来逼近，参见Boykov TPAMI 2001 paper [4]。见下图：

这种alpha expansion思路很简单，当处理每一个label时(假设其为a)，将其他所有的label看成一个label package(假如称之为b)，这时问题就变成了binary-labeling。此时在进行cut时，如果一个原来是a的pixel被cut给b，将无法确定到底给该pixel具体哪一个label(由于b是个大杂烩)。所以在进行cut时，只允许原来是b的pixel被cut给a，也就是标记为a的pixel在expanding，这就是算法名字的来源。需要注意的是，为了使得这样的一次alpha expansion可以被max-flow算法计算出来，graph的构造比之前的binary-labeling要稍微复杂一些 (比如仅仅允许alpha expansion的话，有些跟b相连的edge weight要设成无穷大)。使用alpha expansion算法的步骤很简单，如下：

// alpha expansion algorithm pseudo-code
initialize labeling; 

while not converged
{
    for each label a in L
    {
        construct a graph;
        do max-flow cut;
        if energy is smaller than before, accept it; 
        else decline it; 
    }
}

值得注意的是，这种alpha expansion只是multi-labeling问题的近似求解，而之前的max-flow算法是binary-labeling问题的exact求解方法。而且，为了使得这种alpha expansion时的graph可以被构造出来，能量方程需要满足一定的限定条件，具体来说，是能量方程中的pairwise term函数V_pq需要满足某些限定条件。在Boykov TPAMI 2001 paper [4]中称之为V_pq必须是一个metric(类似于满足“距离”的定义，比如：可交换、满足三角不等式)。在Kolmogorov TPAMI 2004 paper [5] 中将其推广为V_pq必须是一个submodular函数(文中称之为regular，其实后来都称之为submodular)，即函数V_pq必须满足V(0,0) + V(1,1) <= V(0,1) + V(1,0)条件。该条件乍一看貌似很容易满足，特别是对于binary-labeling来说。然而，注意，在alpha expansion中，该条件变成了如下，

注意，其中l_p和l_q可能不一样。这样一来其实该条件没那么容易满足！比如常用的quadratic cost就不满足！常用的pairwise term的V_pq函数如下表所示 (Potts Model中delta函数是unit impulse函数)：

例如，quadratic cost时，l_p=3, l_q=10, a=5, 这时，上面条件里左侧第一项的值是49，第二项是0，不等式右侧第一项是4，第二项是25，显然不等式不成立！

另外需要一提的是，其实即使上述的条件不成立，仍然可以使用alpha expansion，使用的时候可以对一些不满足条件的项进行修改，这种技术在CVPR 05的一篇paper里提出[6]，叫做truncating，在这里的代码(文件energy.h，函数add_term2里)可以找到例子，代码非常简单：

//Truncating for non-submodualr term, code by Kolmogorov
//A, D, C, B分别是上述不等式的四项
if ( A+D > C+B) 
{
	Value delta = A+D-C-B;
        Value subtrA = delta/3;

        A = A-subtrA;
        C = C+subtrA;
        B = B+(delta-subtrA*2);
}

这种truncating之后的算法其实并不能保证最终结果是strong local minimum (注意，没有truncating的alpha expansion 只是能保证找到strong local minimum，不能保证是global mininum)，但是实际使用中效果不错。另外专门针对non-submodular进行优化的算法有QBPO，见Kolgoromov TPAMI 2007 paper [7]。

1.2 Belief Propagation

Belief Propagation是Graph Cuts的一个强劲对手，其渊源可以追溯到MIT在ICCV 2003上的paper [8]，比较这两种方法在stereo上的性能，结果貌似不分上下，Graph Cuts略胜一点点。后来大牛Richard Szeliski联合一堆MRF的experts搞了一个benchmark评测这些方法，见TPAMI 2008 paper[9]，和这个benchmark，上面有code可以下载，集成了很多算法，非常值得研究。结论是，Graph Cuts (alpha expansion)算法表现比较出色，另外Belief Propagation的一个改进算法叫Tree ReWeighted Message Passing (TRW-S)也表现出色，而Belief Propagation似乎表现不那么理想。不过其实其中除了Photomontage之外的其他比较中，基本都难分高下(在Photomontage中，alpha expansion完爆其他算法)。在实际使用中，至少在stereo的Middlebury benchmark上，Belief Propagation还是占了大多数席位。跟Graph Cuts相比，Belief Propagation至少有以下几个优点：

(1). 对能量方程不存在submodular限制;

(2). implement非常简单 (虽然理论比较难懂，但是算法implement非常之简单);

(3). 快速算法很快 (比如Hierarchical Belief Propagation，见Pedro Felzenszwalb的IJCV 2006 paper[10]，有代码在此).

下面简单介绍一下Belief Propagation算法，其背景知识可以参考Coursera上Daphne Koller的Probabilistic Graphical Model。Belief Propagation (BP)算法最早可以追溯到Pearl的书 [11]，该算法最初是设计在tree或者graph without cycles上通过message passing的方式计算MAP的(也就是上面提到的energy minimization)，在这种情况下，BP可以计算出exact的结果(其实等价于dynamic programming算法)。而在更为普遍的情况下，即graph中有cycle时，BP并不能保证可以converge，但是在很多情况下，可以converge到strong local minimum (有点类似alpha expansion)，见MIT大牛的TIT 2001 paper [12]。在这种情况下，BP一般被称为Loopy Belief Propagation，即graph中存在cycle使得message passing存在loop。另外，一般提到BP有两种，一种是max-product，一种是sum-product，前者是用来计算MAP的(max of probability product)，后者是用来计算marginal propability的，我们这里只讨论max-product (其实sum-product算法类似，只是计算message时稍有不同)。BP算法非常简单，流程如下：

//Belief Propagation Algorithm pseudo-code, suppose run T iterations
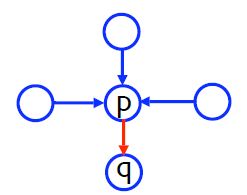
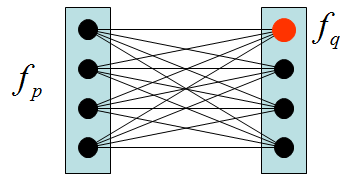
for (int t=0; t

最主要的步骤在于每次iteration中得message update。在计算某个pixel传递给另一个pixel的message时，要考虑上一个iteration中其他邻居pixel传给该pixel的message，如下图所示：

其中，蓝色箭头表示上一个iteration的message，红色箭头表示当前要计算的message。那么，message到底如何计算呢？假设label的candidate有L个(回忆一下，我们要解决的是pixel-labeling问题)，那么每条message包含有L个数值entry，表示的信息是“嘿，邻居，从我当前的状态看，你选择每个label的代价分别是...”。如果用f_q表示每个label，那么p传给q的message中的每个entry如下计算：

其中，t表示迭代数，f_p表示p的possible label(也有L个)，s是p的其余三个neighbors。非常简单，当要计算从p传给q的消息中关于f_q的entry时，考察每一个f_p，把data cost，smoothness cost (从f_p到f_q的cost), 其余neighbors传来的message统统加起来，在其中选择最小值即可(类似于dynamic programming算法)。图示如下：

可以看到，这个过程计算复杂度是O(L*L)。在Pedro Felzenszwalb的IJCV 2006 paper[10]里，针对一些常见的smoothness cost介绍了一些快速算法可以将复杂度减少到O(L)的计算复杂度，基本涵盖了上面表格里列出的cost类型。这样的message update经过T次迭代后，最后通过如下公式计算每个pixel的cost，

选择cost最小的label即为最终结果。

上面的message passing方式其实比较慢，一般需要很多次iteration才能使得message传递到全图。在Pedro Felzenszwalb的IJCV 2006 paper[10]里，提出使用multiscale/hierarchical的方式使得message更加快速的进行传递，这使得需要的iteration数量大大减小，使得BP的速度可以很快。

1.3 Other Related Techniques

Graph Cuts是从处理Interactive Image Segmentation (或叫Seeded Image Segmentation) 问题开始发家的 [2]，其他几种可以处理这种问题的方法有：Random Walker, Geodesic Shortest Path, Level Set Method等。这里简单介绍一下。

首先值得一提的是，SIGGRAPH 2004井喷了三篇基于Graph Cuts做interactive image editing的文章：GrabCut [13], Photomontage [14], Lazy Snapping [15]。其中以GrabCut影响力最大。GrabCut其实只是对Graph Cuts (Boykov ICCV 2001 [2]) 的一个扩展，使其变得更加robust。第一项扩展是将计算data cost从histogram扩展成用Gaussian Mixture Model，第二项扩展是将一次Graph Cuts计算扩展成迭代多次Graph Cuts。由于这样算法变得更加robust，其用户输入也可以变得较少，直接一个框就够了(当然使用fg/bg brush也可以，而且他们的system也可以用matting brush进行边界matting)，比如下图。

Random Walker图像分割(segmentation或matting)算法是另一种基于用户输入seeds (或者scribble) 的分割算法，见Leo Grady TPAMI 2006 paper[16]，注意，该算法在有些文献里叫做Random Walks图像分割算法，不过后来其作者倾向于叫其Random Walker算法，估计为了和随机游走算法(Random Walks)区分。其实该算法只是以Random Walks/Walker为出发点导出的，最终算法是一个quadratic optimization，有closed-form solution，可以通过求解一个线性方程组解决，所以算法可以很快(虽然数值求解大型线性方程组可能需要用到迭代算法，但是相当于其他迭代算法如Graph Cuts和Belief Propagation而言，求解线性方程组还是非常快的)。具体来讲，Random Walker的Motivation是：将图像看成是一个graph，给定用户输入的seeds，假设在每个pixel放置一个random walker，那么该random walker最先到达哪一个seed(概率上)，就将该pixel标记为那个seed的label。有相关理论证明(貌似一些关于potential theory或者circuit theory，whatever...)，求解这样的random walker模拟等价于求解Dirichlet problem，通过minimize相应的Dirichlet Integral，可以求得其解(即称为harmonic function)。而在graph上formulate该Dirichlet Integral，最后形式非常简单(Grady称之为combinatorial formulation，貌似其他的文献里有称之为discrete finite differential formulation)，这样，问题最终归结求解下面的非常简单的quadratic minimization问题：

其中，l是待求的labeling，l_F和l_B是用户标记的seeds处的label。其实该问题与后面我要谈的quadratic optimization里很多formulation很相似，尤其是Levin的Colorization和Closed-form Matting，这是后话。另外，该formulation还出现在diffusion map[17] 的问题中，这也是后话。Leo Grady后来还将Random Walker和Graph Cuts联系了起来 (ICCV 2007 paper[18])，其实从上面的formulation也可以大概看出来，上面的objective function只有smoothness term，而将其constraint移到objective function里就成为data term，跟Graph Cuts的唯一区别就是，Random Walker要解决的能量方程smoothness term是quadratic，而Graph Cuts可以用在不同的smoothness term的能量方程中(见上文的表格)。Random Walker有一个引人注意的特点，就是在weak boundary的表现非常出色(估计是因为其motivation跟potential有关系)，见下图例子。

从Random Walker的motivation可以想到，如果直接计算从每个pixel出发到seeds的最短路径(在路径上加入跟图像相关的weight时，这种路径为geodesic)，然后看pixel距离哪个seed近，就将pixel标记为那个seed的label。这就是基于Geodesic Distance的分割，见ICCV 2007 paper[19]。这种算法有个优点，就是所有pixel距离某一种seeds的geodesic distance可以非常快速的计算出来，用N表示pixel的个数，那么用Yatziv的Fast Marching[20] (在[19]中使用的算法，是Sethian的Fast Marching Method的快速实现)，或者更适用于并行计算的Parallel Marching [21] (在[22]中使用的算法，这里可以找到代码)，计算复杂度都可以达到O(N)。跟Random Walker相比，基于Geodesic Distance的方法速度更快，不过对seeds的位置依赖比较严重，而且在weak boundary表现也不会好，比如下面的例子。

提到Fast Marching Method，就不得不提另一个在图像领域影响很大的方法：Level Set Method。Level Set Method最早提出是为了解决boundary evolve的问题，比如用户在一个图像上画一个圈，然后这个圈根据图像内容进行演化，最终将一个物体圈出来，比如下图：

  

这种boundary evolve的问题最原始的方法是explicitly去跟踪boundary上的一些control points，而如果boudanry变化的过程中发生topological结构变化时(比如一个圈圈分裂成两个圈圈)，这种跟踪方式会很变得很难。Level Set Method就是为了解决这种难题。简单来讲，Level Set Method大概思路就是把原来二维的boundary evolve问题重新参数化为三维的surface evolve问题，新参数为笛卡尔坐标x-y以及时间t，这样新的问题成为一个在笛卡尔grid(即pixel grid)中的PDE，一般称为Hamilton-Jacob Equation，可以使用数值解法求出。其原理介绍可以参考Coursera上Guillermo Sapiro的Image and Video Processing，个人认为他讲的非常清晰易懂(可以直接看Section 6: Geometric PDEs)。

最后，再提一下Fast Marching Method。当上面的boundary evolve中曲线法向速度符号不变时(比如说boundary一直朝外扩张)，我们可以用更快速的方法来求解这个PDE：从boundary出发，在其所在的笛卡尔grid里计算并记录从boundary到每个pixel的距离(即到达时间)，如此得到一个类似于等高线图的map，而从这个map上，其实可以得到任意t时的boundary (取记录了某一个相同时间/距离的pixels)，如下图所示。这种map可以使用类似于Dijkstra最短路径算法的方法计算(一般称之为weve-front propagation方法)，或者用raster-scan的方法计算(更易于并行化)。Sethian的Fast Marching Method以及上文提到的Yatziv的快速实现[20]属于前者，而并行算法[21]属于后者。

1.4 Reference

[1]  D. Greig, B. Porteous, and A. Seheult, “Exact Maximum A Posteriori Estimation for Binary Images,” J. Royal Statistical Soc., 1989.

[2] Y. Boykov and M.-P. Jolly, “Interactive Graph Cuts for Optimal Boundary and Region Segmentation of Objects in N-D Images,” ICCV, 2001.

[3] Y. Boykov and V. Kolmogorov, “An Experimental Comparison of Min-Cut/Max-Flow Algorithms for Energy Minimization in Vision,” TPAMI, 2004.

[4] Y. Boykov, O. Veksler, and R. Zabih, “Fast Approximate Energy Minimization via Graph Cuts,” TPAMI, 2001.

[5] V. Kolmogorov and R. Zabih, “What Energy Functions can be Minimized via Graph Cuts,” TPAMI, 2004.

[6] C. Rother, S. Kumar, V. Kolmogorov, and A. Blake, “Digital Tapestry,” CVPR, 2005.

[7] V. Kolmogorov and C. Rother, “Minimizing Nonsubmodular Functions with Graph Cuts—A Review,” TPAMI, 2007.

[8] M. Tappen and W. Freeman, “Comparison of Graph Cuts with Belief Propagation for Stereo, Using Identical MRF Parameters,” ICCV, 2003.

[9] R. Szeliski, R. Zabih, D. Scharstein, O. Veksler, V. Kolmogorov, A. Agarwala, M. Tappen, and C. Rother. “A comparative study of energy minimization methods for markov random fields with smoothness-based priors.” TPAMI, 2008

[10] P. Felzenszwalb and D. Huttenlocher, “Efficient Belief Propagation for Early Vision,” IJCV, 2006.

[11] J. Pearl, Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann, 1988.

[12] Weiss, Y. and Freeman,W.T. 2001. “On the optimality of solutions of the max-product belief propagation algorithm in arbitrary graphs.” IEEE Transactions on Information Theory, 2001.

[13] C. Rother, V. Kolmogorov, and A. Blake, “‘GrabCut’—Interactive Foreground Extraction Using Iterated Graph Cuts,” SIGGRAPH, 2004.

[14] A. Agarwala,M. Dontcheva, M. Agrawala, S. Drucker, A. Colburn, B. Curless, D. Salesin, and M. Cohen, “Interactive Digital Photomontage,” SIGGRAPH, 2004.

[15] Y. Li, J. Sun, C.-K. Tang, and H.-Y. Shum, “Lazy snapping,” SIGGRAPH, 2004.

[16] L. Grady, “Random Walks for Image Segmentation,” TPAMI, 2006.

[17] R.R. Coifman, S. Lafon, A.B. Lee, M. Maggioni, B. Nadler, F. Warner, and S.W. Zucker, “Geometric Diffusions as a Tool for Harmonic Analysis and Structure Definition of Data: Diffusion Maps,” Proc. Nat’l Academy of Sciences USA, 2005.

[18] A.K. Sinop and L. Grady, “A Seeded Image Segmentation Framework Unifying Graph Cuts and Random Walker Which Yields a New Algorithm,” ICCV, 2007.

[19] X. Bai and G. Sapiro, “A Geodesic Framework for Fast Interactive Image and Video Segmentation and Matting,” ICCV, 2007.

[20] L. Yatziv, A. Bartesaghi, and G. Sapiro, “O(n) implementation of the fast marching algorithm,” Journal of Computational Physics, 2006.

[21] O. Weber, Y. Devir, A. Bronstein, M. Bronstein, and R. Kimmel,“Parallel algorithms for approximation of distance maps on parametric surfaces,” SIGGRAPH, 2008.

[22] A. Criminisi, T. Sharp, and C. Rother, “Geodesic Image and Video Editing,” TOG, 2010.