二叉树笔试题（一）

1、二叉树的前序遍历、中序遍历、后序遍历
思路：
在二叉树那篇文章里（ https://blog.csdn.net/Nan_Feng726/article/details/90904216 ） 已经介绍过，这里直接看代码：

private ArrayList<Integer> list;

    //1、前序
    private void preorder(TreeNode root) {
        if (root != null) {
            list.add(root.val);
            preorder(root.left);
            preorder(root.right);
        }
    }

    public List<Integer> preorderTraversal(TreeNode root) {
        list = new ArrayList<Integer>();
        preorder(root);
        return list;
    }

    //2、中序
    private void inorder(TreeNode root) {
        if (root != null) {
            inorder(root.left);
            list.add(root.val);
            inorder(root.right);
        }
    }

    public List<Integer> inorderTraversal(TreeNode root) {
        list = new ArrayList<Integer>();
        inorder(root);
        return list;
    }

    //3、后序
    private void postorder(TreeNode root) {
        if (root != null) {
            postorder(root.left);
            postorder(root.right);
            list.add(root.val);
        }
    }

    public List<Integer> postorderTraversal(TreeNode root) {
        list = new ArrayList<Integer>();
        postorder(root);
        return list;
    }

2、给定两个二叉树，编写一个函数来检验它们是否相同
思路：
判断两棵树是否相同，不仅需要判断根节点值是否相同，还需要递归判断根节点左右子树是否相同。考虑特殊情况，如果两棵子树都是空树，那么一定相同，如果其中一棵为空树，一棵不是空树，那么肯定不相同，看代码：

public boolean isSameTree(TreeNode p, TreeNode q) {
        if (p==null && q==null){
            return true;
        }
        if (p==null || q==null){
            return false;
        }
        return p.val == q.val
                && isSameTree(p.left,q.left)
                && isSameTree(p.right,q.right);
    }

3、如何判断两棵树互为镜像
思路：
两棵树是否互为镜像，除了判断根节点的值相同，还需要递归判断左子树等于右子树。如果两棵树都为空，那么它们互为镜像，如果只有其中一个为空，那么它们不是互为镜像，看代码：

public boolean isMirror(TreeNode p,TreeNode q){
        if (p==null && q==null){
            return true;
        }
        if (p==null || q==null){
            return false;
        }
        return p.val == q.val
                && isMirror(p.left,q.right)
                && isMirror(p.right,q.left);
    }

4、给定一个二叉树，检查它是否是镜像对称的（判断一棵树是否是对称二叉树）
思路：
判断一个二叉树是否镜像对称，可以转化为上题中判断根节点的左右子树是否镜像对称，左右子树如果镜像对称，说明该二叉树就是镜像对称的。需要注意的是，如果根节点为空，那么这棵二叉树也是对称二叉树。

public boolean isMirror(TreeNode p,TreeNode q){
        if (p==null && q==null){
            return true;
        }
        if (p==null || q==null){
            return false;
        }
        return p.val == q.val
                && isMirror(p.left,q.right)
                && isMirror(p.right,q.left);
    }
  
    public boolean isSymmetric(TreeNode root) {
        if(root==null){
            return true;
        }
        return isMirror(root.left,root.right);
    }

5、给定两个非空二叉树 s 和 t，检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。
示例：


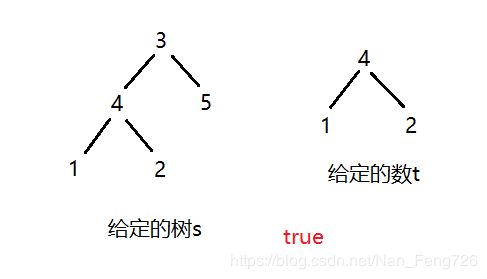
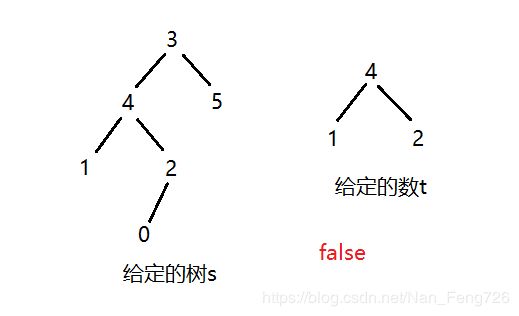
思路：
检查 t 是不是 s 的子树，首先判断 s 是不是一棵空树，如果 s 是空树，那么它没有任何子树。接着从根节点开始判断它们是不是同一棵树，如果是同一棵树，那么它就是自身的子树。如果不是同一棵树，就去它的左子树中查找有没有相同的树，没找到的话，再去右子树查找，都没找到说明 t 不是 s 的子树。
具体代码如下：

private boolean isSame(TreeNode p,TreeNode q){
        if (p==null && q==null){
            return true;
        }
        if (p==null || q==null){
            return false;
        }
        return p.val == q.val
                && isSame(p.left,q.left)
                && isSame(p.right,q.right);
    }
    private boolean find(TreeNode root,TreeNode t){
        if (root==null){
            return false;
        }
        if (isSame(root,t)){
            return true;
        }
        if (find(root.left,t)==true){
            return true;
        }
        return find(root.right,t);
    }
    public boolean isSubtree(TreeNode s, TreeNode t) {
        return find(s,t);
    }

6、求二叉树的最大深度
思路：
这道题在二叉树那篇文章里也介绍过，需要注意的就是最大深度是左右子树中高度较大的那个加一（加一是加上根节点所在层）。
直接看代码：

private static int height(Node root){
        //空树
        if (root==null){
            return 0;
        }else if (root.left==null && root.right==null){
            //一个节点，可选
            return 1;
        }else {
            //其它：max(left,right)+1
            int left = height(root.left);
            int right = height(root.right);
            return (left>right?left:right)+1;
        }
    }

7、给定一个二叉树，判断它是否是高度平衡的二叉树。
示例：

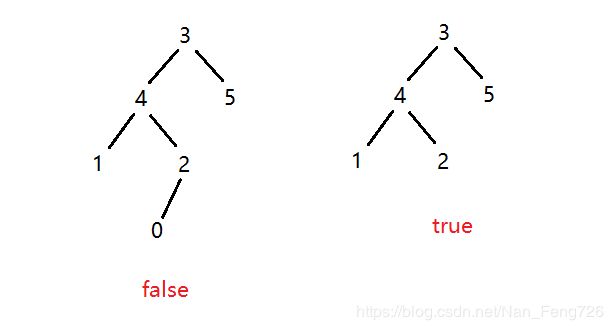
思路：
在说这道题之前，首先需要明确什么是平衡二叉树？

平衡二叉树：
平衡二叉搜索树又被称为AVL树（有别于AVL算法），且具有以下性质：
1）它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1
2）左右两个子树都是一棵平衡二叉树。
平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
最小二叉平衡树的节点总数的公式为： F(n)=F(n-1)+F(n-2)+1
（1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。）

根据平衡二叉树的特点，我们必须判断左右子树是否平衡，还需要判断左右子树的高度差是否小于等于1，代码比较容易理解，注意空树也是平衡二叉树：

public int height(TreeNode root){
        if (root==null){
            return 0;
        }
        return Math.max(height(root.left),height(root.right))+1;
    }
    public boolean isBalanced(TreeNode root) {
        if (root==null){
            return true;
        }
        if (isBalanced(root.left)==false){
            return false;
        }
        if (isBalanced(root.right)==false){
            return false;
        }
        int left = height(root.left);
        int right = height(root.right);
        int diff = left-right;
        if (diff<-1 || diff>1){
            return false;
        }
        return true;
    }