ACM--动态规划

动态规划dp算法

基本概念

动态规划算法通常用来求解具有最优性质的问题

• 将问题划分为几个子问题
• 将子问题进行求解,然后从若干个子问题的解里面得出原问题的解

例题分析

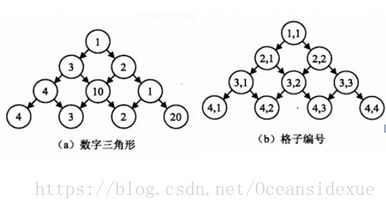
数字三角形

题目描述：
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。
对于每条路径，把路径上面的数加起来可以得到一个和，和最大的路径称为最佳路径。
你的任务就是求出最佳路径上的数字之和。
提示：可以将三角形存为二维数字，如右图所示那样哦
1.回溯法

#include 
#include 
#include 

using namespace std;

const int maxn = 105;
int d[maxn][maxn], a[maxn][maxn];
int T, n;

int dfs(int x, int y){
  // dfs(x, y) 返回从x,y 出发到末端点最大的值;
    if(x == n-1) return a[x][y];
    else {
        return a[x][y] + max(dfs(x+1,y), dfs(x+1, y+1));
    }

}

int main()
{
    scanf("%d", &T);
    while(T--){

        // 初始化;
        memset(d, 0, sizeof(d));
        // 输入数据
        scanf("%d", &n);
        for(int i = 0; i < n; ++i){
            for(int j = 0; j <= i; ++j)
                scanf("%d", &a[i][j]);
        }

        // 处理数据;
        int ans = dfs(0, 0);
        printf("%d", ans);
    }
}

2.动态规划算法
当前状态为(i,j)
定义d(i,j)为从(i,j)出发到底部的最大和

• 记忆法

int dfs1(int i,int j){
    memset(d, -1, sizeof(d));//将d里面的元素全部置为-1
    if(d[i][j]>=0)return d[i][j];
    else{
        return d[i][j]=a[i][j]+max(dfs1(i+1,j),dfs1(i+1,j+1));
    }
}

• 使用vis[i][j]数组

memset(vis, 0, sizeof(vis));
int dfs(int i,int j){
    if(vis[i][j])return d[i][j];
    else{
        vis[i][j]=1;
        d[i][j]=a[i][j]+max(d[i+1][j],d[i+1][j+1]);
} 

01背包问题

核心思想:
有两种情况:
第一种背包容量不够第i个物品不放入背包里面 则d[i][w]=d[i-1][w];
第二种 背包容量足够第i个物品放入背包里面则有两种取取得价值最大的一种选择

for(i=1;ifor(int j=1;jif(w[i]<=W){
                d[i][j]=max(d[i-1][j],d[i-1][W-w[i]]+v[i]);
                if(d[i][j]==d[i-1][W-w[i]]+v[i])x[i]=1;
                else x[i]=0;
            }
            else d[i][j]=d[i-1][j];
        }
    }

最长公共子序列

A subsequence of a given sequence is the given sequence with some elements (possible none) left out. Given a sequence X = < x1, x2, …, xm > another sequence Z = < z1, z2, …, zk > is a subsequence of X if there exists a strictly increasing sequence < i1, i2, …, ik > of indices of X such that for all j = 1,2,…,k, x ij = zj. For example, Z = < a, b, f, c > is a subsequence of X = < a, b, c, f, b, c > with index sequence < 1, 2, 4, 6 >. Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y

Input
The program input is from the std input. Each data set in the input contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct.

Output
For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
Sample Input

abcfbc         abfcab
programming    contest 
abcd           mnp

Sample Output

4
2
0

#include 
#include 
#include 
#define Max( a, b ) (a) > (b) ? (a) : (b)
using namespace std;

char s1[1005], s2[1005];

int dp[1005][1005];

int main()
{
    int len1, len2;
    while( scanf( "%s %s", s1, s2 ) != EOF )
    {
        memset( dp, 0, sizeof(dp) );
        len1 = strlen( s1 ), len2 = strlen( s2 );
        for( int i = 1; i <= len1; ++i )
        {
            for( int j = 1; j <= len2; ++j )
            {
                if( s1[i-1] == s2[j-1] )
                {
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                else
                {
                    dp[i][j] = Max ( dp[i-1][j], dp[i][j-1] );
                }
            }
        }
        printf( "%d\n", dp[len1][len2] );
    }
    return 0;
}