Udacity cs344Unit 3-Introduction to Parallel Programming笔记(超详细,CUDA,并行,GPU)
1.课程目标
如何分析GPU算法的速度和效率(speed and efficiency)
三个新的基本算法:归约,扫描和直方图(reduce,scan and histogram)
2.
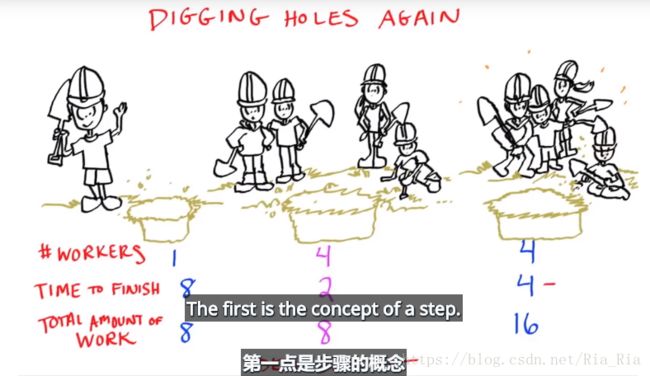
3.再看之前讲的例子
考虑两件事
介绍几个概念
a.步骤(step):指的是 单人!完成某特定计算(比如挖洞)所需时间
b.工作总量(total amount of work):所有参与员工完成计算量的总值
也就是,人数 * 步数 = 工作总量
4.谈论算法时,将讨论两个成本
a.step complexity(步骤复杂度):一共分成几个步骤得到了最终结果,那个步骤数量
b.work complexity(工作复杂度):一共进行了多少次计算?
我们会用step complexity 或者work complexity来衡量一个算法,而这两个指标通常与input的大小是有关联的
5.
从数学定义开始
有两个输入(一个数组和一个运算符)运算符要具有两个性质:二元性和可结合性
6.
先看串行的归约(每一个操作都依赖前一个操作)
操作次数为4次,共计4 steps
这意味着工作复杂度(与节点数目一致)和步骤复杂度(操作总次数)都是和input成正比的
7.并行归约(就是想办法给他凑成可以一同运算的,互相不依赖的——改变运算次序)结合性保证了次序改变,结果不受影响
如果只有p个处理器,需要多少步,才能处理n个输入
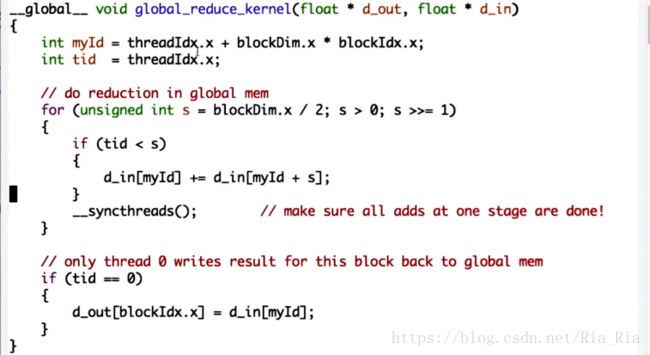
8.试着编写一下这个代码
9.
举一个现实中用到scan的例子:收支平衡(计算余额)
你输入一个,我得一个结果
9.数学描述
介绍一个概念:某个运算符的标识元素(identify element):比如“+”的identify element 是0
10.串行的for循环,n是几就进行了多少次操作,就是多少个步骤,并行怎么计算?
a.我们怎么计算扫描和并行(的步骤和操作次数)
b.我们怎么能尽量降低工作和步骤复杂度?
在这两个小问题之前
先来看一个大问题:
在并行有这么多种操作的前提下,我们为啥偏偏先关注扫描的并行化?
当每次只能进行一次计算的时候,是没办法并行的(都要依赖前面一次的结果)
但是像这类的计算,通常可以转化成扫描的形式
当可以用扫描的方式来刻画计算的时候,就有用啦!
因为:我们可以使扫描并行化!并且在GPU上飞快运行!
我们要做的是:找到能转化成scan的运算模型!把问题从不适合GPU的转化成适合GPU的
11.当找到模型后,怎么实现扫描呢?
有两种方法
a.不包含扫描(exclusive scan):计算结果中不包含当前元素
b.包含扫描(include scan)
把包含扫描转化成不包含
12.测验:scan的复杂度
步骤复杂度:就看最复杂的那个需要多少步骤就行了
工作复杂度:每一次运算都加起来的总和【0+1+2+...+(n-1)】
由于工作复杂度太高,所以聪明的人们又想出了两种算法!
12.Hill + Steele VS Blelloch
a.
先看步骤复杂度,是logn(一般采用了分治思想的,复杂度都会是logn,因为砍掉了一些数据没有切实的计算,而这里的底数也不必在意,就像是若复杂度为n的平方,也不必在意前面的系数一样)
工作复杂度:是这个矩形的面积,用长n乘上宽logn
b. 三角矩形法(想着传手画图)【这个很像郭老师讲的归约和回溯啊,第一阶段进行归约,得出最后想要的结果,第二阶段再去找凑成这个结果的路径是什么】
测试 max操作
看复杂度
工作量是不是也是2倍的?比logn要小嘛?
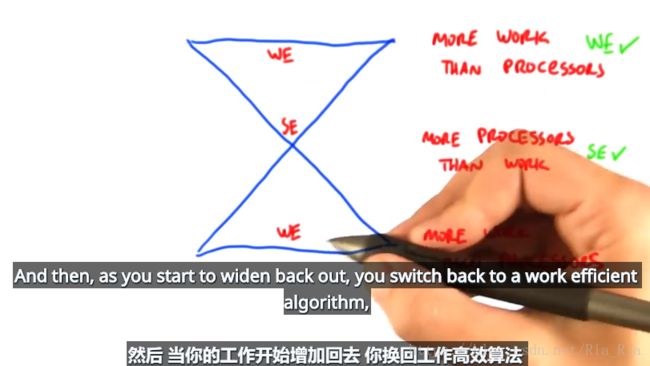
13.给你一点直觉,在两个算法分别在工作复杂度和步骤复杂度上各占优势时候,要怎么选择
a.工作多于处理器:可以牺牲步骤,换取工作量
b.处理器多于工作:愿意牺牲工作量来换取更少的步骤(选择步骤复杂度低的)
在并行算法里有很多的沙漏模型(比如刚刚的三角矩形算法就是这样):那么我们可以在不同的阶段采用不同的算法,来保证总体运行通常,效率最高
14.直方图
(就是统计介于某个段值内的实体个数)
如果我知道我的身高,想知道比我矮的有多少个,就用exclusive scan
15.实现过程
16.代码实现
在线性程序中
看并行的为啥会出错:有两个线程同时运行的风险
所以暴力简单法不可行
17.看仨有效的法子
a.改成原子操作就可以啦
这种方法在bin(也就是各个段盛放的容器)个数很大是时候,会很好用。因为原子操作会限制并行度的大小
推出b
b.分本地内存,再归约
不需要原子操作
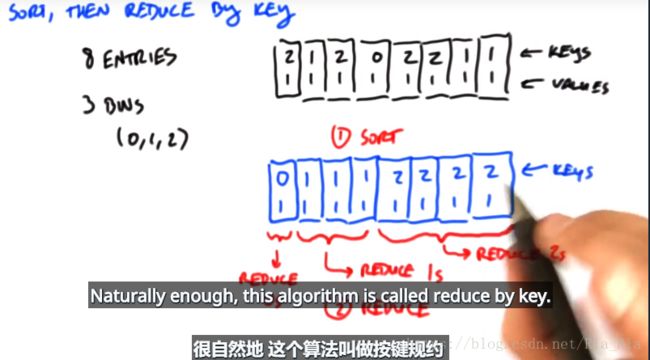
c.先排序再归约
18最终思想:由于这三种方法(没有最好,各有利弊),所以把这三个方法分别用于不同的阶段就好啦
a.大多数线程试图访问bin存储器时候,原子操作不适用,因为会有大量线程处于等待之中(bin是直方图下面的段数)
所以就先分block,因为在共享内存里是不需要进行原子操作的,只有当最后合并时候,才需要进行原子操作
19.