数据结构与算法(2)
栈的顺序存储结构
栈的定义
栈是限定仅在表尾进行插入和删除操作的线性表
我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom)
不含任何数据元素的栈称为空栈
栈又称为后进先出的线性表,简称LIFO结构
定义中说的是在线性表的表尾进行插入和删除操作,这里表尾是指栈顶,而不是栈底
栈的插入操作,也叫做进栈,也称压栈,入栈
栈的删除操作,也叫做出栈,也称弹栈
栈接口Stack的定义
package com.study.zhan;
/**
* Stack是栈的接口
* */
public interface Stack {
/**
* 获取栈中元素的个数
* @return 栈中的元素个数
* */
public int getSize();
/**
* 判断当前栈是否为空
* @return 是否为空值
* */
public boolean isEmpty();
/**
* 进栈一个元素e
* @param e即将进栈的元素
* */
public void push(E e);
/**删除最后一个元素
*
* */
public E pop();
/**
* 获取最后一个元素
* */
public E peek();
/**
* 清空栈
* */
public void clear();
}
栈的顺序存储结构ArrayStack的定义
ArrayStack完全可以把ArrayList一个工具,这两者是聚合关系
package com.study.zhan;
import com.study.shuzu.ArrayList;
public class ArrayStack implements Stack {
/**
* 栈的实现完全可以借助于ArrayList
* */
private ArrayList list;
/**
* 创建一个默认大小的栈(顺序表)
* */
public ArrayStack() {
list = new ArrayList();
}
/**
* 创建一个容量为指定capacity大小的栈(顺序表s)
* */
public ArrayStack(int capacity) {
list = new ArrayList(capacity);
}
/**
* 获取有效元素的个数
* */
@Override
public int getSize() {
return list.getSize();
}
/**
* 判断是否为空栈
* */
@Override
public boolean isEmpty() {
return list.isEmpty();
}
/**
* 给栈里添加数据元素
* */
@Override
public void push(E e) {
list.addLast(e);
}
/**
* 删除栈顶元素
* */
@Override
public E pop() {
return list.removeLast();
}
/**
* 获取栈顶数据元素
* */
@Override
public E peek() {
return list.getLast();
}
/**
* 删除栈里面的所有数据元素,变为空栈
* */
@Override
public void clear() {
list.clear();
}
/**
* 判断两个栈是否相等
* */
@Override
public boolean equals(Object obj) {
if(obj == null) {
return false;
}
if(obj == this) {
return true;
}
if(obj instanceof ArrayStack) {
ArrayStack stack = (ArrayStack) obj;
return list.equals(stack.list);
}
return false;
}
/**
* 重写toString方法,用来显示数据元素栈
* */
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("ArrayStack: size="+ getSize() +",capacity="+ list.getCapacity() +"\n");
if(isEmpty()) {
sb.append("[]");
} else {
sb.append('[');
for(int i = 0; i < getSize();i++) {
sb.append(list.get(i));
if(i == getSize()-1) {
sb.append(']');
} else {
sb.append(',');
}
}
}
return sb.toString();
}
}
栈的测试类
package com.study.zhan;
import java.util.Arrays;
public class TestStack {
public static void main(String[] args) {
ArrayStack stack = new ArrayStack();
System.out.println(stack);
for(int i = 1;i < 7;i++) {
stack.push(i);
// System.out.println(stack.isEmpty());
}
System.out.println(stack.getSize());
System.out.println(stack);
ArrayStack stack2 = new ArrayStack(20);
stack2.push(1);
stack2.push(2);
stack2.push(3);
stack2.push(4);
stack2.push(5);
stack2.push(6);
System.out.println(stack2);
System.out.println(stack2.peek());
stack2.pop();
System.out.println(stack2);
System.out.println(stack.equals(stack2));
}
}
双端栈的顺序存储结构
双端栈的定义
是指将一个线性表的两端当做栈底分别进行入栈和出栈操作

双端栈的顺序存储结构ArrayStackDoubleEnd的定义
package com.study.zhan;
import com.study.shuzu.ArrayList;
public class ArrayStackDoubleEnd implements Stack {
enum Direction{
LEFT,RIGHT;
}
private E[] data;
private int leftTop; //左端栈的栈顶开始在-1
private int rightTop; //右端栈的栈顶开始在data.length
private static int DEFAULT_SIZE = 10;
public ArrayStackDoubleEnd() {
this(DEFAULT_SIZE);
}
public ArrayStackDoubleEnd(int capacity) {
data = (E[]) new Object[capacity];
leftTop = -1;
rightTop = data.length;
}
/**
* 判断双端栈是否满
* */
private boolean isFull() {
return leftTop+1 == rightTop;
}
/**
* 先指定的端口进栈元素
* */
public void push(Direction dir,E e) {
if(isFull()) {
//扩容
resize(data.length * 2);
}
if(dir == Direction.LEFT) {
data[++leftTop] = e;
} else {
data[--rightTop] = e;
}
}
//双指针解题思想
private void resize(int newLen) {
E[] newData = (E[]) new Object[newLen];
for(int i =0;i <= leftTop;i++) {
newData[i] = data[i];
}
int index = data.length - 1;
int i;
for(i = newData.length - 1;i >= newData.length - data.length + rightTop;i--) {
newData[i] = data[index--];
}
rightTop = i + 1;
data = newData;
}
/**
* 从指定的端口出栈元素
* */
public E pop(Direction dir) {
if(dir == Direction.LEFT) {
if(leftTop == -1) {
throw new IllegalArgumentException("左端栈为空");
}
E e = data[leftTop--];
if(getSize() <= data.length / 4 && data.length > DEFAULT_SIZE) {
resize(data.length / 2);
}
return e;
} else {
if(rightTop == data.length) {
throw new IllegalArgumentException("右端栈为空");
}
E e = data[rightTop++];
if(getSize() <= data.length / 4 && data.length > DEFAULT_SIZE) {
resize(data.length / 2);
}
return e;
}
}
/**
* 从指定的端口获取栈顶元素
* */
public E peek(Direction dir) {
if(dir == Direction.LEFT) {
if(leftTop == -1) {
throw new IllegalArgumentException("左端栈为空");
}
return data[leftTop];
} else {
if(rightTop == data.length) {
throw new IllegalArgumentException("右端栈为空");
}
return data[rightTop];
}
}
/**
* 获取指定端口栈的元素个数
* */
public int getSize(Direction dir) {
if(dir == Direction.LEFT) {
return leftTop + 1;
} else {
return data.length - rightTop;
}
}
/**
* 判断指定端口的栈是否为空
* */
public boolean isEmpty(Direction dir) {
if(dir == Direction.LEFT) {
return leftTop == -1;
} else {
return rightTop == data.length;
}
}
/**
* 清空指定端口的栈
* */
public void clear(Direction dir) {
if(dir == Direction.LEFT) {
leftTop = -1;
} else {
rightTop = data.length;
}
}
/**
* 获取 左端栈和右端栈元素的总和
* */
@Override
public int getSize() {
return getSize(Direction.LEFT)+getSize(Direction.RIGHT);
}
/**
* 判断左端栈和右端栈是否全为空
* */
@Override
public boolean isEmpty() {
return isEmpty(Direction.LEFT)&&isEmpty(Direction.RIGHT);
}
/**
* 如果说那端少就进入那端
* */
@Override
public void push(E e) {
if(isFull()) {
resize(data.length * 2);
}
if(getSize(Direction.LEFT) <= getSize(Direction.RIGHT)) {
push(Direction.LEFT,e);
} else {
push(Direction.RIGHT,e);
}
}
/**
* 如果那端多就弹那端,一样多默认弹左边
* */
@Override
public E pop() {
if(isEmpty()) {
throw new IllegalArgumentException("两端栈为空");
}
if(getSize(Direction.LEFT) > getSize(Direction.RIGHT)) {
return pop(Direction.LEFT);
} else {
return pop(Direction.RIGHT);
}
}
/**
* 那端多获取那端,一样多默认左
*/
@Override
public E peek() {
if(isEmpty()) {
throw new IllegalArgumentException("双端栈为空");
}
if(getSize(Direction.LEFT) > getSize(Direction.RIGHT)) {
return peek(Direction.LEFT);
} else {
return peek(Direction.RIGHT);
}
}
/**
* 左右两端都清空
* */
@Override
public void clear() {
clear(Direction.LEFT);
clear(Direction.RIGHT);
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("ArrayStackDoubleEnd: size="+ getSize() +",capacity="+ data.length +"\n");
if(isEmpty()) {
sb.append("[]");
} else {
sb.append('[');
int count = 0;
for(int i = 0;i <= leftTop;i++) {
sb.append(data[i]);
count++;
if(count == getSize()) {
sb.append(']');
} else {
sb.append(',');
}
}
for(int i = rightTop;i < data.length;i++) {
sb.append(data[i]);
count++;
if(count == getSize()) {
sb.append(']');
} else {
sb.append(',');
}
}
}
return sb.toString();
}
/**
* 定义一个新的双端栈与前一个进行比较,看是否相等,比较的两双端栈的内容
* */
@Override
public boolean equals(Object obj) {
if(obj == null) {
return false;
}
if(obj == this) {
return true;
}
if(obj instanceof ArrayStackDoubleEnd) {
ArrayStackDoubleEnd stack = (ArrayStackDoubleEnd) obj;
if(getSize() == stack.getSize()) {
ArrayList list1 = new ArrayList(getSize());
ArrayList list2 = new ArrayList(getSize());
//拼接当前栈的左部分元素
for(int i = 0;i <= leftTop;i++) {
list1.addLast(data[i]);
}
//拼接当前栈的右部分元素
for(int i = rightTop;i < data.length;i++) {
list1.addLast(data[i]);
}
//拼接传入栈的左部分元素
for(int i = 0;i <= stack.leftTop;i++) {
list2.addLast(stack.data[i]);
}
//拼接传入栈的右部分元素
for(int i = stack.rightTop;i < stack.data.length;i++) {
list2.addLast(stack.data[i]);
}
return list1.equals(list2);
}
}
return false;
}
}
双端栈的顺序存储结构—入栈操作
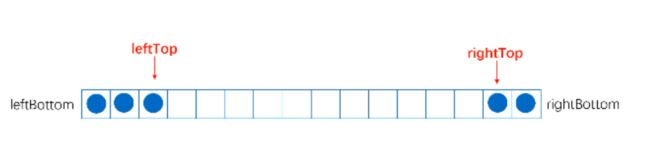
数据元素分别一左一右进入栈,这里存在两个栈顶一个左栈顶一个右栈顶,同时也有两个栈底,一个左栈底一个右栈底
双端栈的顺序存储结构—出栈操作
同样也是那边栈的元素较少,这边栈内元素就不出
双端栈的测试类
package com.study.zhan;
import com.study.zhan.ArrayStackDoubleEnd.Direction;
public class TestStackDoubleEnd {
public static void main(String[] args) {
ArrayStackDoubleEnd stack = new ArrayStackDoubleEnd();
for(int i = 1;i <= 5;i++) {
stack.push(Direction.LEFT, i);
}
System.out.println(stack);
for(int i = 6;i <= 10;i++) {
stack.push(Direction.RIGHT, i);
}
System.out.println(stack);
for(int i = 11; i <= 15;i++) {
stack.push(i);
}
System.out.println(stack);
for(int i = 1;i <= 10;i++) {
stack.pop();
}
System.out.println(stack);
ArrayStackDoubleEnd stack1 = new ArrayStackDoubleEnd();
stack1.push(Direction.LEFT, 1);
stack1.push(Direction.LEFT, 2);
stack1.push(Direction.LEFT, 3);
stack1.push(Direction.RIGHT, 6);
stack1.push(Direction.RIGHT, 7);
System.out.println(stack.equals(stack1));
System.out.println(stack1.peek());
}
}
队列的顺序存储结构
队列的定义
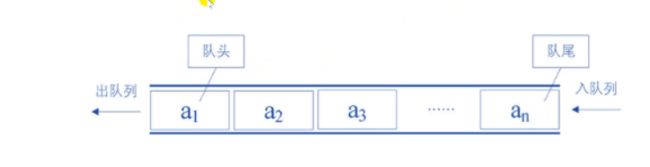
队列是指只允许在一端进行插入操作,而另一端负责进行删除操作的线性表
队列是一种先进先出的线性表,简称FIFO
允许插入的一端称为队尾,允许删除的一端称为对头
队列接口Queue的定义
package com.study.duilie;
public interface Queue {
public int getSize();
public boolean isEmpty();
public void clear();
/**
* 入队一个新元素
* */
public void enqueue(E e);
/**
* 出队一个元素
* */
public E dequeue();
/**
* 获取队首元素(不删除)
* */
public E getFront();
/**
* 获取队尾元素(不删除)
* */
public E getRear();
}
队列的顺序存储结构ArrayQueue的定义
package com.study.duilie;
import com.study.shuzu.ArrayList;
public class ArrayQueue implements Queue{
private ArrayList list;
public ArrayQueue() {
list = new ArrayList();
}
public ArrayQueue(int capacity) {
list = new ArrayList(capacity);
}
@Override
public int getSize() {
return list.getSize();
}
@Override
public boolean isEmpty() {
return list.isEmpty();
}
@Override
public void clear() {
list.clear();
}
@Override
public void enqueue(E e) {
list.addLast(e);
}
@Override
public E dequeue() {
return list.removeFirst();
}
@Override
public E getFront() {
return list.getFirst();
}
@Override
public E getRear() {
return list.getLast();
}
}
队列的顺序存储结构—入队操作O(1)
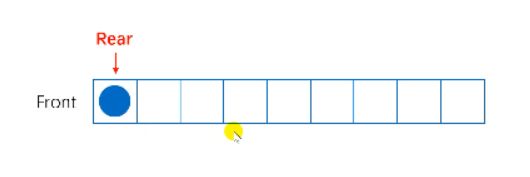
入队就相当于是给ArrayList.addLast
队列的顺序存储结构—出队操作O(n)

出队就相当于ArrayList.removeFirist
循环队列的顺序存储结构
队列顺序存储结构的弊端
队列的顺序存储结构本身是由ArrayList实现的
在数据元素入队的时候,相当于在Array List表尾添加元素
在数据元素出队的时候,相当于在ArrayList表头删除元素
很明显,入队的时间复杂度O(1),出队的时间复杂度O(n)
线性表增删数据元素时间复杂度都是O(n),但是这个是按平均算的
队列的出队时间复杂度O(n),可不是按平均算的,因为每次出队都是O(n)
优化第一步
队头指针和队尾指针随着元素的变化而移动,这样入队和出队操作都将是O(1)
优化第二步
当队尾或队头指针达到尾部时,如果需要后移重新指向表头
注意:队列满的条件为:(Rear + 1) % n == Front
队列空的条件为:Rear == Front
优化第三步
将一个空间预留出来不存任何元素,尾指针始终指向这个null空间
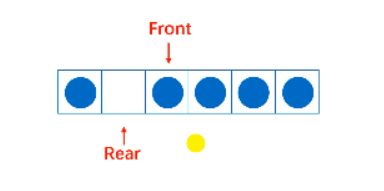
循环队列的定义
创建ArrayQueueLoop该类还是需要继承Queue接口
package com.study.duilie;
public class ArrayQueueLoop implements Queue {
private E[] data;
private int front;
private int rear;
private int size;
private static int DEFAULT_SIZE = 10;
/**创建一个默认长度为10的数组*/
public ArrayQueueLoop() {
this(DEFAULT_SIZE);
}
/**指定一个长度的数组*/
public ArrayQueueLoop(int capacity) {
data = (E[]) new Object[capacity + 1];
front = 0;
rear = 0;
size = 0;
}
/**直接访问数据元素个数*/
@Override
public int getSize() {
return size;
}
/**判断队列是否为空*/
@Override
public boolean isEmpty() {
return front == rear && size == 0;
}
/**清空队列*/
@Override
public void clear() {
size = 0;
front = 0;
rear = 0;
//与其缩容清空不如重新创建数组
}
@Override
public void enqueue(E e) {
if((rear + 1) % data.length == front) {
resize(data.length * 2 - 1);
}
data[rear] = e;
rear = (rear + 1) % data.length;
size++;
}
private void resize(int newLen) {
E[] newData = (E[]) new Object[newLen];
int index = 0; //新数组的角标
for(int i = front;i != rear ;i = (i + 1) % data.length) {
newData[index++] = data[i];
}
front = 0;
rear = index;
data = newData;
}
@Override
public E dequeue() {
if(isEmpty()) {
throw new IllegalArgumentException("队列为空");
}
E e = data[front];
front = (front + 1) % data.length;
size--;
if(size <= data.length / 4 && data.length > DEFAULT_SIZE) {
resize(data.length / 2 + 1);
}
return e;
}
/**获取队头元素*/
@Override
public E getFront() {
return data[front];
}
/**获取队尾元素*/
@Override
public E getRear() {
return data[(data.length + rear - 1) % data.length];
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("ArrayQueueLoop: size=" + getSize() +",capacity=" + (data.length - 1) +"\n");
if(isEmpty()) {
sb.append("[]");
} else {
sb.append('[');
for(int i = front; i != rear;i = (i+1) % data.length) {
sb.append(data[i]);
if((i+1) % data.length == rear) {
sb.append(']');
} else {
sb.append(',');
}
}
}
return super.toString();
}
}
循环队列测试类
package com.study.duilie;
public class TestArrayQueueLoop {
public static void main(String[] args) {
ArrayQueueLoop queue = new ArrayQueueLoop();
for (int i = 1; i <= 15; i++) {
queue.enqueue(i);
}
System.out.println(queue);
for (int i = 1; i <= 10; i++) {
queue.dequeue();
}
System.out.println(queue);
System.out.println(queue.getSize());
System.out.println(queue.getFront());
System.out.println(queue.getRear());
}
}