数据结构与算法专题之线性表——链表(二)双向链表
本文是线性表之链表第二弹——双向链表。在学习本章节之前,应该首先学习并掌握链表的概念及单链表的原理和实现,还未学习的小伙伴请移步上一篇文章,传送门:
数据结构与算法专题之线性表——链表(一)单链表
能看到这里,我就默认你学会了单链表并且理解了链表的基本概念,下面我们开始双向链表的学习。
双向链表的概念及结构
基本概念
双向链表,顾名思义,就是拥有前后两个方向的链表。由前面的单链表学习可知,单链表只有一个指向后置元素的指针域,也就决定了单链表只可以从前向后遍历反之则不行。所以看到这里大家可能已经想到了,双向链表与单链表结构的基本区别就是多了一个指向前置结点的指针域,没错就是这样。
双向链表有着更为灵活的访问方式,我们C++ STL内置的list实际上就是一个双向链表。
结点结构
参照单链表,我们可以把双向链表的结点结构定义如下图:
可见,双向链表需定义两个指针域,分别指向前置结点和后置结点,代码如下:
template
struct DNode
{
T data;
DNode *next, *previous;
}; 类结构
与单链表类似,双向链表包含如下几个基本操作:
(1) 尾部插入:push_back
(2) 头部插入:push_front
(3) 任意位置插入:insert
(4) 删除index位置元素: del
(5) 获取任意位置元素:get(这里我们依然是获取元素指针)
(6) 获取指定元素第一次出现的位置:find
类的结构代码如下:
template
class DList
{
private:
DNode *head, *tail;
int cnt;
public:
DList()
{
head = new DNode;
tail = head;
head->next = NULL;
head->previous = NULL;
cnt = 0;
}
void push_back(T elem); // 尾部插入
void push_front(T elem); // 头部插入
void insert(T elem, int index); // 向index位置插入
void del(int index); // 删除index位置的元素
DNode* get(int index); // 获取index位置的元素指针
DNode* find(T elem); // 获取elem第一次出现的位置的元素指针
int size(); // 获取链表的大小
void each(char split, int method); // 遍历输出链表,以split参数为间隔,method为0正向,为1反向,默认0
}; 下面我们根据上述定义来依次讲解各操作,如果你需要其他的一些操作,可以在学习了本章以后自己动手编码实现~
双向链表的实现
1. 尾部插入(push_back)
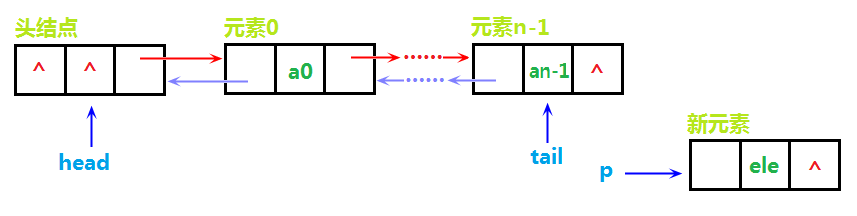
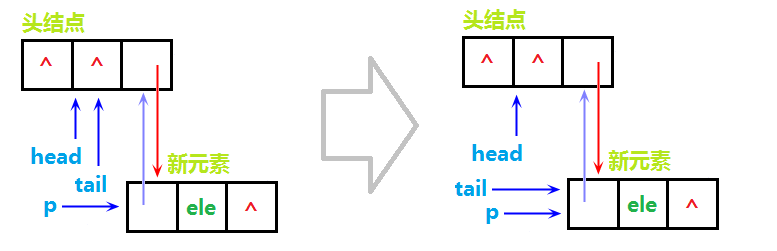
与单链表类似,需要先实例化一个结点p,并为结点next指针域赋NULL,如下图:
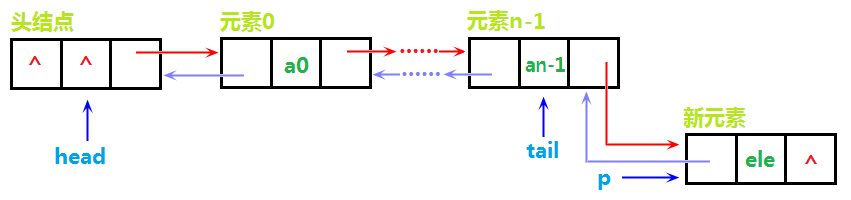
然后将tail的next域指向p,p的previous指向tail,使得它俩相互链接,如图:
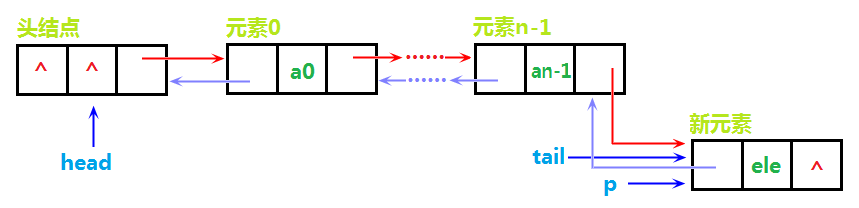
最后,将tail指针指向p即可,如图:
至此,完成了双链表尾部插入操作,很简单吧?代码如下:
template
void DList::push_back(T elem) // 尾部插入
{
DNode *p = new DNode;
p->data = elem;
p->next = NULL;
p->previous = tail;
tail->next = p;
tail = p;
cnt++;
} 2. 头部插入(push_front)
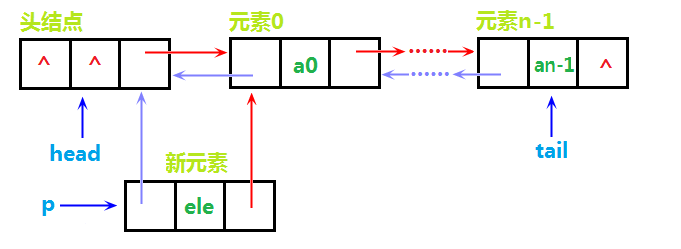
头部插入,与单链表也是类似的,同样第一步需要实例化一个结点p并赋值,这里不画图了,第二步开始,由于是头部插入,所以元素应该插在头结点和首元素结点之间,我们应该先让p结点的next域指向首元素结点,previous域指向头结点,把结点的两个指针域想象成“双手”,也就是让p的“双手”“牵住”前后两个结点。但注意红色标记的文字部分,如果链表是空的,则不存在元素0,也就是说p的next域应赋值空,但是这里我们无需特别判断,只需执行p->next=head->next,因为如果链表是空的话 ,head->next恰好是NULL,如图所示:
然后,只要p的“双手”牵住了头结点和元素0结点,我们就不怕他们“跑掉”了,然后我们再让头结点的next域指向p,元素0结点的previous域指向p,这里需要注意的是,如果插入前链表为空,则不存在元素0,也就不存在红色标记文字的那一步,但是,记得移动尾指针!看图!
特殊情况!与单链表一样,插入前无元素的,需要在插入后移动尾指针!看图:
好了,头部插入完成,上代码:
template
void DList::push_front(T elem) // 头部插入
{
DNode *p = new DNode;
p->data = elem;
p->next = head->next; // 右手牵着head的next
p->previous = head; // 左手牵着head
if(head->next != NULL) // head后有结点
{
head->next->previous = p; // head后置结点的前置结点改为p
}
head->next = p;
if(cnt == 0) // 无元素,移动尾指针
{
tail = p;
}
cnt++;
} 3. 任意位置插入(insert)
向任意位置插入,同样找出两种特殊情况,假设链表长度为n,即在0位置插入和在n位置插入为特殊情况,0插入相当于push_front,n插入相当于push_back(关于为啥是n而不是n-1,在前面单链表的insert那里已经介绍过了,自己移步去看~),其他属通常情况。
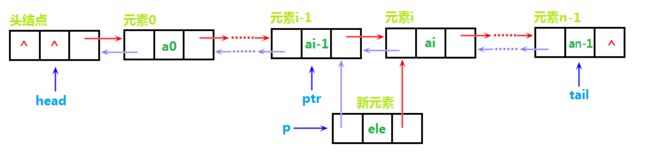
假设链表含有n个元素,要在位置i插入元素(i != 0 && i != n),如图所示:
插入方式与头部插入差不多,而且这是双向链表,元素指针的不仅可以向后移动,还可以向前移动,灵活的很~所以在位置i插入,实际上就是插在元素i-1和元素i之间,同样,先搞一个ptr指针初始化为head,向后移动i次即指向i-1元素,图不画了与单链表那个差不多,然后将新元素p分别与i-1和i“牵手”,如图:
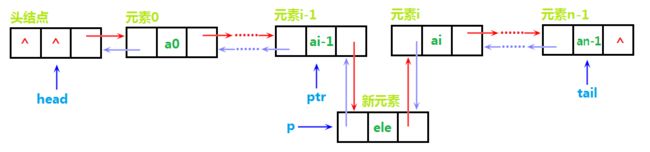
然后,p都主动牵手了,i和i-1你们俩干啥呢?所以他们俩的手就要分开,去牵p的手咯,看图:
好啦,牵手成功,皆大欢喜了,上代码:
template
void DList::insert(T elem, int index) // 向index位置插入
{
if(index <= 0) // 索引小于等于0都插在位置0
{
this.push_front(elem);
return;
}
else if(index >= cnt) // 索引大于等于cnt都插在末尾
{
this.push_back(elem);
return;
}
DNode *ptr = head;
int i = index;
while(i--)
{
ptr = ptr->next;
}
DNode *p = new DNode;
p->data = elem;
p->next = ptr->next; // 右手牵i结点
p->previous = ptr; // 左手牵i-1结点
ptr->next->previous = p; // i-1分别牵p结点
ptr->next = p; // i结点牵p
cnt++;
} 4. 任意位置删除(del)
假设我们要删除元素i,那么我们就需要将元素i的前置和后置结点“牵手”,抛弃i结点,然后释放内存。与单链表不同的是,改变i-1结点的next域后,假如存在i+1结点,还需要将i+1结点的previous域置为i-1。如果删除的元素是最后一个的话,同样,需要移动尾指针 。
注意!我!不!想!画!图!了!!!能把Windows画图软件用的这么6的,也只有我了吧哈哈哈。
这里我们只要注意下指针域的完整就可以了,直接上代码,步骤我在注释里,大家可以凭借高超的想象力,参考单链表的图自行在脑海中绘图:
template
void DList::del(int index) // 删除index位置的元素
{
if(index < 0 || index >= cnt)
{
return;
}
DNode *ptr = head;
int i = index;
while(i--)
{
ptr = ptr->next;
}
DNode *p = ptr->next; // 获取待删元素指针
ptr->next = p->next;
if(p->next != NULL) // 待删元素不是最后一个
{
p->next->previous = ptr;
}
delete p;
if(index == cnt - 1) // 如果删除的元素是最后一个
{
tail = ptr; // 修改尾指针指向为ptr(删除元素的前置)
}
cnt--;
} 5. 获取任意索引位置元素指针(get)
同单链表,没什么特别的地方,初始化一个指针ptr指向head->next,循环index次即可,注意判断溢出的index。
代码:
template
DNode* DList::get(int index) // 获取index位置的元素指针
{
if(index >= cnt) // 如果给定位置过大,则默认返回最后元素
{
index = cnt - 1;
}
if(index < 0) // 如果给定位置过小,则默认返回首元素
{
index = 0;
}
int i = index;
DNode *ptr = head->next; // 指针指向首元素
while(i--)
{
ptr = ptr->next;
}
return ptr;
} 6. 获取指定元素第一次出现的元素指针(find)
这里是新添的一个功能,我让它的返回值是指针,大家也可以修改代码让其返回索引(重载一个也行),总之大家想怎么写就这么写,这里只是参考,由于这里是根据元素值查找元素所在位置,所以我们需要遍历整个链表,遇到匹配元素就返回指针,如果到了链表尾还未找到,直接返回NULL。
代码如下:
template
DNode* DList::find(T elem) // 获取elem第一次出现的位置的元素指针
{
DNode *ptr = head->next;
while(ptr)
{
if(ptr->data == elem)
{
// 找到匹配元素,跳出循环,ptr指向该元素
break;
}
ptr = ptr->next;
}
// 循环正常结束说明未找到,此时ptr==NULL
return ptr;
} 7. 获取链表大小(size)
直接返回私有字段cnt,其实就是个getter啊,没啥好说的,代码:
template
int DList::size() // 获取链表的大小
{
return cnt;
} 8. 遍历链表(each)
这个遍历链表我添加了一个参数,因为是双向链表,单向遍历体现不出它的优势,所以加了个参数让它可以双向遍历,method为0时正向遍历,为1或其他值时反向遍历,默认为0。需要注意的是,我们正向遍历的结束点是指针为空时结束,而反向遍历却不是,为啥呢?别忘了我们有头结点!所以反向遍历的结束标志是head!下面给出起点终点。
正向:head->next ===> NULL
反向:tail ===> head
多说无益,看代码理解:
template
void DList::each(char split, int method = 0) // 遍历输出链表,以split参数为间隔,method为0正向,为1反向,默认0
{
// 根据method初始化遍历的起点
DNode *p = method ? tail : head->next;
while(p && p != head) // 结束条件: p为NULL,即到达链表尾;或者p等于head,即到达链表头
{
cout<<(p->data);
p = method ? p->previous : p->next; // 根据method决定游标指针的移动方向
putchar(p == NULL || p == head ? '\n' : split); // 输出换行或分隔符
}
} **完整版双向链表代码,附测试用例
#include
using namespace std;
template
struct DNode
{
T data;
DNode *next, *previous;
};
template
class DList
{
private:
DNode *head, *tail;
int cnt;
public:
DList()
{
head = new DNode;
tail = head;
head->next = NULL;
head->previous = NULL;
cnt = 0;
}
void push_back(T elem); // 尾部插入
void push_front(T elem); // 头部插入
void insert(T elem, int index); // 向index位置插入
void del(int index); // 删除index位置的元素
DNode* get(int index); // 获取index位置的元素指针
DNode* find(T elem); // 获取elem第一次出现的位置的元素指针
int size(); // 获取链表的大小
void each(char split, int method); // 遍历输出链表,以split参数为间隔,method为0正向,为1反向,默认0
};
template
void DList::push_back(T elem) // 尾部插入
{
DNode *p = new DNode;
p->data = elem;
p->next = NULL;
p->previous = tail;
tail->next = p;
tail = p;
cnt++;
}
template
void DList::push_front(T elem) // 头部插入
{
DNode *p = new DNode;
p->data = elem;
p->next = head->next; // 右手牵着head的next
p->previous = head; // 左手牵着head
if(head->next != NULL) // head后有结点
{
head->next->previous = p; // head后置结点的前置结点改为p
}
head->next = p;
if(cnt == 0) // 无元素,移动尾指针
{
tail = p;
}
cnt++;
}
template
void DList::insert(T elem, int index) // 向index位置插入
{
if(index <= 0) // 索引小于等于0都插在位置0
{
this.push_front(elem);
return;
}
else if(index >= cnt) // 索引大于等于cnt都插在末尾
{
this.push_back(elem);
return;
}
DNode *ptr = head;
int i = index;
while(i--)
{
ptr = ptr->next;
}
DNode *p = new DNode;
p->data = elem;
p->next = ptr->next; // 右手牵i结点
p->previous = ptr; // 左手牵i-1结点
ptr->next->previous = p; // i-1分别牵p结点
ptr->next = p; // i结点牵p
cnt++;
}
template
void DList::del(int index) // 删除index位置的元素
{
if(index < 0 || index >= cnt) // 非法位置,忽略
{
return;
}
DNode *ptr = head;
int i = index;
while(i--)
{
ptr = ptr->next;
}
DNode *p = ptr->next; // 获取待删元素指针
ptr->next = p->next;
if(p->next != NULL) // 待删元素不是最后一个
{
p->next->previous = ptr;
}
delete p;
if(index == cnt - 1) // 如果删除的元素是最后一个
{
tail = ptr; // 修改尾指针指向为ptr(删除元素的前置)
}
cnt--;
}
template
DNode* DList::get(int index) // 获取index位置的元素指针
{
if(index >= cnt) // 如果给定位置过大,则默认返回最后元素
{
index = cnt - 1;
}
if(index < 0) // 如果给定位置过小,则默认返回首元素
{
index = 0;
}
int i = index;
DNode *ptr = head->next; // 指针指向首元素
while(i--)
{
ptr = ptr->next;
}
return ptr;
}
template
DNode* DList::find(T elem) // 获取elem第一次出现的位置的元素指针
{
DNode *ptr = head->next;
while(ptr)
{
if(ptr->data == elem)
{
// 找到匹配元素,跳出循环,ptr指向该元素
break;
}
ptr = ptr->next;
}
// 循环正常结束说明未找到,此时ptr==NULL
return ptr;
}
template
int DList::size() // 获取链表的大小
{
return cnt;
}
template
void DList::each(char split, int method = 0) // 遍历输出链表,以split参数为间隔,method为0正向,为1反向,默认0
{
// 根据method初始化遍历的起点
DNode *p = method ? tail : head->next;
while(p && p != head) // 结束条件: p为NULL,即到达链表尾;或者p等于head,即到达链表头
{
cout<<(p->data);
p = method ? p->previous : p->next; // 根据method决定游标指针的移动方向
putchar(p == NULL || p == head ? '\n' : split); // 输出换行或分隔符
}
}
int main()
{
DList lst;
lst.push_front(1);
lst.each(' ');
lst.push_back(2);
lst.each(' ');
lst.push_front(0);
lst.each(' ');
lst.each(' ', 1);
lst.del(1);
lst.each(' ');
lst.get(0)->data = 233;
lst.find(2)->data = 666;
lst.each(' ');
return 0;
}
SDUT OJ 2054 数据结构实验之链表九:双向链表
好啦,双向链表就讲完了,是不是跟单链表很像?确实很像,只要学会了单链表,双向链表也不在话下,只要注意指针的细节处理就好。
本章内容结束,欢迎继续交流学习~
下集预告&传送门:数据结构与算法专题之线性表——链表(三)循环链表