pytorch-LSTM中参数计算以及输出分析

参数计算

---

  首先这篇博客不是介绍LSTM原理的，因为我也不敢说我已经完全理解了LSTM。。。。。。好了，言归正传，我们开始计算lstm中的参数，首先来看pytorch中公式怎么写的：
$$\begin{array}{llcc}& & & \\ & {\mathbf{i}}_{\mathbf{t}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{i}\mathbf{i}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}_{\mathbf{i}\mathbf{i}}+{\mathbf{W}}_{\mathbf{h}\mathbf{i}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}_{\mathbf{h}\mathbf{i}})& & (1)\\ & & & \\ & {\mathbf{f}}_{\mathbf{t}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{i}\mathbf{f}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}_{\mathbf{i}\mathbf{f}}+{\mathbf{W}}_{\mathbf{h}\mathbf{f}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}_{\mathbf{h}\mathbf{f}})& & (2)\\ & & & \\ & {\mathbf{g}}_{\mathbf{t}}=\tanh ({\mathbf{W}}_{\mathbf{i}\mathbf{g}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}_{\mathbf{i}\mathbf{g}}+{\mathbf{W}}_{\mathbf{h}\mathbf{g}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}_{\mathbf{h}\mathbf{g}})& & (3)\\ & & & \\ & {\mathbf{o}}_{\mathbf{t}}=\mathbf{\sigma }({\mathbf{W}}_{\mathbf{i}\mathbf{o}}{\mathbf{x}}_{\mathbf{t}}+{\mathbf{b}}_{\mathbf{i}\mathbf{o}}+{\mathbf{W}}_{\mathbf{h}\mathbf{o}}{\mathbf{h}}_{\mathbf{t}-1}+{\mathbf{b}}_{\mathbf{h}\mathbf{o}})& & (4)\\ & & & \\ & {\mathbf{c}}_{\mathbf{t}}={\mathbf{f}}_{\mathbf{t}}\ast {\mathbf{c}}_{\mathbf{t}-1}+{\mathbf{i}}_{\mathbf{t}}\ast {\mathbf{g}}_{\mathbf{t}}& & (5)\\ & & & \\ & {\mathbf{h}}_{\mathbf{t}}={\mathbf{o}}_{\mathbf{t}}\ast \tanh ({\mathbf{c}}_{\mathbf{t}})& & (6)\end{array}$$
  这里需要注意的是pytorch没有采用拼接的方法将$x和h$进行拼接，而是分开计算，同时每个公式多了一个偏置。 当然,这都无关紧要了。这里我们假设input_size=100, hidden_size=100 代码如下：

rnn=nn.LSTM(input_size=100,hidden_size=100,num_layers=1,bidirectional=False)
for p in rnn.parameters():
    print(p.size())

output：
torch.Size([400, 100])
torch.Size([400, 100])
torch.Size([400])
torch.Size([400])

  接下来我们来看这个参数是怎么计算来的。首先我们要明确一点就是我们要计算的参数是什么，我们要计算的参数是 $w,b$。我们知道LSTM中有三个门控制单元和一个输入单元，他们的的参数大小是一样的，所以只需要计算一个然后乘以4就行了。如果对LSTM不熟悉也可以从上面的公式里看出一共8对$w,b$.首先我们知道 $x$ 是一个100维的向量，看公式：(1) 我们知道经过 $sigmoid$ 之后应该也是100维的向量那么从而可以推断出 $Wx$ 也是100维喽。那么我们就可以得到：

$$\mathbf{W}[100\ast 100]\ast \mathbf{x}[100\ast 1]=[100\ast 1]\text{\hspace{1em}(7)}$$

  这样就得到了 $W$ 大小啦 $b$ 的大小同样可以推断出 $b$ 是100维啦。然而会有人疑问输出明明是 [400 * 100] 而不是[100 * 100]我们观察上面LSTM的前四个公式是不是一共八个 $W$ ，左边四个，右边四个，嗯，没错 [400 * 100] 就是分别代表左边四个 $W$ 的总大小，当然，[400]也就是对应的b的大小了。这里一共 40000+40000+800=80800 个参数

---

注意 1

---

  另外说一点就是其他的博客有通过公式：$4(mn+n^2+n)$ 来计算总参数，其中 m 是 input_size，n 是 hidden_size.对应我们上面例子就是 m=n=100 然后计算出 80400 个参数。为什么和上面的不一样呢。其实是一样的，我在开头也说了，pytorch 没有采用拼接的方法，并且每个公式多处一个偏置也就是一共多出 4 个。一个 100 维度也就是 400 个参数。嗯，到这里计算结束了。

---

注意 2

---

  当网络是双层或者双向时，只需要把参数乘以2即可，但是这里要注意的是，当网络为双层双向时就需要注意了。废话不多说先看代码效果好吧，代码如下：

rnn=nn.LSTM(input_size=100,hidden_size=100,num_layers=2,bidirectional=True)
for p in rnn.parameters():
    print(p.size())
output:
torch.Size([400, 100])
torch.Size([400, 100])
torch.Size([400])
torch.Size([400])
torch.Size([400, 100])
torch.Size([400, 100])
torch.Size([400])
torch.Size([400])
torch.Size([400, 200])
torch.Size([400, 100])
torch.Size([400])
torch.Size([400])
torch.Size([400, 200])
torch.Size([400, 100])
torch.Size([400])
torch.Size([400])

  不知道大家注意到了没有倒数第四行和倒数第八行是[400 * 200],为什么会这样呢? 接下来，我先从pytorch给出的公式来解释，我们在计算第二层的时候其实输入x已经变了，变成多少维呢，没错是200维，forward+backward 这样，我上面说了pytorch没有采用$x,h$拼接的方式计算而是采用分开计算，那么先来看$x$喽，我们已经知道x的维度维200 * 1，而我们想得到的输出是100那么我们就需要一个满足这个等式：

$${\mathbf{W}}_{\mathbf{i}}[100\ast 200]\ast \mathbf{x}[200\ast 1]=[100\ast 1]\text{\hspace{1em}(8)}$$

  我们可以看出 $W_i$ 是[100 * 200]。好了，接着我们来看 $h，h$ 还是100维的这个是hidden_size决定的。同样的我们计算出符合等式：

$${\mathbf{W}}_{\mathbf{h}}[100\ast 100]\ast \mathbf{h}[100\ast 1]=[100\ast 1]\text{\hspace{1em}(9)}$$

  这样 $W_h$ 也就出来了为[100 * 100]
  好了分析了半天，计算总数吧，左边的 $W$ 也就是 $W_i$ 为[100 * 200] * 4 =80000 再加上$b$[100] * 4=400,嗯，左边一共是80400个参数，右边是 [100 * 100]* 4 + [100] * 4=40400.左边和右边加起来就是 120800 个参数。我们来用公式检验一下：m=200，n=100， (200 * 100+100 * 100+100)*4=120400, 至于差的400和上面的解释一样是差在 $b$ 上。

---

输出分析

---

看完下面的分析会对上面的理解更加清晰：
首先，看看输入的数据的格式
output：( batch,seq_len, input_size)
h0/c0：(num_layers * num_directions, batch, hidden_size)

这个是数据的输入的格式：这里需要注意的是这里使用的是batch_first=True;
网络的输出和输入大小差不多（主要是output的差别）；
输出是：
output：(seq_len, batch, num_directions * hidden_size)
hn/cn：(num_layers * num_directions, batch, hidden_size)
这里解释一下：
output：保存每个batch最后一层的各个time_step的输出；
hn：保存的是每个batch的每一层的最后一个time_step的输出；
cn和hn类似只是保存的是c值。
看下图会更清楚：

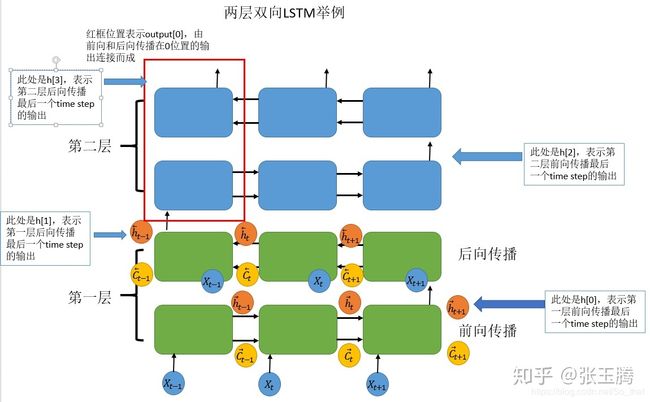
参看下面程序：

import torch
import torch.nn as nn
bilstm = nn.LSTM(input_size=10, hidden_size=20, num_layers=2, bidirectional=True,batch_first=True)
'''batch:5 seq_len:3 dim:10 '''
input = torch.randn(5, 3, 10)
'''(num_layers * num_directions, batch, hidden_size)'''
h0 = torch.randn(4, 5, 20)
'''(num_layers * num_directions, batch, hidden_size)'''
c0 = torch.randn(4, 5, 20)
output, (hn, cn) = bilstm(input, (h0, c0))
print('output shape: ', output.shape)
print('hn shape: ', hn.shape)
print('cn shape: ', cn.shape)

print(output[4, 2, :20])
print(output[4, 0, 20:])
print(hn[2, 4,:])
print(hn[3, 4,:])
output:
output shape:  torch.Size([5, 3, 40])
hn shape:  torch.Size([4, 5, 20])
cn shape:  torch.Size([4, 5, 20])
tensor([-0.0395, -0.2433, -0.0611,  0.0162, -0.1448, -0.0356, -0.0575,  0.0237,
         0.0697, -0.0294, -0.0441, -0.0093,  0.0053,  0.0195,  0.1096, -0.0940,
         0.0843, -0.0435,  0.0702, -0.0798], grad_fn=<SliceBackward>)
tensor([ 0.0555, -0.1071,  0.0042, -0.0060, -0.0502,  0.0296,  0.1325, -0.3112,
         0.1473, -0.1250,  0.0804, -0.0464,  0.0957,  0.1257,  0.0913,  0.0027,
        -0.0442,  0.1325, -0.2190, -0.0221], grad_fn=<SliceBackward>)
tensor([-0.0395, -0.2433, -0.0611,  0.0162, -0.1448, -0.0356, -0.0575,  0.0237,
         0.0697, -0.0294, -0.0441, -0.0093,  0.0053,  0.0195,  0.1096, -0.0940,
         0.0843, -0.0435,  0.0702, -0.0798], grad_fn=<SliceBackward>)
tensor([ 0.0555, -0.1071,  0.0042, -0.0060, -0.0502,  0.0296,  0.1325, -0.3112,
         0.1473, -0.1250,  0.0804, -0.0464,  0.0957,  0.1257,  0.0913,  0.0027,
        -0.0442,  0.1325, -0.2190, -0.0221], grad_fn=<SliceBackward>)

上面这个程序的最后的输出的意思是这样的：
第一个输出：output[4, 2, :20] 代表batch=5，seq=3，：20 代表前向传播结果。
第三个输出：hn[2, 4,:]：2代表，第二层（也就是最后一层）的前向传播结果；4，代表batch=5，
从结果可以看出来这两个是一样的。
二四同理。

---

参考

https://zhuanlan.zhihu.com/p/39191116